Crystals of Time
Spontaneous symmetry breaking is ubiquitous in nature. It occurs when the ground state (classically, the lowest energy state) of a system is less symmetrical than the equations governing the system. Examples in which the symmetry is broken in excited states are common—one just needs to think of Kepler’s elliptical orbits, which break the spherical symmetry of the gravitational force. But spontaneous symmetry breaking refers instead to a symmetry broken by the lowest energy state of a system. Well-known examples are the Higgs boson (due to the breaking of gauge symmetries), ferromagnets and antiferromagnets, liquid crystals, and superconductors. While most examples come from the quantum world, spontaneous symmetry breaking can also occur in classical systems [1].
Three articles in Physical Review Letters investigate a fascinating manifestation of spontaneous symmetry breaking: the possibility of realizing time crystals, structures whose lowest-energy states are periodic in time, much like ordinary crystals are periodic in space. Alfred Shapere at the University of Kentucky, Lexington, and Frank Wilczek at the Massachusetts Institute of Technology, Cambridge [2], provide the theoretical demonstration that classical time crystals can exist and, in a separate paper, Wilczek [3] extends these ideas to quantum time crystals. Tongcang Li at the University of California, Berkeley, and colleagues [4] propose an experimental realization of quantum time crystals with cold ions trapped in a cylindrical potential.
In nature, the most common manifestation of spontaneous symmetry breaking is the existence of crystals. Here continuous translational symmetry in space is broken and replaced by the discrete symmetry of the periodic crystal. Since we have gotten used to considering space and time on equal footing, one may ask whether crystalline periodicity can also occur in the dimension of time. Put differently, can time crystals—systems with time-periodic ground states that break translational time symmetry—exist? This is precisely the question asked by Alfred Shapere and Frank Wilczek.
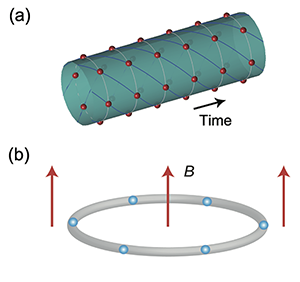
How can one create a time crystal? The key idea of the authors, both for the classical and quantum case, is to search for systems that are spatially ordered and move perpetually in their ground state in an oscillatory or rotational way, as shown in Fig. 1. In the time domain, the system will periodically return to the same initial state.
Consider first the classical case. At first glance, it may seem impossible to find a system in which the lowest-energy state exhibits periodic motion: in classical mechanics the energy minimum is normally found for vanishing derivatives of positions (velocities) and momenta. However, Shapere and Wilczek [2] find a mathematical way out of this impasse. Assuming a nonlinear relation between velocity and momentum, they show that the energy can become a multivalued function of momentum with cusp singularities, with a minimum at nonzero velocities. While this provides a mathematical solution for creating classical time crystals, the authors fall short of identifying candidate systems. It remains to be seen if such an exotic velocity-momentum relation can be engineered in a real system.
For once, the quantum case seems to be easier than its classical counterpart. A number of familiar quantum phenomena almost do the trick, resulting in systems that rotate or oscillate in their lowest energy state. Wilczek suggests the example of a supercoducting ring, which can support a permanent current in its ground state under proper conditions. An even closer analogy can be found in a continuous wave laser. Spontaneous symmetry breaking makes the electric-field amplitude oscillate in time with a well-defined phase [5], almost creating a photonic time crystal. Yet in these systems—so close to being quantum crystals—a key element is missing: the persistent superconducting current and the laser light intensity are constant, not periodically varying, and the translational symmetry in time is not broken. How can one then add time periodicity to a quantum system?
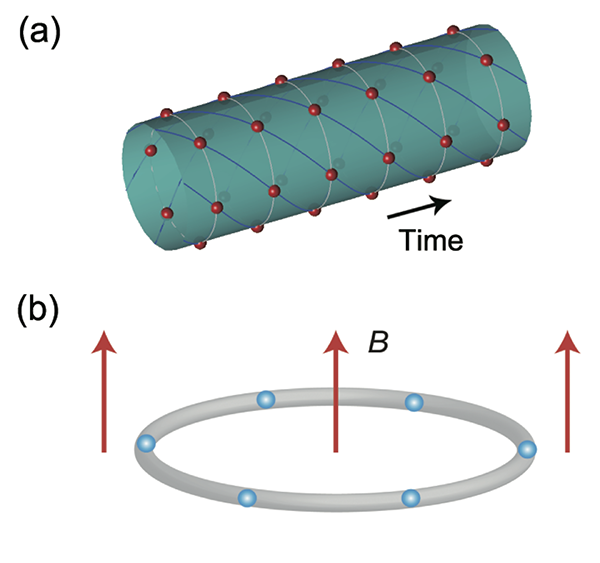
Wilczek argues that this could be done in a system of quantum particles moving along a ring by introducing a mechanism that localizes them. If moving particles can be made to group in ordered “lumps,” this would naturally result in temporal periodicity as such lumps travel in a circle. Consider a ring filled with a large number of bosons with attractive interactions between them. If the system is isolated, its ground state is a symmetric state of constant density along the ring. But such a state is fragile: any interaction with the environment or any measurement (e.g., the determination of the position of an individual particle) makes the system collapse into a well-localized state along the ring, causing spontaneous symmetry breaking in space. Such localization can form a so-called soliton [6], a solution of the nonlinear Schrödinger equation that describes such a system. Wilczek’s insight is that an applied magnetic field, perpendicular to the ring, will cause the soliton to move. The resulting periodic motion would create a time crystal.
Wilczek does not address the problem of how to engineer such a system. But possible simple solutions come to mind. One could use cold neutral atoms with weak mutual attraction and exploit atom-laser interactions to create forces that mimic a magnetic field. Such a scheme to create an artificial effective magnetic field has been already realized in the laboratory [7]. An even simpler possibility is to stir an atomic ensemble while it is cooled towards Bose-Einstein condensation in an appropriate ring-shaped trap. Indeed, a stirring laser beam was previously used to create vortices in a condensate held in a magnetic trap [8]. Here, the stirring laser would introduce a rotation into the system, driving the soliton’s movement.
The article by Li et al. [4] provides the detailed description of an experiment that seems to be feasible. The scheme is based on beryllium ions trapped in a ring-shaped potential at nanokelvin temperatures. As a consequence of mutual Coulomb repulsion, the ions arrange periodically in space, forming a ring crystal. Similar geometries have already been demonstrated by the group of David Wineland [9]. Li and co-workers show that the addition of a weak magnetic field perpendicular to the ring would lead to the rotation of the spatially periodic ring crystal structure, thus creating a time crystal. Similarly to Wilczek’s model, spontaneous symmetry breaking of the rotational degree of freedom, through circular movement, is translated into breaking of translational time invariance.
Time crystals may sound dangerously close to a perpetual motion machine, but it is worth emphasizing one key difference: while time crystals would indeed move periodically in an eternal loop, rotation occurs in the ground state, with no work being carried out nor any usable energy being extracted from the system. Finding time crystals would not amount to a violation of well-established principles of thermodynamics. If they can be created, time crystals may have intriguing applications, from precise timekeeping to the simulation of ground states in quantum computing schemes. But they may be much more than advanced devices. Could the postulated cyclic evolution of the Universe be seen as a manifestation of spontaneous symmetry breaking akin to that of a time crystal? If so, who is the observer inducing—by a measurement—the breaking of the symmetry of time?
References
- F. Strocchi, Symmetry breaking, Lecture Notes in Physics (Springer, Heidelberg, 2008)[Amazon][WorldCat]
- A. Shapere and F. Wilczek, “Classical Time Crystals,” Phys. Rev. Lett. 109, 160402 (2012)
- F. Wilczek, “Quantum Time Crystals,” Phys. Rev. Lett. 109, 160401 (2012)
- T. Li, Z-X. Gong, Z-Q. Yin, H. T. Quan, X. Yin, P. Zhang, L-M. Duan, and X. Zhang, “Space-Time Crystals of Trapped Ions,” Phys. Rev. Lett. 109, 163001 (2012)
- H. Haken, Synergetics: An Introduction (Springer-Verlag, Berlin, 1977)[Amazon][WorldCat]
- R. Kanamoto, H. Saito, and M. Ueda, ”Critical Fluctuations in a Soliton Formation of Attractive Bose-Einstein Condensates,” Phys. Rev. A 73, 033611 (2006)
- Y.-J. Lin, R. L. Compton, K. Jiménez-García, J. V. Porto, and I. B. Spielman, “Synthetic Magnetic Fields for Ultracold Neutral Atoms,” Nature 462, 628 (2009)
- K. W. Madison, F. Chevy, W. Wohlleben, and J. Dalibard, “Vortex Formation in a Stirred Bose-Einstein Condensate,” Phys. Rev. Lett. 84, 806 (2000)
- M. G. Raizen, J. M. Gilligan, J. C. Bergquist, W. M. Itano, and D. J. Wineland, “Ionic Crystals in a Linear Paul trap,” Phys. Rev. A 45, 6493 (1992)