Multiferroic Propellers

Maxim Mostovoy

Viewpoint

Multiferroic Propellers

Maxim Mostovoy

Zernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, Groningen 9747 AG, The Netherlands

February 6, 2012• Physics 5, 16

Helicoidal magnetic order induces a record high electrical polarization.

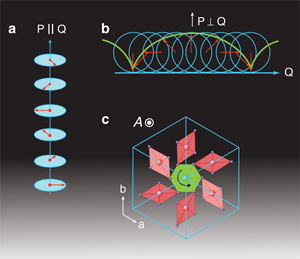
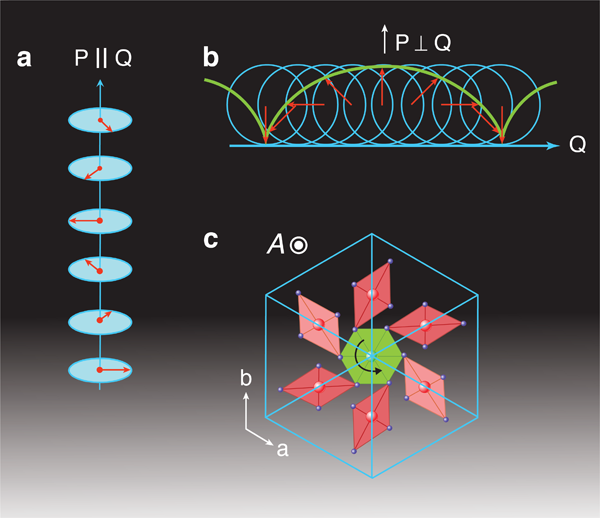
Figure caption — **Figure 1:** (a) Helicoidal spin spiral in which the spin rotation axis and the induced polarization are parallel to the spiral wave vector. (b) Cycloidal spin spiral in which spins (red arrows) rotate around an axis normal to the spiral wave vector Q. The induced electric polarization P is normal to both the wave vector and the spin rotation axis. Green curve is the cyloid. (c) Propellerlike structure of $Mn$ - $O$ octahedra in ${CaMn}_{7} O_{12}$ , which changes the rotation direction when the sample is turned around.

Control of spin ordering in magnetic insulators with an applied electric field (also known as the magnetoelectric effect) can significantly reduce the power consumption of memory devices, but with no mobile charges present, it would seem to be an impossible task. Encouragingly, it was recently discovered that some magnetic orders induce an electric polarization, which couples spins to electric field. So far, the electrical polarization in such magnetic ferroelectrics (also called multiferroics) tends to be small and the Néel magnetic transition temperature is usually well below liquid nitrogen temperature. Now, however, Roger Johnson and co-workers at the University of Oxford, UK, with collaborators in France, report in Physical Review Letters on achieving giant polarization in ${CaMn}_{7} O_{12}$ . The measured polarization is the highest measured magnetically induced polarization, persisting up to a Néel temperature of $90 K$ . Remarkably, this polarization appears to be induced by a long-period helicoidal (or proper-screw) spin spiral [see Fig. 1(a)], in which spins rotate around the spiral wave vector [1]. This discovery represents an important development for the field of magnetic ferroelectrics, as large polarization is crucial for electric manipulation of spins. It confirms earlier estimates of polarization from studies of polycrystalline samples [2].

The most ubiquitous spin ordering that gives rise to ferroelectricity is the cycloidal spiral, in which spins rotate around an axis normal to the spiral wave vector. A cycloid—a curve traced by a point on the rim of a wheel rolling over a flat surface—is asymmetric along the direction normal to both the direction of motion and the wheel axis, and this is also the direction of the electric polarization induced by a spin cycloid [see Fig. 1(b)]. By contrast, helicoidal ferroelectrics are rare, and all materials studied so far are only weakly ferroelectric [3,4].

The clockwise or counterclockwise direction of spin rotation in the helicoidal spiral is described by a quantity called helicity. This quantity changes sign under inversion of all spatial coordinates and is the reason why, in magnets without inversion symmetry, spins often roll into a spiral. The sign of helicity is imposed by the crystal structure. The ${CaMn}_{7} O_{12}$ crystals are, however, symmetric under inversion, and the positive or negative helicity is chosen spontaneously at the magnetic transition point. The direction of the electric polarization, which is set at the same transition temperature as the magnetic transition temperature, is determined by the direction of spin rotation in the spiral.

One would think it is impossible to couple electric polarization to helicity because the direction of spin rotation in the helical spiral is preserved when the spiral axis is rotated, whereas the polarization vector oriented along the axis of the helix changes sign when the sample is turned around. The only way to make the electric polarization proportional to helicity is to “forbid” such crystal rotations, that is, the crystal should look different when viewed from above and from below [5]. Johnson and colleagues suggest that this can be a result of an axial lattice distortion transforming like a component of an axial vector, which remains invariant under inversion and rotations around the helical axis, but changes sign when this axis is turned around. The authors show that in ${CaMn}_{7} O_{12}$ , the axial vector is induced by the “propellerlike” structure formed by the manganese-oxygen octahedra in each unit cell [see Fig. 1(c)]. The product of this axial vector and helicity can be linearly coupled to electric polarization. The fact that the helical spiral induces electric polarization only in axial crystals also explains why the helicoidal ferroelectrics are less common than the cycloidal ones.

But while the relation between helicity, axiality, and ferroelectricity may now be clear, why is the polarization of ${CaMn}_{7} O_{12}$ so much larger than other helicoidal ferroelectrics? The form of the magnetoelectric coupling for the helicoidal spiral, and the fact that it is incommensurate with the crystal lattice (the period of the helix is not a multiple of the lattice constant), points at the important role of the electron spin-orbit coupling. Due to this coupling, a pair of noncollinear spins pushes positively and negatively charged ions away from each other. The resulting electric dipole is typically rather small because the spin-orbit coupling is a weak relativistic effect for most magnetic materials, which makes one wonder why the polarization of ${CaMn}_{7} O_{12}$ is 5 times larger than that of ${TbMnO}_{3}$ with a cylcoidal spiral ordering? In addition, the spin noncollinearity in ${CaMn}_{7} O_{12}$ is very small: the angle between neighboring spins along the helix axis is only $4$ degrees.

The case is clearly not yet settled. To introduce electric dipoles, the most efficient route is by pairs of collinear spins, which requires no relativistic interactions. However, this mechanism usually only works if magnetic modulation is commensurate with the lattice and it is not effective in spirals. This suggests an alternative interpretation of the origin of ferroelectricity in ${CaMn}_{7} O_{12}$ . It turns out that the crystal lattice of this material also shows a small periodic incommensurate modulation below $250 K$ , and the period of the magnetic ordering appearing below $90 K$ equals two periods of the structural modulation [6]. This situation is reminiscent of stripes—atomic-scale rivulets of charge in the $Cu$ - $O$ plane in high-temperature cuprate superconductors—in which the antiferromagnetic spin order changes sign when it crosses a charged stripe. Below $55 K$ , neutron powder diffraction data indicate the existence of two different incommensurate magnetic modulations, and it turns out that the sum of their wave vectors equals the wave vector of the structural distortion. It seems this “synchronization” of structural and magnetic modulations enables the stronger nonrelativistic mechanism of magnetoelectric coupling. Further studies of magnetic states in this material are necessary to clarify the origin of its remarkably large electric polarization. However, the strong magnetoelectric coupling found in ${CaMn}_{7} O_{12}$ will undoubtedly stimulate the search for other axial ferroelectrics to see if they too exhibit such a large polarization.

References

R. D. Johnson, L. C. Chapon, D. D. Khalyavin, P. Manuel, P. G. Radaelli, and C. Martin, Phys. Rev. Lett. 108, 067201 (2012)
G. Zhang, S. Dong, Z. Yan, Y. Guo, Q. Zhang, S. Yunoki, E. Dagotto, and J.-M. Liu, Phys. Rev. B 84, 174413 (2011)
T. Kimura, J. C. Lashley, and A. P. Ramirez, Phys. Rev. B 73, 220401 (2006)
M. Kenzelmann et al., Phys. Rev. Lett. 98, 267205 (2007)
T. Arima, J. Phys. Soc. Jpn. 76, 073702 (2007)
W. Slawinski, R. Przenioslo, I. Sosnowska, and M. Bieringer, J. Phys. Condens. Matter 22, 186001 (2010)

About the Author

Maxim Mostovoy is a condensed matter theorist with interests in magnetism, multiferroics, and strongly correlated systems. He received his Ph.D. in 1998 from the University of Groningen. He worked at the Max Planck Institute for Solid State Research (Stuttgart), was appointed to the Mercator professorship at the University of Cologne and held visiting positions at the Hahn-Meitner Institute (Berlin) and RIKEN (Wako, Saitama). He is currently an associate professor at the Zernike Institute for Advanced Materials (Groningen).