Metals Get an Awkward Cousin

Ribhu  K. Kaul

Viewpoint

Metals Get an Awkward Cousin

Department of Physics and Astronomy, University of Kentucky Lexington, KY 40506, USA

July 23, 2012• Physics 5, 82

A newly predicted state of matter is a simple theoretical example of a phase that conducts electricity but is not smoothly connected to our conventional model of metals.

Figure caption — **Figure 1:** The rewriting of the $c$ electron as a product of an $f$ fermion and $τ$ Ising spin. The “orthogonal metal” is the simplest theoretical example of a non-Fermi-liquid metal. While it appears to be an ordinary Fermi liquid in many measurements, its unique character is manifest in its single-electron spectrum.

The sustained excitement that fundamental discoveries in solid-state physics have generated for over a century originates, at least in part, from the amazing technological applications that society has found for crystalline materials that conduct electricity. This list of materials, collectively described as metals, began with the familiar crystals of atoms such as silver [1], but has come to include a growing number of complex synthetic materials [2], which conduct electricity like their simpler cousins, but in a manner that has vexed condensed-matter physicists for decades. In Physical Review B, Rahul Nandkishore at the Massachusetts Institute of Technology, Cambridge, and co-workers [3] report on the theoretical possibility of a new kind of conducting phase of matter they call an “orthogonal metal,” which may shed light on this exciting puzzle.

Very early on, quantum mechanics provided a simple way to understand how electrons moving in crystals can be either insulating (like in diamond) or metallic (like in gold). Neglecting electron-electron interactions completely, the solution of the one-particle Schrödinger equation in the periodic potential of a crystal has bands of allowed energies separated by bands of forbidden energies. There are, then, two classes of electronic structures: band insulators in which all the bands are either fully filled or fully occupied, and band metals in which at least one band is partially filled. Fully occupied or fully empty bands are electrically inert and it is the partially filled bands that endow metals with the characteristic property of electrical conduction. Including the interactions of electrons with each other and assuming that they are weak can improve upon the noninteracting picture of a band metal. This dressed-up version of the original noninteracting picture of metallicity is called a Fermi liquid. Despite the ad hoc assumption that the electron-electron interactions can be treated as a small perturbation, the Fermi-liquid picture makes a number of predictions that have been borne out in experiment. Hence, in the $20$ th century, it has enjoyed the status of being the exclusive paradigm used to interpret the low-temperature properties of metals [4].

But what if electron-electron interactions are too strong for the band theory to be a correct starting point? Towards the end of the first half of the $20$ th century, Neville Mott and others proposed that electrons in all crystals, driven by their interactions with each other, would eventually become insulating if the lattice spacing could artificially be made large enough [5]. It turns out that Mott’s picture was not a theorists’ pipe dream: there are hundreds of materials in which electron motion is inhibited completely by electron-electron interactions at low temperatures, resulting in insulating behavior. Such materials, called Mott insulators, can have exotic magnetic properties despite their inability to conduct electricity. The study of quantum and classical magnetism in Mott insulators has evolved into one of the hottest frontiers of both experimental and theoretical condensed-matter physics in recent decades [6].

Given the exciting many-body physics in Mott insulators, it is natural to ask whether new non-Fermi-liquid paradigms for metallic states can emerge from the complexity of electron-electron interactions. In this field, experiments are far ahead of theories. More than a decade ago, Greg Stewart compiled in excess of $50$ examples of metals that have properties that deviate from the Fermi-liquid phenomenology [7]. It is generally accepted that this behavior is a result of electron-electron interaction and perhaps disorder, but despite the high stakes, there is no universally accepted simple theory that describes it [8]. While explaining experimental observations is the ultimate goal of any theory, as a first step, simple theoretical models that have metallic ground states but do not fall into the Fermi-liquid/band theory approach are highly desirable.

Nandkishore et al. have provided us with a theoretical example of such a non-Fermi-liquid phase of matter, which they have christened the orthogonal metal. The name originates from the interesting property that the wave functions of the current-carrying fermions in this phase are orthogonal to the wave functions of the microscopic electrons; in contrast to the usual Fermi liquids where the two have a strong overlap. The orthogonality feature leads to a state of matter that conducts electricity much like an ordinary metal, but even so, has distinct and unusual spectral properties that earn it the title of a non-Fermi liquid. The most attractive feature of this new phase of matter is that the orthogonal metal is perhaps the simplest theoretical example of a non-Fermi-liquid metal yet known.

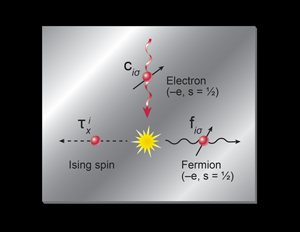
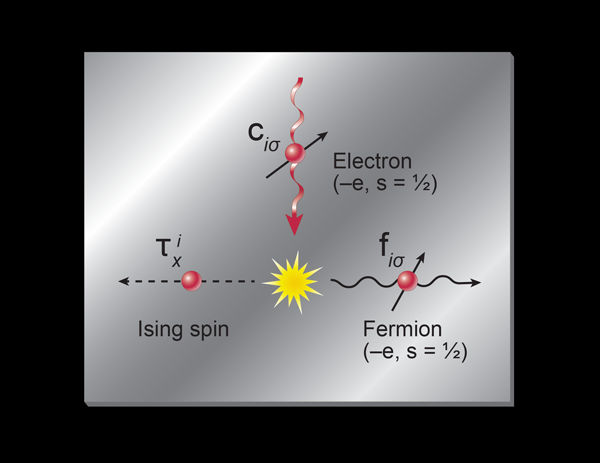
Technically, one procedure to access the orthogonal metal phase (see Fig. 1) is by writing the microscopic lattice electron operator $c_{i σ}$ on the site $i$ of a lattice as a product of a fermion operator $f_{i σ}$ and an Ising spin $τ_{i}^{x}$ ,

This rewriting of the $c$ electron operator supplemented by a local constraint on the $f$ and $τ$ degrees of freedom is referred to as the slave spin construction. It is an efficient way to access unconventional phases of the electrons, beginning with well-understood phases of the $f$ and $τ$ quanta. A central clue to the interpretation put forward in this work is that in the rewriting of the electron of Eq. (1), the $f$ fermions carry both the electrical charge and spin of the electron. This finding has significant consequences for the phases that can be accessed in a simple manner in the new representation, since it implies that in any phase in which the $f$ fermions form a metal, so will the microscopic $c$ electrons. Indeed, the authors show that the phase in which the $τ$ particle is condensed corresponds to a conventional Fermi liquid in which there is a finite overlap between the $f$ and the microscopic $c$ electrons. They then go on to show that when the $τ$ particles are disordered, one obtains the orthogonal metal in which the $f$ fermions have no overlap with the original microscopic $c$ electrons. The most striking feature of this new phase of matter is that it is compressible like an ordinary metal, yet its spectral function has a gap because of the orthogonality of the $c$ electron and the $f$ fermion.

The slave particle method is a convenient way to envision possible exotic phases of the $c$ electrons. However, a weakness of the slave particle approach is that it is unable to identify specific microscopic models of the $c$ electrons that realize the new phase. The authors address this important issue by providing exactly soluble toy quantum Hamiltonians in which the new phase is realized as a ground state. These exactly soluble models are not the typical generic Hamiltonians physicists would use to model condensed-matter systems, yet they provide important proof-of-principle examples that this new exotic phase can be stabilized in models with simple local interactions.

Looking forward, it is too early to judge how this theoretically proposed phase of matter will assist in the interpretation of the mysterious experimental data on the deviant metallic materials mentioned before. Its existence should certainly be kept in mind in looking for possible explanations of metals that display non-Fermi-liquid behavior. Detection may not always be obvious since outside of a few measurements that probe one-electron properties, such as photoemission and tunneling, orthogonal metals look like ordinary metals in most experiments. An intriguing, although admittedly optimistic, possibility is that we have already synthesized materials that are orthogonal metals, but have mistaken them for ordinary metals because of the subtle differences between these two phases! An immediate challenge for theoretical work is to find generic microscopic models of electrons that realize the orthogonal metal in their phase diagrams. To this end, the authors have provided variational wave functions as well as likely generic models that could realize this new phase. Recent advances in numerical methods for lattice Hamiltonians have allowed unbiased studies of many new models that harbor exotic critical points and phases [9], making one optimistic that the existence of orthogonal metals can be convincingly demonstrated in a generic model in the near future. It is clearly an exciting direction for future computational and experimental work to find for the new orthogonal metal a path from exotica to the catalog of standard condensed-matter phases.

Acknowledgment

This work was supported in part by NSF DMR-1056536.

References

N. W. Ashcroft and N. D. Mermin, Solid State Physics (Holt, Rinehart and Winston, New York, 1976)[Amazon][WorldCat]
One well known example material that harbors such behavior is the copper based superconductor, La{2−x}Sr{x}CuO{4}, above its critical temperature. For an overview, see A. J. Schofield, “Non-Fermi Liquids,” Contemp. Phys. 40, 95 (1999)
R. Nandkishore, M. A. Metlitski, and T. Senthil, ”Orthogonal metals: The simplest non-Fermi liquids,” Phys. Rev. B 86, 045128 (2012)
A. A. Abrikosov, Fundamentals of the Theory of Metals (North-Holland, Amsterdam, 1988)[Amazon][WorldCat]
N. Mott, Metal-Insulator Transitions (Taylor and Francis, New York, 1990)[Amazon][WorldCat]
L. Balents, “Spin Liquids in Frustrated Magnets,” Nature 464, 199 (2010)
G. R. Stewart, “Non-Fermi-Liquid Behavior in d- and f-electron Metals,” Rev. Mod. Phys. 73, 797855 (2001); “Addendum: Non-Fermi-Liquid Behavior in d- and f-electron Metals,” 78,743753 (2006)
Quantum criticality is a popular contender. For an interesting recent discussion see P. Coleman, “Quantum Criticality and Novel Phases: A Panel Discussion,” Phys. Status Solidi B 247,506 (2010)
R. K. Kaul, R. G. Melko, and A. W. Sandvik, “Bridging lattice-scale physics and continuum field theory with quantum Monte Carlo simulations,”arXiv:1204.5405v1; Annu. Rev. Cond. Matter Phys. (to be published)

About the Author

Ribhu Kaul is a professor of physics in the Department of Physics and Astronomy at the University of Kentucky. His research interests lie in the quantum many-body problem and its application to a wide variety of condensed-matter systems. He studied at St. Xaviers’ College, Cornell, and Duke and held postdoctoral positions at Harvard and Microsoft Station Q, before joining the University of Kentucky in 2010.