Thinking Inside the Box
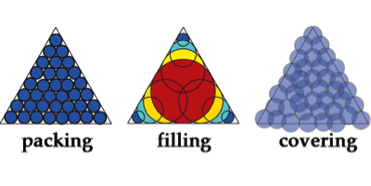
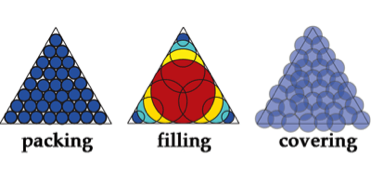
Deceptively simple questions like “How many gumballs fit in a box?” or “How many stamps does it take to cover an orange?” are at the heart of some really hard problems in applied mathematics; namely, the “packing problem” and the “covering problem.” Writing in Physical Review Letters, Carolyn Phillips at the University of Michigan, Ann Arbor, and colleagues take steps to tackle filling, a new optimization problem in between packing and covering.
A two-dimensional version of the question Phillips et al. address might be posed like this: Imagine you have a square window and you want to block out as much light as possible by taping some opaque circular tiles to the glass. You can use a mixture of tiles with any radius, and they can overlap with each other, but you only have money to buy five. As a general optimization problem, this amounts to asking “What is the best way to place overlapping circles (or, in D, spheres) of any size within a bounded area (volume) so as to fill it?”
The authors show that for a given shape, they only need to consider solutions where the circles or spheres lie on the shape’s medial axis—a linelike representation of the shape’s topology—and, as an example, present a numerical strategy for optimally filling D polygons with circles.
Phillips et al. became interested in the filling problem as a means to help them model interactions between nanoparticles, which can be approximated as rigid bodies of overlapping spheroids. But the work could, according to the authors, be applicable to computer animation, where graphic artists look for ways to describe complex shapes with a minimum of simple, overlapping volumes. – Jessica Thomas