The Life and Death of Cells
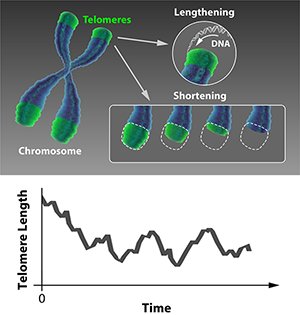
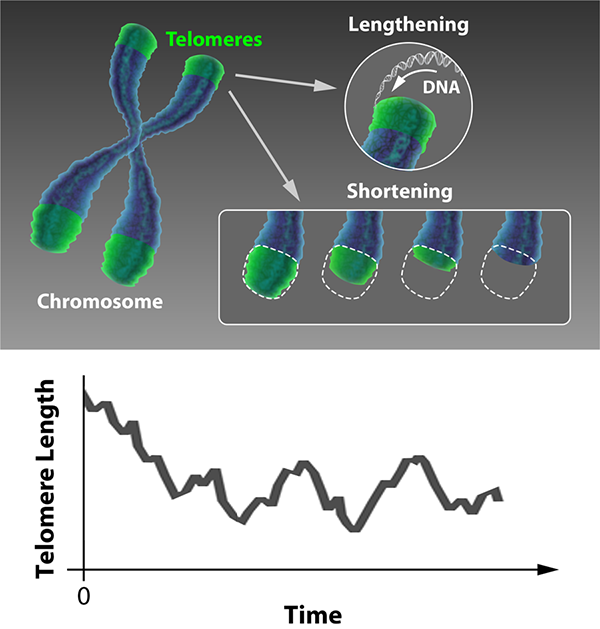
We may think of built-in obsolescence as a modern marketing trick, but biology got there first. Rather than being able to replicate indefinitely, most cells in our bodies divide only a finite number of times before they switch off. The aging of a cell (senescence) is the process of accumulative changes to its molecular structure that disrupt its function with time, leading to its degradation and death. A key factor in senescence is the shortening of the protective ends of a cell’s chromosomes, called telomeres. As reported in Physical Review Letters [1], Khanh Dao Duc and David Holcman at Ecole Normale Supérieure, France, have formulated a statistical mechanics model that describes how this process is regulated, providing a powerful method for predicting whether cells live or die.
Cell fate is dictated by the stability of the chromosomes. A source of instability is the fact that the ends of chromosomes may be indistinguishable from a break in double-stranded DNA. If a naked chromosome end is detected, the cell mistakenly activates a sophisticated DNA repair mechanism that stitches the apparently broken DNA together, resulting in unwanted chromosome fusion that then prevents faithful replication of the genetic material. What normally prevents this are the short stretches of stabilizing DNA called telomeres that protect the ends of the chromosomes. However, as you age and your cells divide to regenerate tissues, the telomeres get shorter and chromosomes get increasingly unstable. If just one of these telomeres becomes critically short, it triggers a preprogrammed pathway to cell death.
In certain cell types, this progressive shortening is countered by the enzyme telomerase, which lengthens telomeres. Such cells include the germ cells responsible for reproduction, the stem cells responsible for regeneration, and the yeast cells that are the focus of Dao Duc and Holcman’s study. This allows the possibility of a dynamic equilibrium, where the lengthening and shortening processes balance each other out (see Fig. 1, top). Dao Duc and Holcman have developed and solved a statistical mechanical model of the telomere dynamics that allows this equilibrium to be determined, thereby predicting the relationship between telomerase activity and the probability of cell death.
Statistical mechanics is increasingly used in the analysis of biological systems from gene regulation [2], to intracellular transport processes [3], to the self-propulsion of bacteria [4]. The reason for this is familiar to condensed-matter physicists: biomolecules and organisms do not exist in isolation, but interact with a complex dynamical environment. A complete description would involve tracking the interactions between trillions of molecules in a fluctuating environment. Even for the most powerful supercomputers, modeling the full mechanics of such systems is intractable. Fortunately, an accurate statistical description of a system of interest is often possible by representing the complex environment as a fluctuating force.
Dao Duc and Holcman’s starting point is the simple stochastic process that undergraduate physicists typically learn about in their first course in statistical mechanics: the random walk—a path consisting of a succession of random steps. This process is often couched in terms of a drunkard lurching from one lamppost to another in an attempt to get home after an evening of exuberance. This captures an unpredictable component of the motion; that is, that the walker is equally likely to take a step towards or away from their destination. This leads to the typical distance from the origin growing indefinitely as the square root of time, which is the defining property of diffusion. The dynamics of genetic drift, fluctuations of share prices, and the diffusion of molecules in a liquid or gas can all be modeled as a random walk.
Here, Dao Duc and Holcman use a modified random-walk model to describe the dynamics of telomere length: how the telomere grows and shrinks with each division of the cell. The model incorporates the two driving forces that determine the lengthening and shortening of telomeres. On one hand, the telomerase enzyme acts to add DNA stretches to the telomeres. On the other hand, as a cell divides via mitosis, telomeres shorten at each division because of the so-called “end replication problem”: in all higher organisms, the DNA replication machinery simply can’t copy the very ends of both DNA strands, and a little is lost in each replication event.
The authors apply their model to describe the case of yeast. Yeast cells are good proxies for germ cells and stem cells in humans—these cell types have to maintain their telomeres in order to sustain a large number of replications. (In contrast, most cells in your body lack telomerase and can only divide a finite number of times.) Experimental data for yeast suggest that while the telomere decreases by a fixed amount ( 3– 4 nucleotide base pairs) per division, the telomerase elongates the telomere by a random amount (on average 40 base pairs) with the probability of an elongation event decreasing as the telomere gets longer. Since the probabilities of shortening and lengthening are not the same and also depend on telomere length, a lengthening step may be more or less likely than a shortening step. The random walk is now “biased”: when the walker is near the origin of its walk, it is more likely to move away, whereas at large distances it is more likely to come back. In other words, short telomeres tend to get longer, while long telomeres become shorter. Our drunkard is now lurching between unevenly spaced lampposts on a steep hill.
Using such a model, the telomere length distribution reaches a steady state after a certain number of cell divisions, as illustrated in Fig 1, bottom. Dao Duc and Holcman obtain an equation for this steady-state distribution. Using this result, almost any statistical property of the telomere can be calculated accurately. These include the length’s mean and variance but also, most interestingly, the probability that the shortest telomere in a set of chromosomes falls below a critical value. In this way, this statistical mechanical model can be used to predict the probability that, after a large number of cell divisions have taken place, the next division triggers senescence and ultimately cell death.
This probability is found to depend crucially on the telomerase activity. For values characteristic of a yeast cell, Dao Duc and Holcman find that the probability of death is very small, of order 10-38. This is consistent with the fact that yeast cells undergo a large number of replications without triggering senescence [5]. The strength of this model is that, with the appropriate experimental input, it would allow properties of telomeres in other organisms to be predicted.
The importance of these results to human biology rests on the role of telomerase in both ageing and in cancer. If the activity of telomerase is increased artificially, the probability of senescence correspondingly decreases and ageing is inhibited. Unfortunately immortality comes with a price—cells that divide uncontrollably often lead to cancer. Indeed, many tumors are known to reactivate the telomerase that lies dormant in most cells in the body. This offers a narrow window of opportunity for therapeutic intervention: if we dial the telomerase activity down we can potentially suppress tumor growth; if we dial it down too far we will age before our time. Models such as Duc and Holcman’s could be an important step toward achieving this delicate balance and finding a pathway to ageing more gently.
References
- K. Dao Duc and D. Holcman, “Computing the Length of the Shortest Telomere in the Nucleus,” Phys. Rev. Lett. 111, 228104 (2013)
- K. Sneppen and G. Zocchi, Physics in Molecular Biology (Cambridge University Press, Cambridge, 2005)[Amazon][WorldCat]
- D. Chowdhury, A. Schadschneider, and K. Nishinari, “Physics of Transport and Traffic Phenomena in Biology: From Molecular Motors and Cells to Organisms,” Phys. Life Rev. 2, 318 (2005)
- M. E. Cates “Diffusive Transport without Detailed Balance in Motile Bacteria: Does Microbiology Need Statistical Physics?” Rep. Prog. Phys. 75, 042601 (2012)
- M. A Blasco, “Telomere Length, Stem Cells and Aging,” Nature Chem. Bio. 3, 640 (2007)