Winning at Quantum Dice
The ability to control individual spins (the intrinsic units of angular momentum carried by electrons) in semiconductors is an important requirement for a new generation of devices based on spin rather than charge logic. Single magnetic ions are promising for this type of application because of their long spin coherence times. The difficulty lies in addressing these stable but isolated spins, a feat that can be achieved by placing a single magnetic ion like manganese ( ) inside a semiconductor quantum dot [1]. This arrangement strongly mixes the states of the spin and the charge carriers trapped inside the nano-object. As a result, optical initialization and readout of an Mn spin state can be achieved [2] using resonant laser excitation, as employed previously in single-electron and hole spin-pumping schemes used in quantum dots [3,4]. A key feature of these established spin-pumping techniques is a depletion of the spin level that is resonantly excited, which may at first seem counterintuitive.
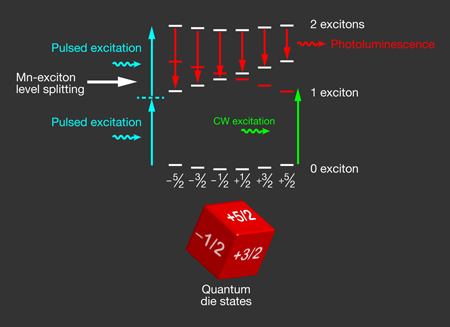
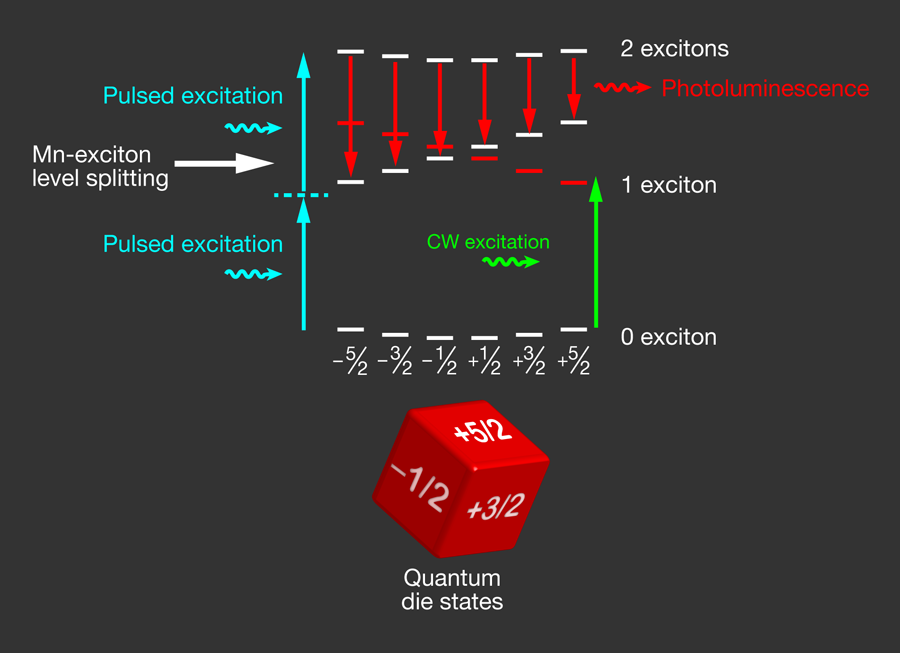
Segolene Jamet and colleagues at the French National Center for Scientific Research (CNRS) and Joseph Fourier University, France, have now experimentally demonstrated a new spin-population-trapping scheme for a single spin state [5] monitored via a new readout technique (Fig. 1). Writing in Physical Review B, they show how the atom is directly pumped into the spin state that is resonantly excited, in stark contrast to existing methods [2–4]. Tuning the laser energy and power allows varying the strength of the coherent coupling between spin levels that is at the origin of the spin-population trapping.
Researchers have demonstrated efficient optical and electrical control of individual electron and nuclear spin states in semiconductor quantum dots that allow for the integration with standard semiconductor circuits [6]. Placing an isolated ion at a fixed lattice position inside a quantum dot adds important new opportunities for spintronics because of the possibility of manipulating spins in this environment with well-established optical and electrical quantum-dot control techniques [7,8]. When a single impurity is introduced into a II-VI quantum-dot material like CdTe, as used by Jamet et al. [5], an interesting situation arises. An atom has five electrons on the shell, which results in a possible total spin of up to (in units of ). Just as a free electron can have a spin (projected on a given axis) of or , there are six different spin states for a atom from , , ,… up to . Storing information in these six spin states can be thought of as a “quantum die,” as opposed to a two-quantum-level system called “quantum bit.” Therefore the system investigated by Jamet et al. is interesting in the context of quantum computing because pairs of different quantum bits can be defined for a single impurity.
A general advantage of an isolated Mn atom in a semiconductor matrix is that these spin states can be well separated from each other in energy, even in modest magnetic fields, through what is termed the “giant Zeeman effect” [9]. Applying magnetic fields is not always feasible in real-life applications, therefore Jamet et al. lift the spin-state degeneracy through photoexcitation: The optically created electron-hole pair (exciton) strongly interacts with the electrons of the via an effect known as the Coulomb exchange interaction. As a result the quantum-dot emission, usually one single line, is split into six well-separated components. In the absence of spin pumping, such as that applied by Jamet et al., the spin state of the atom following excitation of the dot by a nonresonant laser is completely arbitrary. As a result, all six possible lines are observed in the time-averaged optical spectra [1].
Using laser excitation that is slightly off resonance with respect to the spin state (green arrow in Fig.1), Jamet et al. are able to populate mainly this targeted spin state, to which the populations from the and states have been transferred. In order for this transfer to occur, first, they needed to match the energy of the spin states. Jamet et al. arranged this through resonant excitation with a laser. The strong coupling between the electromagnetic radiation and the system shifts the states in energy as dressed states are formed [5]. Second, they needed to establish population transfer toward the state. Spin systems are, in general, very sensitive to the exact symmetry (spherical, cubic,…) of their environment. dots in a matrix are subject to lattice strain. This results in an anisotropic local environment for the electronic Mn spin system inside a strained quantum dot. As a direct consequence of the anisotropic strain distribution [10], spin states separated by two units of are coupled (i.e., coupled to not ). As the and states dressed by the laser field are brought into resonance, this coherent coupling induces a population transfer from the to the states. This population transfer is irreversible once the photon has left the dot; i.e., the optically dressed state has recombined.
The novel spin-population-trapping scheme introduced by Jamet et al. is controlled by the presence of coherent coupling between different spin states. In future experiments, this coupling can be optimized through strain engineering, i.e., using different dot-barrier material combinations with a variety of lattice parameters. Also the application of a small, external magnetic field in the dot plane will modify the coupling between spin states. The spin-population trapping for the electron also involves flips with the spin of the nucleus. Optical pumping of the spin of a single nucleus with long spin-memory times is a natural extension of the current work. In principle, the spin-population trapping introduced by Jamet et al. can be applied to other solid-state and atomic systems provided that a coherent coupling between the spin sublevels is present or can be induced.
References
- L. Besombes Y. Léger, L. Maingault, D. Ferrand, H. Mariette, and J. Cibert, “Probing the Spin State of a Single Magnetic Ion in an Individual Quantum Dot,” Phys. Rev. Lett. 93, 207403 (2004)
- C. Le Gall, R. S. Kolodka, C. L. Cao, H. Boukari, H. Mariette, J. Fernández-Rossier, and L. Besombes, “Optical Initialization, Readout, and Dynamics of a Mn Spin in a Quantum Dot,” Phys. Rev. B 81, 245315 (2010)
- M. Atatüre, J. Dreiser, A. Badolato, A. Högele, K. Karrai, and A. Imamoglu, “Quantum-Dot Spin-State Preparation with Near-Unity Fidelity,” Science 312, 551 (2006)
- B. Gerardot et al., “Optical Pumping of a Single Hole Spin in a Quantum Dot,” Nature 451, 441 (2008)
- S. Jamet, H. Boukari, and L. Besombes, “Spin dynamics of a Mn atom in a semiconductor quantum dot under resonant optical excitation,” Phys. Rev. B 87, 245306 (2013)
- Quantum Dots: Optics, Electron Transport, and Future Applications, edited by A. Tartakovskii (Cambridge University Press, Cambridge, 2012)[Amazon][WorldCat]
- E. Baudin, E. Benjamin, A. Lemaître, and O. Krebs, “Optical Pumping and a Nondestructive Readout of a Single Magnetic Impurity Spin in an InAs/GaAs Quantum Dot,” Phys. Rev. Lett. 107, 197402 (2011)
- M. Goryca, T. Kazimierczuk, M. Nawrocki, A. Golnik, J. A. Gaj, P. Kossacki, P. Wojnar, and G. Karczewski, “Optical Manipulation of a Single Mn Spin in a CdTe-Based Quantum Dot,” Phys. Rev. Lett. 103, 087401 (2009)
- J. A. Gaj, R. Planel, and G. Fishman, “Relation of Magneto-Optical Properties of Free Excitons to Spin Alignment of Mn ions in CdMnTe,” Solid State Commun. 29, 435 (1979)
- M. Qazzaz, G. Yang, S. H. Xin, L. Montes, H. Luo, and J. K. Furdyna, “Electron Paramagnetic Resonance of Mn in Strained-Layer Semiconductor Superlattices,” Solid State Commun. 96, 405 (1995)