Observing the Great Spin and Orbital Swap

Ana Maria  Rey

Viewpoint

Observing the Great Spin and Orbital Swap

JILA, NIST, and Department of Physics, University of Colorado, Boulder,CO 80309, USA

September 15, 2014• Physics 7, 95

The experimental observation of spin-orbital exchange interactions in ultracold atoms opens a window for the exploration of poorly understood magnetic behaviors.

Figure caption — **Figure 1:** Researchers place fermionic $^{173} Yb$ atoms (with nuclear spin $I = 5 / 2$ ) into a 3D optical lattice, depicted on the right. Some of the lattice sites contain two atoms, each occupying one of the two lowest electronic states (labeled $g$ and $e$ and colored orange and blue). In addition to these orbital degrees of freedom, the atoms were allowed to populate two nuclear spin degrees of freedom, $I_{z} = 5 / 2$ and $I_{z} = - 5 / 2$ , represented by $| ↑ 〉$ and $| ↓ 〉)$ , respectively. The researchers observed for the first time coherent oscillations between two spin states: $| e ↑, g ↓ 〉 \Leftrightarrow | e ↓, g ↑ 〉$ . From the oscillation frequency, they determine the spin-exchange interaction strength. This work prepares for the future use of Yb atoms as quantum simulators for spin-orbital models, which are believed to describe transition metal oxides, heavy fermion materials, and spin liquid phases.

The interplay between electronic charge, spin, and orbital degrees of freedom in solids is at the heart of the complex and exotic magnetic behavior. The electrons, whose spins play a central role in these magnetic effects, primarily interact through the Coulomb force, which is spin-independent. However, the Pauli exclusion principle imposes constraints that give rise to so-called exchange interactions, which couple the spin and orbital degrees of freedom of the electrons. The exchange coupling is not a normal force but is instead the outcome of a symmetry that a quantum system must obey when two of its electrons swap their spins and (orbital) positions. Exchange interactions are in fact the essential ingredient behind “orbital magnetism,” a phase in which electrons confined in localized orbitals interact with one another and with other valence electrons populating different orbitals. Orbital magnetism includes ferromagnetism, as well as more exotic effects like colossal magnetoresistance (an enormous decrease of resistance in certain manganese oxides exposed to an external magnetic field [1]) and heavy fermion behavior (a thousandfold increase in the effective mass of electrons in rare-earth or actinide compounds [2]). But this type of magnetism isn’t well understood: Simplified models can’t accurately describe these nontrivial magnetic behaviors and, in spite of intensive efforts, many open questions remain in our understanding of orbital magnetism and its consequences.

To shed light on the physics of orbital magnetism, researchers are looking to use fully controllable ultracold atoms as quantum simulators of spin-orbital models. These atomic systems offer unique capabilities, in that spin-orbit exchange can potentially be studied directly. Giacomo Cappellini from the European Laboratory for Non-Linear Spectroscopy in Florence, Italy, and his colleagues have taken an important step towards reaching this goal. The authors report the first direct observation of coherent spin-orbital exchange interactions using ultracold fermionic ytterbium atoms trapped in a three-dimensional optical lattice [3]. They also confirm that this system obeys a generic spin symmetry called SU( $N$ ).

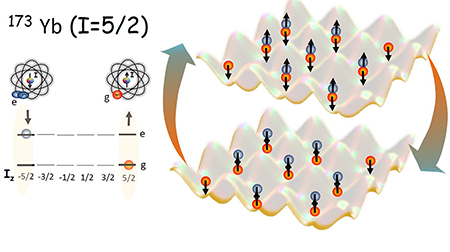
A fundamental ingredient required for simulating orbital magnetism is having atomic systems with long-lived orbital states that can be controlled without affecting the spin. Fermionic alkaline-earth atoms with two valence electrons and nonzero nuclear spin, such as strontium (Sr) or others with similar atomic structure, like ytterbium (Yb), are thought to satisfy this requirement [4]. The appeal of these atoms arises from their intrinsic atomic structure that possesses stable “clock” states consisting of a ground state, $g$ , and an extremely long-lived excited state $e$ . The excited state’s extremely long lifetime makes this type of atom ideal for timekeeping—the best atom clocks in the world now operate with $^{87} Sr$ and $^{171} Yb$ [5]. In relation to orbital magnetism, the clock states act as stable orbital degrees of freedom, decoupled from the nuclear-spin degrees of freedom. This is because the two outer electrons in the clock states do not have any net electronic angular momentum, $J = 0$ , and thus the hyperfine interactions, which generally couple electronic and nuclear spin, $I$ , degrees of freedom in atoms, vanish. The clock states and the nuclear spins, respectively, can thus be used to mimic the role of orbital and spin degrees of freedom in solid-state systems.

Besides the opportunity to simulate orbital magnetism, the electronic-nuclear-spin decoupling in alkaline-earth atoms gives rise to a novel and unique SU( $N$ ) symmetry in their collision properties, where $N$ , the number of populated nuclear spin states, can be as large as $2 I + 1$ . This symmetry means that collisions between two atoms should not depend on their nuclear spin. It is similar to how the Coulomb interaction is independent of electron spin, and indeed, one can describe electrons in solids as having SU(2) symmetry. And just as the Pauli exclusion principle imposes constraints on the spins of electrons in the same orbital, the quantum statistics imposes restrictions that, for example, forbid low-energy collisions between fermions in the same nuclear-spin state. The exchange interactions within a system obeying SU( $N$ ) symmetry can lead to frustration, a high degree of degeneracy and new types of topological phases of matter long-sought but so far not found in real materials [6].

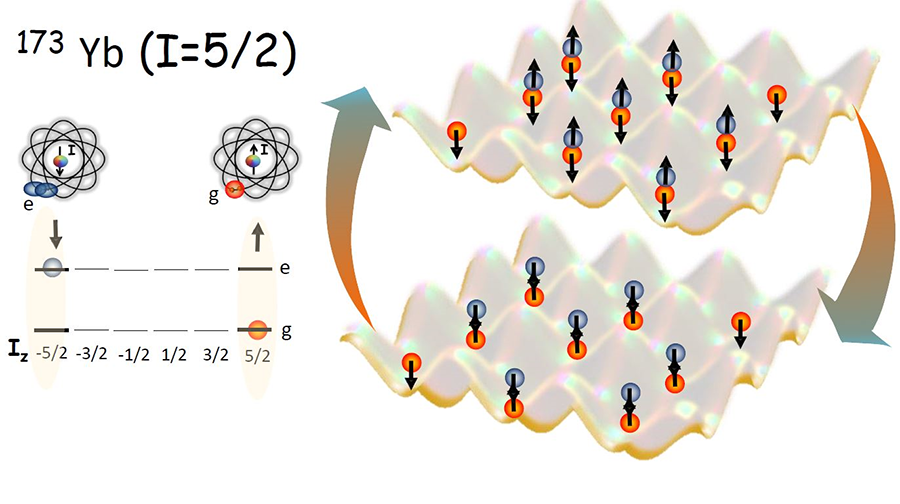
To measure the spin-orbital exchange interactions, Cappellini and collaborators loaded an array of ultracold fermionic $^{173} Yb$ atoms, with nuclear spin $I = 5 / 2$ , in a deep three-dimensional optical lattice. The lattice confinement was strong enough to freeze the motional degrees of freedom. Using lasers and a strong magnetic field, the researchers manipulated sites populated with two atoms. In particular, they prepared an initial two-atom state corresponding to a coherent superposition of the two orbitals $e$ , $g$ and two accessible spin ( $N = 2$ ) states. For the latter the nuclear-spin projections $I_{z} = 5 / 2$ and $I_{z} = - 5 / 2$ were used (see Fig.1). After letting the atoms evolve for a certain amount of time, the team measured the spin of the ground state $g$ and found that it oscillated between $I_{z} = 5 / 2$ and $I_{z} = - 5 / 2$ . The observed oscillations disappeared when atoms were prepared in the same orbital or when the swap processes were made off-resonance (i.e., in the presence of a large magnetic field) and thus could be unequivocally identified as a direct manifestation of orbital-spin exchange. From the oscillation rate, the team determined the strength of the exchange interactions. Those observations, together with additional spectroscopic measurements, allowed the researchers to determine the scattering parameters that govern the low-energy collisions between $e$ and $g$ atoms.

In a very recent work [7], researchers at the Max Planck Institute in Munich also performed similar spectroscopic measurements to determine the spin-orbital exchange interactions, however, the Florence team is the first to observe coherent oscillations that survive for long times, thus demonstrating that exchange interactions in Yb atoms can indeed dominate over other types of decoherent mechanisms. Cappellini et al. also confirmed the conservation of the nuclear-spin population during the dynamics, a smoking-gun signature of the SU $(N = 6)$ symmetry exhibited by $^{173} Yb$ . Evidence for SU( $N$ ) symmetry in alkaline-earth(like) atoms was also reported in prior experiments looking at suppressed nuclear-spin-relaxation rates and spectroscopic parameters in strontium atoms [8], reduced temperatures in a $^{173} Yb$ Mott insulator [9], and the $N$ dependence of strongly interacting one-dimensional $^{173} Yb$ atoms [10].

Although Cappellini et al. performed measurements in the limit of a deep optical lattice with pinned atoms, mainly to study two-atom collisions, their results are a clear demonstration of the dominant role of exchange interactions. They also pave the ground for the use of Yb in the simulation of magnetic models describing strongly interacting materials. For example, just by allowing tunneling between lattice sites, ultracold atoms could offer a first-principle demonstration of spin-orbital itinerant magnetism (seen in transition metals), and such simulations could access the corresponding time-resolved dynamics. Furthermore, opening the system to more than two nuclear spins could create atomic generalizations of orbital magnetic models with no direct counterpart in nature, including the fascinating, challenging, and unexplored frontier of SU( $N$ ) physics.

This research is published in Physical Review Letters.

References

Y. Tokura, Colossal Magnetoresistive Oxides (Gordon and Breach, Amsterdam, 2000)[Amazon][WorldCat]
P. Coleman, “Heavy Fermions: Electrons at the Edge of Magnetism,” in Handbook of Magnetism and Advanced Magnetic Materials, edited by H. Kronmüller and S. S. P. Parkin (John Wiley and Sons, Hoboken, 2007)[Amazon][WorldCat]
G. Cappellini et al., “Direct Observation of Coherent Interorbital Spin-Exchange Dynamics,” Phys. Rev. Lett. 113, 120402 (2014)
A. V. Gorshkov, M. Hermele, V. Gurarie, C. Xu, P. S. Julienne, J. Ye, P. Zoller, E. Demler, M. D. Lukin, and A. M. Rey, “Two-Orbital SU( $N$ ) magnetism with Ultracold Alkaline-Earth Atoms,” Nature Phys. 6, 289 (2010); C. J. Wu, J. P. Hu, and S. C. Zhang, “Exact SO(5) Symmetry in the Spin-3/2 Fermionic System,” Phys. Rev. Lett. 91, 186402 (2003); M. A. Cazalilla, A. F. Ho, and M. Ueda, “Ultracold Gases of Ytterbium: Ferromagnetism and Mott States in an SU(6) Fermi System,” New J. Phys. 11, 103033 (2009)
B. J. Bloom, T. L. Nicholson, J. R. Williams, S. L. Campbell, M. Bishof, X. Zhang, W. Zhang, S. L. Bromley, and J. Ye, “An Optical Lattice Clock with Accuracy and Stability at the $10^{- 18}$ Level,” Nature 506, 71 (2014); N. Hinkley, J. A. Sherman, N. B. Phillips, M. Schioppo, N. D. Lemke, K. Beloy, M. Pizzocaro, C.W. Oates, and A. D. Ludlow, “An Atomic Clock with $10^{- 18}$ Instability,” Science 341, 1215 (2013)
M. Hermele, V. Gurarie, and A. M. Rey, “Mott Insulators of Ultracold Fermionic Alkaline Earth Atoms: Underconstrained Magnetism and Chiral Spin Liquid,” Phys. Rev. Lett. 103, 135301 (2009)
F. Scazza, C. Hofrichter, M. Höfer, P. C. De Groot, I. Bloch, and S. Fölling, “Observation of Two-Orbital Spin-Exchange Interactions with Ultracold SU( $N$ )-Symmetric Fermions,” arXiv:1403.4761 (2014)
S. Stellmer, R. Grimm, and F. Schreck, “Detection and Manipulation of Nuclear Spin States in Fermionic Strontium,” Phys. Rev. A 84, 043611 (2011); X. Zhang, M. Bishof, S. L. Bromley, C. V. Kraus, M. S. Safronova, P. Zoller, A. M. Rey, and J. Ye, “Spectroscopic Observation of SU( $N$ )-Symmetric Interactions in Sr Orbital Magnetism,” Science 21 August 2014
S. Taie, R. Yamazaki, S. Sugawa, and Y. Takahashi, “An SU(6) Mott Insulator of an Atomic Fermi Gas Realized by Large-Spin Pomeranchuk Cooling,” Nature Phys. 8, 825 (2012)
G. Pagano et al., “A One-Dimensional Liquid of Fermions with Tunable Spin,” Nature Phys. 10, 198 (2014)

About the Author

Ana Maria Rey received her Ph.D. from the University of Maryland at College Park and NIST-Gaithersburg in 2004. She is currently a JILA fellow and a research associate professor in the physics department at the University of Colorado, Boulder. Rey’s research is on how to control and manipulate ultracold atoms, molecules, and trapped ions for use as quantum simulators of solid-state materials and for entanglement generation, quantum information, and precision measurements.

Direct Observation of Coherent Interorbital Spin-Exchange Dynamics

G. Cappellini, M. Mancini, G. Pagano, P. Lombardi, L. Livi, M. Siciliani de Cumis, P. Cancio, M. Pizzocaro, D. Calonico, F. Levi, C. Sias, J. Catani, M. Inguscio, and L. Fallani

Phys. Rev. Lett. 113, 120402 (2014)

Published September 15, 2014

Read PDF