Nuclear Spin Points out Arrow of Time
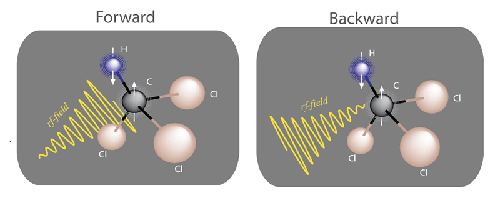
Compared to many weird-sounding concepts in physics, the idea that time has a preferred dirction seems downright obvious. After all, a broken glass won’t reassemble into one piece. But the origin of the arrow of time isn’t at all obvious to physicists. This is because the physical laws that describe microscopic systems are reversible: rewind the clock and two colliding particles will go back from where they came. Where then does irreversibility come from? Is there some undiscovered source of irreversibility at the microscopic scale? Or does it emerge when crossing some microscopic-macroscopic boundary? A new contribution to this already active dialogue [1–3] comes from Roberto Serra at the Federal University of ABC, Brazil, and colleagues [4]. They have, for the first time, experimentally measured the entropy production in a microscopic, quantum system: a nuclear spin (Fig. 1). A positive entropy production is a proxy for the arrow of time, and having measured it, the authors open the door to studying time’s arrow on the quantum scale.
What does it mean to measure time’s arrow? Formally, the existence of an arrow of time is dictated by the second law of thermodynamics, which says the entropy of a closed system can only increase [1]. And although experimentalists cannot rewind the movie of a thermodynamic transformation, they can measure by how much this rewinding is impossible. This is quantified by the entropy production, which is zero if the movie can be rewound and positive if—as is most often the case—it cannot.
This quantity, and hence time’s arrow, is what Serra and colleagues set out to measure in a quantum system. To do so, they followed a general method that involves three ingredients: an external operator, who controls a system that interacts in an uncontrolled way with a thermal bath. (The same elements are found in a heat engine, with the calorific fluid serving as the system.) A transformation corresponds to the operator using a protocol to drive the system for a period of time. For instance, the operator might change one of the system's parameters over time using an external field, and then reverse this protocol by rewinding the field's evolution.
Intuitively, entropy production will be zero if, after completion of the forward and backward protocols, the system returns to its starting point. This can occur in at least two situations. The first is a system isolated from any bath and fully controlled by the operator. This “trivial” case shows the critical role of the bath in the emergence of the arrow of time: the bath randomizes the dynamics and without it, processes are reversible. But there is a second case in which a transformation is reversible in the presence of a bath. For this to happen, the system must be driven sufficiently slowly that, at any time in the protocol, the system is allowed to reach equilibrium with the bath. This type of adiabatic process corresponds to the most efficient way of operating heat engines, such as the celebrated Carnot engine [5].
A transformation can, however, be performed so fast that the system is driven out of equilibrium. This leads to a positive entropy production and a definite arrow of time. Departure from equilibrium can happen if the system is driven faster than the time it needs to relax to equilibrium with the bath (classical adiabicity breaking) or if it is driven faster than its typical transition frequency (quantum adiabicity breaking). It is the latter regime that Serra and colleagues have experimentally investigated.
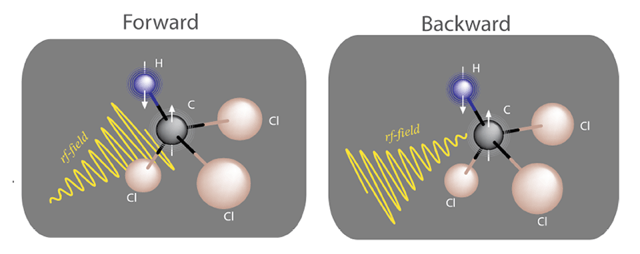
To do so, they utilized nuclear magnetic resonance (NMR), which is one of the best experimental methods to date for studying thermodynamics on the quantum scale. The system they studied is an ensemble of spin-1/2 particles, where each spin is from a carbon-13 nucleus in a chloroform molecule in a liquid. One measurement on this ensemble corresponds to repeating a measurement many times on a single spin. The external field of their forward protocol is a time-varying magnetic field pulse; the backward protocol is simply this same pulse flipped in time (Fig. 2). They imposed thermal equilibrium before running each protocol by applying carefully chosen sequences of magnetic pulses. Because of this thermalizing step, work done on the spin or by the spin is stochastic (random). And it is quantized because of the spin’s quantum nature.
They measured entropy production in two independent ways. First, they used NMR tomography to determine the distribution of quantum states occupied by the carbon-13 spins before and after applying the forward and reverse protocols. The relative entropy between these two distributions quantifies how different they are and exactly corresponds to the mean entropy production. Second, they used an interferometric technique [6] to detect changes in the spins’ energy distribution during the forward protocol and during the backward protocol. These changing distributions correspond to the (quantum) probability of work being done on or by the system. The log of the ratio of these two probabilities is, according to a theoretical relation [7], equal to the entropy production. In this way, the authors were able to extract the average entropy production and compare it to the directly measured value, finding very good agreement. Such a comparison provides a check on the idea that entropy production is a physical quantity and not just a theoretical definition.
Serra and colleagues have demonstrated that it is possible to perform controlled thermodynamic experiments in the quantum regime. This ability opens the door to a better understanding of the origin and consequences of the arrow of time. It will, for example, allow researchers to explore fundamental questions in the areas of quantum information and thermodynamics. In particular, how does irreversibility relate to the loss of quantum information or quantum coherence [8]? Could quantum thermodynamics lead to new criteria with which to distinguish different interpretations of quantum mechanics? How is irreversibility quantitatively related to the energetic cost of quantum computation [9]? The exciting conversation between thermodynamics and quantum physics continues.
This research is published in Physical Review Letters.
References
- A. S. Eddington, The Nature of the Physical World (Cambridge University Press, Cambridge, 1928)[Amazon][WorldCat].
- C. Jarzynski, “Equalities and Inequalities: Irreversibility and the Second Law of Thermodynamics at the Nanoscale,” Annu. Rev. Condens. Matter Phys. 2, 329 (2011).
- J. L. Lebowitz, “Boltzmann's Entropy and Time's Arrow,” Phys. Today 46, No. 9, 32 (1993).
- T. B. Batalhão, A. M. Souza, R. S. Sarthour, I. S. Oliveira, M. Paternostro, E. Lutz, and R. M. Serra, “Irreversibility and the Arrow of Time in a Quenched Quantum System,” Phys. Rev. Lett. 115, 190601 (2015).
- S. Carnot, Réflexion sur la puissance motrice du feu (Bachelier, Paris, 1824)[Amazon][WorldCat].
- T. B. Batalhão, A. M. Souza, L. Mazzola, R. Auccaise, R. S. Sarthour, I. S. Oliveira, J. Goold, G. De Chiara, M. Paternostro, and R. M. Serra, “Experimental Reconstruction of Work Distribution and Study of Fluctuation Relations in a Closed Quantum System,” Phys. Rev. Lett. 113, 140601 (2014).
- G. E. Crooks, “Entropy Production Fluctuation Theorem and the Nonequilibrium Work Relation for Free Energy Differences,” Phys. Rev. E 60, 2721 (1999).
- W. H. Zurek, “Decoherence, Einselection, and the Quantum Origins of the Classical,” Rev. Mod. Phys. 75, 715 (2003).
- V. Vedral, “The Role of Relative Entropy in Quantum Information Theory,” Rev. Mod. Phys. 74, 197 (2002).