Viewpoint

Closing the Door on Einstein and Bohr’s Quantum Debate

    Alain Aspect
    • Laboratoire Charles Fabry, Institut d'Optique Graduate School, CNRS, Université Paris-Saclay, Palaiseau, France
• Physics 8, 123
By closing two loopholes at once, three experimental tests of Bell’s inequalities remove the last doubts that we should renounce local realism. They also open the door to new quantum information technologies.
APS/Alan Stonebraker
Figure 1: An apparatus for performing a Bell test. A source emits a pair of entangled photons 𝜈1 and 𝜈2. Their polarizations are analyzed by polarizers A and B (grey blocks), which are aligned, respectively, along directions a and b. (a and b can be along x, y or any direction in the x-y plane; here, they are along x.) Each polarizer has two output channels, labeled +1 and -1. A photon 𝜈1 polarized parallel (perpendicular) to a will emerge in +1 (-1) at A. Similarly, a photon 𝜈2 polarized parallel (perpendicular) to b will emerge in +1 (-1) at B. But in general, the photons are not in a state of polarization corresponding to a specific output channel, and then the formalism of quantum mechanics yields the probabilities of getting results +1 or -1, for specified orientations of the polarizers. For the entangled state of two polarized photons (Ψ) shown here, the quantum formalism predicts random results on each side (a 50% probability of being +1 or -1.) But it also predicts strong correlations between these random results. For instance, if both polarizers are aligned along the same direction (a=b), then the results at A and B will be either (+1,+1) or (-1,-1), but never (+1,-1) or (-1,+1): this is a total correlation, as can be determined by measuring the four rates with the fourfold detection circuit (green). Local realism explains these correlations by assuming a common property of the two photons, whose value changes randomly from one photon pair to the next. Bell’s inequality, however, shows the correlations predicted by local realism are limited; but quantum predictions violate this inequality. A Bell test consists of measuring the correlations and comparing the results with Bell’s inequalities. To perform an “ideal” Bell test, the polarizer settings must be changed randomly while the photons are in flight between the source and the polarizers, and the detector efficiencies should exceed 2/3 (see text for details).

In 1935, Albert Einstein, Boris Podolsky, and Nathan Rosen (EPR) wrote a now famous paper questioning the completeness of the formalism of quantum mechanics. Rejecting the idea that a measurement on one particle in an entangled pair could affect the state of the other—distant—particle, they concluded that one must complete the quantum formalism in order to get a reasonable, “local realist,” description of the world. This view says a particle carries with it, locally, all the properties determining the results of any measurement performed on it. (The ensemble of these properties constitutes the particle’s physical reality.) It wasn’t, however, until 1964 that John Stewart Bell, a theorist at CERN, discovered inequalities that allow an experimental test of the predictions of local realism against those of standard quantum physics. In the ensuing decades, experimentalists performed increasingly sophisticated tests of Bell’s inequalities. But these tests have always had at least one “loophole,” allowing a local realist interpretation of the experimental results unless one made a supplementary (albeit reasonable) hypothesis. Now, by closing the two main loopholes at the same time, three teams have independently confirmed that we must definitely renounce local realism [1–3]. Although their findings are, in some sense, no surprise, they crown decades of experimental effort. The results also place several fundamental quantum information schemes, such as device-independent quantum cryptography and quantum networks, on firmer ground.

It is sometimes forgotten that Einstein played a major role in the early development of quantum physics [4]. He was the first to fully understand the consequences of the energy quantization of mechanical oscillators, and, after introducing “lichtquanten‚” in his famous 1905 paper, he enunciated as early as 1909 the dual wave-particle nature of light [5]. Despite his visionary understanding, he grew dissatisfied with the “Copenhagen interpretation” of the quantum theory, developed by Niels Bohr, and tried to find an inconsistency in the Heisenberg uncertainty relations. At the Solvay conference of 1927, however, Bohr successfully refuted all of Einstein’s attacks, making use of ingenious gedankenexperiments bearing on a single quantum particle.

But in 1935, Einstein raised a new objection about the Copenhagen interpretation, this time with a gedankenexperiment involving two particles. He had discovered that the quantum formalism allows two particles to be entangled in a state such that strong correlations are predicted between measurements on these two particles. These correlations would persist at particle separations large enough that the measurements could not be directly connected by any influence, unless it were to travel faster than light. Einstein therefore argued for what he felt was the only reasonable description: that each particle in the pair carries a property, decided at the moment of separation, which determines the measurement results. But since entangled particles are not described separately in the quantum formalism, Einstein concluded the formalism was incomplete [6]. Bohr, however, strongly opposed this conclusion, convinced that it was impossible to complete the quantum formalism without destroying its self-consistency [7].

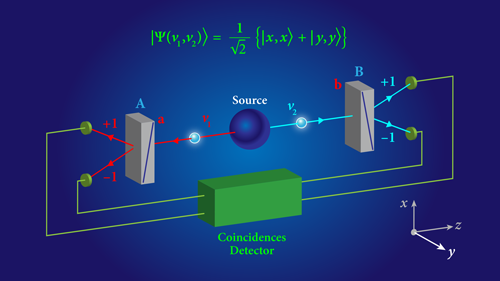
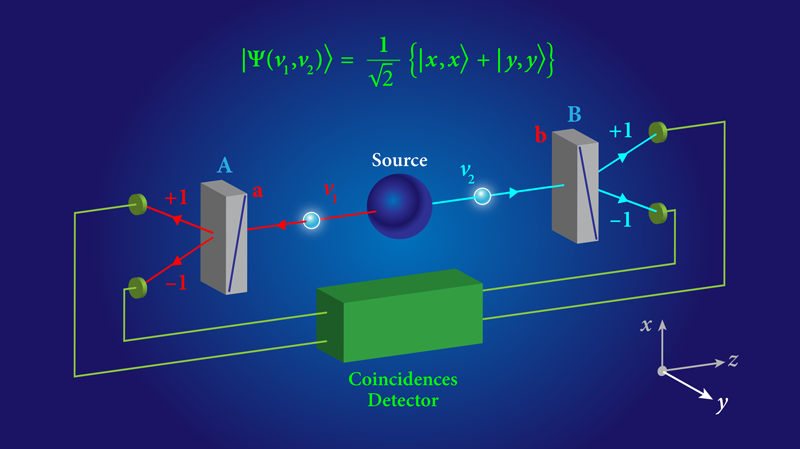
With the exception of Erwin Schrödinger [8], most physicists did not pay attention to the debate between Bohr and Einstein, as the conflicting views only affected one’s interpretation of the quantum formalism and not its ability to correctly predict the results of measurements, which Einstein did not question. The situation changed when Bell made the groundbreaking discovery that some predictions of quantum physics conflict with Einstein’s local realist world view [9, 10]. To explain Bell’s finding, it helps to refer to an actual experiment, consisting of a pair of photons whose polarizations are measured at two separate stations (Fig. 1). For the entangled state (Ψ) of two polarized photons shown in the inset, quantum mechanics predicts that the polarization measurements performed at the two distant stations will be strongly correlated. To account for these correlations, Bell developed a general local realist formalism, in which a common property, attributed to each photon of a pair, determines the outcomes of the measurements. In what are now known as Bell’s inequalities, he showed that, for any local realist formalism, there exist limits on the predicted correlations. And he showed that, according to quantum mechanics, these limits are passed for some polarizer settings. That is, quantum-mechanical predictions conflict with local realism, in contradiction with the belief that the conflict was only about interpretation, not about quantitative predictions.

Bell’s discovery thus shifted Einstein and Bohr’s debate from epistemology to the realm of experimental physics. Within a few years, Bell’s inequalities were adapted to a practical scheme [11]. The first experiments were carried out in 1972 at the University of California, Berkeley [12], and at Harvard [13], then in 1976 at Texas A&M [14]. After some initial discrepancies, the results converged towards an agreement with quantum mechanics and a violation of Bell’s inequalities by as much as 6 standard deviations. But although these experiments represented genuine tours de force for the time, they were far from ideal. Some loopholes remained open, allowing a determined advocate of Einstein’s point of view to interpret these experiments in a local realist formalism [15].

The first—and according to Bell [16], the most fundamental—of these loopholes is the “locality loophole.” In demonstrating his inequalities, Bell had to assume that the result of a measurement at one polarizer does not depend on the orientation of the other. This locality condition is a reasonable hypothesis. But in a debate where one envisages new phenomena, it would be better to base such a condition on a fundamental law of nature. In fact, Bell proposed a way to do this. He remarked that if the orientation of each polarizer was chosen while the photons were in flight, then relativistic causality—stating that no influence can travel faster than light—would prevent one polarizer from “knowing” the orientation of the other at the time of a measurement, thus closing the locality loophole [9].

This is precisely what my colleagues and I did in 1982 at Institut d'Optique, in an experiment in which the polarizer orientations were changed rapidly while the photons were in flight [17] (see note in Ref. [18]). Even with this drastically new experimental scheme, we found results still agreeing with quantum predictions, violating Bell’s inequality by 6 standard deviations. Because of technical limitations, however, the choice of the polarizer orientations in our experiment was not fully random. In 1998, researchers at the University of Innsbruck, using much improved sources of entangled photons [19] were able to perform an experiment with genuine random number generators, and they observed a violation of Bell’s inequality by several tens of standard deviations [20].

There was, however, a second loophole. This one relates to the fact that the detected pairs in all these experiments were only a small fraction of the emitted pairs. This fraction could depend on the polarizer settings, precluding a derivation of Bell’s inequalities unless one made a reasonable “fair sampling” hypothesis [21]. To close this “detection loophole,” and drop the necessity of the fair sampling hypothesis, the probability of detecting one photon when its partner has been detected (the global quantum efficiency, or “heralding” efficiency) must exceed 2/3—a value not attainable for single-photon counting technology until recently. In 2013, taking advantage of new types of photodetectors with intrinsic quantum efficiencies over 90%, two experiments closed the detection loophole and found a clear violation of Bell’s inequalities [22, 23]. The detection loophole was also addressed with other systems, in particular using ions instead of photons [24, 25], but none of them tackled simultaneously the locality loophole.

So as of two years ago, both the locality loophole and the detection loopholes had been closed, but separately. Closing the two loopholes together in one experiment is the amazing achievement by the research teams led by Ronald Hanson at Delft University of Technology in the Netherlands [1], Anton Zeilinger at the University of Vienna, Austria [2], and Lynden Shalm at NIST in Boulder, Colorado [3].

The experiments by the Vienna [2] and NIST [3] groups are based on the scheme in Fig. 1. The teams use rapidly switchable polarizers that are located far enough from the source to close the locality loophole: The distance is 30 meters in the Vienna experiment and more than 100 meters in the Boulder experiment. Both groups also use high-efficiency photon detectors, as demanded to close the detection loophole. They prepare pairs of photons using a nonlinear crystal to convert a pump photon into two “daughter” entangled photons. Each photon is sent to a detection station with a polarizer whose alignment is set using a new type of random number generator developed by scientists in Spain [26] (see 16 December 2015 Synopsis; the same device was used by the Delft group). Moreover, the two teams achieved an unprecedentedly high probability that, when a photon enters one analyzer, its partner enters the opposite analyzer. This, combined with the high intrinsic efficiency of the detectors, gives both experiments a heralding efficiency of about 75%—a value larger than the critical value of 2/3.

The authors evaluate the confidence level of their measured violation of Bell’s inequality by calculating the probability p that a statistical fluctuation in a local realist model would yield the observed violation. The Vienna team reports a p of 3.7×10−31—a spectacular value corresponding to a violation by more than 11 standard deviations. (Such a small probability is not really significant, and the probability that some unknown error exists is certainly larger, as the authors rightly emphasize.) The NIST team reports an equally convincing p of 2.3×10−7, corresponding to a violation by 7 standard deviations.

The Delft group uses a different scheme [1]. Inspired by the experiment of Ref. [25], their entanglement scheme consists of two nitrogen vacancy (NV) centers, each located in a different lab. (An NV center is a kind of artificial atom embedded in a diamond crystal.) In each NV center, an electron spin is associated with an emitted photon, which is sent to a common detection station located between the labs housing the NV centers. Mixing the two photons on a beam splitter and detecting them in coincidence entangles the electron spins on the remote NV centers. In cases when the coincidence signal is detected, the researchers then keep the measurements of the correlations between the spin components and compare the resulting correlations to Bell’s inequalities. This is Bell’s “event-ready” scheme [16], which permits the detection loophole to be closed because for each entangling signal there is a result for the two spin-component measurements. The impressive distance between the two labs (1.3 kilometers) allows the measurement directions of the spin components to be chosen independently of the entangling event, thus closing the locality loophole. The events are extremely rare: The Delft team reports a total of 245 events, which allows them to obtain a violation of Bell’s inequality with a p of 4×10−2, corresponding to a violation by 2 standard deviations.

The schemes demonstrated by the Vienna, NIST, and Delft groups have important consequences for quantum information. For instance, a loophole-free Bell’s inequality test is needed to guarantee the security of some device-independent quantum cryptography schemes [27]. Moreover, the experiment by the Delft group, in particular, shows it is possible to entangle static quantum bits, offering a basis for long distance quantum networks [28, 29].

Of course we must remember that these experiments were primarily meant to settle the conflict between Einstein’s and Bohr’s points of view. Can we say that the debate over local realism is resolved? There is no doubt that these are the most ideal experimental tests of Bell’s inequalities to date. Yet no experiment, as ideal as it is, can be said to be totally loophole-free. In the experiments with entangled photons, for example, one could imagine that the photons’ properties are determined in the crystal before their emission, in contradiction with the reasonable hypothesis explained in the note in Ref. [18]. The random number generators could then be influenced by the properties of the photons, without violating relativistic causality. Far fetched as it is, this residual loophole cannot be ignored, but there are proposals for how to address it [30].

Yet more foreign to the usual way of reasoning in physics is the “free-will loophole.” This is based on the idea that the choices of orientations we consider independent (because of relativistic causality) could in fact be correlated by an event in their common past. Since all events have a common past if we go back far enough in time—possibly to the big bang—any observed correlation could be justified by invoking such an explanation. Taken to its logical extreme, however, this argument implies that humans do not have free will, since two experimentalists, even separated by a great distance, could not be said to have independently chosen the settings of their measuring apparatuses. Upon being accused of metaphysics for his fundamental assumption that experimentalists have the liberty to freely choose their polarizer settings, Bell replied [31]: “Disgrace indeed, to be caught in a metaphysical position! But it seems to me that in this matter I am just pursuing my profession of theoretical physics.” I would like to humbly join Bell and claim that, in rejecting such an ad hoc explanation that might be invoked for any observed correlation, “I am just pursuing my profession of experimental physics.”

This research is published in Physical Review Letters and Nature.

References

  1. B. Hensen et al., “Loophole-free Bell Inequality Violation Using Electron Spins Separated by 1.3 Kilometres,” Nature 526, 682 (2015).
  2. M. Giustina et al., “Significant-Loophole-Free Test of Bell's Theorem with Entangled Photons,” Phys. Rev. Lett. 115, 250401 (2015).
  3. L. K. Shalm et al., “Strong Loophole-Free Test of Local Realism,” Phys. Rev. Lett. 115, 250402 (2015).
  4. A. D. Stone, Einstein and the Quantum (Princeton University Press, 2013)[Amazon][WorldCat].
  5. A. Einstein, “On the evolution of our vision on the nature and constitution of radiation,” Physikalische Zeitschrift 10, 817 (1909), English translation available at http://einsteinpapers.press.princeton.edu/vol2-trans/393.
  6. A. Einstein, B. Podolsky, and N. Rosen, “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?,” Phys. Rev. 47, 777 (1935).
  7. N. Bohr, “Can Quantum-Mechanical Description of Physical Reality be Considered Complete?,” Phys. Rev. 48, 696 (1935).
  8. E. Schrödinger and M. Born, “Discussion of Probability Relations between Separated Systems,” Math. Proc. Camb. Phil. Soc. 31, 555 (1935).
  9. J. S. Bell, “On the Einstein-Podolsky-Rosen Paradox,” Physics 1, 195 (1964), this hard to find paper is reproduced in Ref. [10].
  10. J. S. Bell, “Speakable and Unspeakable in Quantum Mechanics,” (Cambridge University Press, Cambridge, 2004)[Amazon][WorldCat].
  11. J. F. Clauser, M. A. Horne, A. Shimony, and R. A. Holt, “Proposed Experiment to Test Local Hidden-Variable Theories,” Phys. Rev. Lett. 23, 880 (1969).
  12. S. J. Freedman and J. F. Clauser, “Experimental Test of Local Hidden-Variable Theories,” Phys. Rev. Lett. 28, 938 (1972).
  13. R. A. Holt, Ph.D. thesis, Harvard (1973); F. M. Pipkin, “Atomic Physics Tests of the Basic Concepts in Quantum Mechanics,” Adv. At. Mol. Phys. 14, 281 (1979); The violation of Bell's inequality reported in this work is contradicted by J. F. Clauser, “Experimental Investigation of a Polarization Correlation Anomaly,” Phys. Rev. Lett. 36, 1223 (1976).
  14. E. S. Fry and R. C. Thompson, “Experimental Test of Local Hidden-Variable Theories,” Phys. Rev. Lett. 37, 465 (1976).
  15. J. F. Clauser and A. Shimony, “Bell's Theorem. Experimental Tests and Implications,” Rep. Prog. Phys. 41, 1881 (1978).
  16. J. S. Bell, “Atomic-Cascade Photons and Quantum Mechanical Non-Locality,” Comments At. Mol. Phys. 9, 121 (1980), reproduced in Ref. [10].
  17. A. Aspect, J. Dalibard, and G. Roger, “Experimental Test of Bell's Inequalities Using Time- Varying Analyzers,” Phys. Rev. Lett. 49, 1804 (1982).
  18. Note that rapidly switching the polarizers also closes the “freedom of choice” loophole—the possibility that the choice of the polarizer settings and the properties of the photons are not independent—provided that the properties of each photon pair are determined at its emission, or just before.
  19. A. Aspect, “Bell's Inequality Test: More Ideal Than Ever,” Nature 398, 189 (1999), this paper reviews Bell's inequalities tests until 1998, including long distance tests permitted by the development of much improved sources of entangled photons..
  20. G. Weihs, T. Jennewein, C. Simon, H. Weinfurter, and A. Zeilinger, “Violation of Bell's Inequality under Strict Einstein Locality Conditions,” Phys. Rev. Lett. 81, 5039 (1998).
  21. Prior to the availability of high-quantum efficiency detection, the violation of Bell's inequality was significant only with the “fair sampling assumption,” which says the detectors select a non-biased sample of photons, representative of the whole ensemble of pairs. In 1982, with colleagues, we found a spectacular violation of Bell’s inequalities (by more than 40 standard deviations) in an experiment in which we could check that the size of the selected sample was constant. Although this observation was consistent with the fair sampling hypothesis, it was not sufficient to fully close the detection loophole. See A. Aspect, P. Grangier, and G. Roger, “Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell's Inequalities,” Phys. Rev. Lett. 49, 91 (1982).
  22. M. Giustina et al., “Bell Violation Using Entangled Photons without the Fair-Sampling Assumption,” Nature 497, 227 (2013).
  23. B. G. Christensen et al., “Detection-Loophole-Free Test of Quantum Nonlocality, and Applications,” Phys. Rev. Lett. 111, 130406 (2013).
  24. M. A. Rowe, D. Kielpinski, V. Meyer, C. A. Sackett, W. M. Itano, C. Monroe, and D. J. Wineland, “Experimental Violation of a Bell’s Inequality with Efficient Detection,” Nature 409, 791 (2001).
  25. D. N. Matsukevich, P. Maunz, D. L. Moehring, S. Olmschenk, and C. Monroe, “Bell Inequality Violation with Two Remote Atomic Qubits,” Phys. Rev. Lett. 100, 150404 (2008).
  26. C. Abellán et al., “Generation of Fresh and Pure Random Numbers for Loophole Free Bell Tests,” Phys. Rev. Lett. 115, 250403 (2015).
  27. A. Acín, N. Brunner, N. Gisin, S. Massar, S. Pironio, and V. Scarani, “Device-Independent Security of Quantum Cryptography against Collective Attacks,” Phys. Rev. Lett. 98, 230501 (2007).
  28. L.-M. Duan, M. D. Lukin, J. I. Cirac, and P. Zoller, “Long-Distance Quantum Communication with Atomic Ensembles and Linear Optics,” Nature 414, 413 (2001).
  29. H. J. Kimble, “The Quantum Internet,” Nature 453, 1023 (2008).
  30. Should experimentalists decide they want to close this far-fetched loophole, they could base the polarizers’ orientations on cosmologic radiation received from opposite parts of the Universe. J. Gallicchio, A. S. Friedman, and D. I. Kaiser, “Testing Bell’s Inequality with Cosmic Photons: Closing the Setting-Independence Loophole,” Phys. Rev. Lett. 112, 110405 (2014).
  31. J. S. Bell, “Free Variables and Local Causality,” Epistemological Letters, February 1977, (1977), reproduced in Ref. [10].

About the Author

Image of Alain Aspect

Alain Aspect is an alumnus of the École Normal Supériere (ENS) in Cachan and the Université d'Orsay. He has held positions at the Institut d'Optique, the ENS in Yaoundé (Cameroon), ENS in Cachan, ENS/Collège de France, and CNRS. He is currently a professor both at the Institut d'Optique Graduate School, where he holds the Augustin Fresnel chair, and at École Polytechnique, in Palaiseau. He is a member of science academies in France, the USA, Austria, Belgium, and the UK. He is the recipient of the CNRS Gold medal, the Wolf Prize in Physics, the Balzan prize on quantum information, the Niels Bohr Gold medal, the Albert Einstein medal, the Ives medal of the OSA and other awards. His research has focused on tests of Bell's inequalities with entangled photons, wave-particle duality for single photons, laser cooling of atoms with lasers below the one-photon recoil, quantum simulation, and quantum atom optics with ultracold atoms (More details on: http://www.lcf.institutoptique.fr/Alain-Aspect-homepage). Photo credit: Jean-François Dars.

Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons

Marissa Giustina, Marijn A. M. Versteegh, Sören Wengerowsky, Johannes Handsteiner, Armin Hochrainer, Kevin Phelan, Fabian Steinlechner, Johannes Kofler, Jan-Åke Larsson, Carlos Abellán, Waldimar Amaya, Valerio Pruneri, Morgan W. Mitchell, Jörn Beyer, Thomas Gerrits, Adriana E. Lita, Lynden K. Shalm, Sae Woo Nam, Thomas Scheidl, Rupert Ursin, Bernhard Wittmann, and Anton Zeilinger

Phys. Rev. Lett. 115, 250401 (2015)

Published December 16, 2015

Read PDF

Strong Loophole-Free Test of Local Realism

Lynden K. Shalm et al.

Phys. Rev. Lett. 115, 250402 (2015)

Published December 16, 2015

Read PDF

Subject Areas

Quantum InformationOpticsQuantum Physics

Related Articles

Chiral Response of Achiral Meta-Atoms
Condensed Matter Physics

Chiral Response of Achiral Meta-Atoms

Contrary to conventional wisdom, a lattice of engineered nanoparticles called meta-atoms can have a chiral optical response even when each meta-atom is not chiral. Read More »

Delay Detected in Photon Generation
Optics

Delay Detected in Photon Generation

The observation of a previously unseen photon delay in the production of quantum light has implications for the development of quantum technologies. Read More »

Quantifying the Background Radiation Hitting Superconducting Qubits
Quantum Physics

Quantifying the Background Radiation Hitting Superconducting Qubits

Researchers have characterized the naturally occurring background radiation hitting a typical quantum circuit—a result that might help with the engineering of devices that are less vulnerable to radiation-induced decoherence. Read More »

More Articles