A More Precise Higgs Boson Mass

Chris Quigg

Viewpoint

A More Precise Higgs Boson Mass

Fermi National Accelerator Laboratory, P.O. Box 500, Batavia, IL 60510, USA
Institut de Physique Théorique Philippe Meyer, École Normale Supérieure, Paris, France

May 14, 2015• Physics 8, 45

A new value for the Higgs boson mass will allow stronger tests of the standard model and of theories about the Universe’s stability.

Figure caption — **Figure 1:** Values of the top quark and $W$ boson masses measured in experiments (green) and inferred from calculations (blue). The inner and outer ellipses represent 68% and 95% confidence levels, respectively, for the measured and inferred values. Within current experimental and theoretical uncertainties, the two ways of determining the top quark and $W$ boson masses agree. A more precise value of the Higgs mass would narrow the width of the blue ellipses, whereas improved measurements of the top quark and $W$ boson masses would shrink the green ellipses, making for a more incisive test for new physics. (Note, the calculations assume the Higgs mass has a central value of $125.14 GeV$ , which differs insignificantly from the new measurement by ATLAS and CMS, but does not affect the width of the blue ellipses.)

A great insight of twentieth-century science is that symmetries expressed in the laws of nature need not be manifest in the outcomes of those laws. Consider the snowflake. Its structure is a consequence of electromagnetic interactions, which are identical from any direction, but a snowflake only looks the same when rotated by multiples of $60^{\circ}$ about a single axis. The full symmetry is hidden by the particular conditions under which the water molecules crystallize. Similarly, a symmetry relates the electromagnetic and weak interactions in the standard model of particle physics, but we know it must be concealed because the weak interactions appear much weaker than electromagnetism. To learn what distinguishes electromagnetism from the weak interactions was an early goal of experiments at CERN’s Large Hadron Collider (LHC). A big part of the answer was given in mid-2012, when the ATLAS and CMS Collaborations at the LHC announced the discovery of the Higgs boson in the study of proton–proton collisions [1]. Now the discovery teams have pooled their data analyses to produce a measurement of the Higgs boson mass with $0.2 %$ precision [2]. The new value enables physicists to make more stringent tests of the electroweak theory and of the Higgs boson’s properties.

The electroweak theory [3] is a key element of the standard model of particle physics that weaves together ideas and observations from diverse areas of physics [4]. In the theory, interactions are prescribed by gauge symmetries. If nature displayed these symmetries explicitly, the force particles would all be massless, whereas we know experimentally that the weak interactions must—because they are short-ranged—be mediated by massive particles. The so-called Higgs field was introduced to the electroweak theory to hide the gauge symmetry, leading to weak force particles ( $W^{\pm}$ and $Z^{0}$ ) that have mass but a photon that is massless.

The Higgs boson is a spin-zero excitation of the Higgs field and the “footprint” of the mechanism that hides the electroweak gauge symmetry in the standard model. The Higgs boson’s interactions are fully specified in terms of known couplings and masses of its decay products, but the theory does not predict its mass. Instead, experimentalists must measure the energies and momenta of the Higgs boson’s decay products and determine its mass using kinematical equations. Once that mass is known, the rates at which the Higgs boson decays into different particles can be predicted with high precision, and compared with experiment. For a mass in the neighborhood of $125$ giga-electron-volts ( $GeV$ ), the electroweak theory foresees a happy circumstance in which several decay paths occur at large enough rates to be detected.

ATLAS and CMS are large, broad-acceptance detectors located in multistory caverns about $100$ meters below ground [5]. In the discovery run of the LHC, the ATLAS and CMS Collaborations searched for decays of a Higgs boson into bottom-quark–antiquark pairs, tau-lepton pairs, and pairs of electroweak gauge bosons: two photons, $W^{+} W^{-}$ , and $Z^{0} Z^{0}$ . The actual discovery was based primarily on mass peaks associated with either the two-photon final states or $Z^{0} Z^{0}$ pairs decaying to four-lepton (electrons or muons) final states. These channels, for which the ATLAS and CMS detectors have the best mass resolution, form the basis of their new report.

Both of the “high-resolution” final states are relatively rare: the standard model predicts that only about $1 / 4 %$ of Higgs boson decays produce two-photon states; the four-lepton rate is predicted to be nearly 20 times smaller. The two-photon channel exhibits a narrow resonance peak that contains several hundred events per experiment; the $Z^{0} Z^{0}$ to four-lepton channel yields only a few tens of signal events per experiment. To see these events in the first run of the LHC, the ATLAS and CMS collaborations chose different detector technologies, and therefore different measurement and calibration methods [2]. These differences make pooling the data complicated, but also allow the experimentalists to cross-check systematic uncertainties in their separate measurements. Their combined analyses yield a Higgs boson mass of $125.09 \pm 0.24 GeV$ , the precision of which is limited by statistics and by uncertainties in the energy or momentum scale of the ATLAS and CMS detectors.

The first consequence of the new, precise mass value is sharper predictions, within the standard model, for the relative probabilities of different Higgs boson decay modes and production rates [6]. So far, the measured decay modes and production rates agree with standard-model predictions. The current uncertainties in the measured rates are large, but they will be narrowed in the coming runs at the LHC and at possible future colliders. Evidence of any deviation would suggest that the Higgs boson does not follow the standard model textbook, or that new particles or new forces are implicated in its decays.

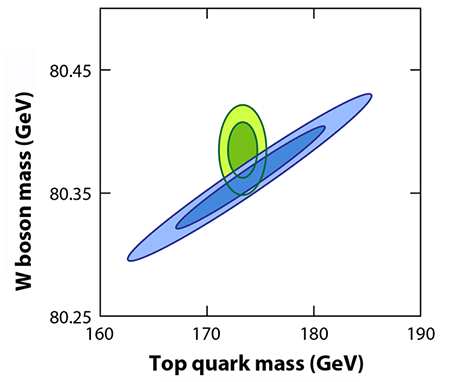
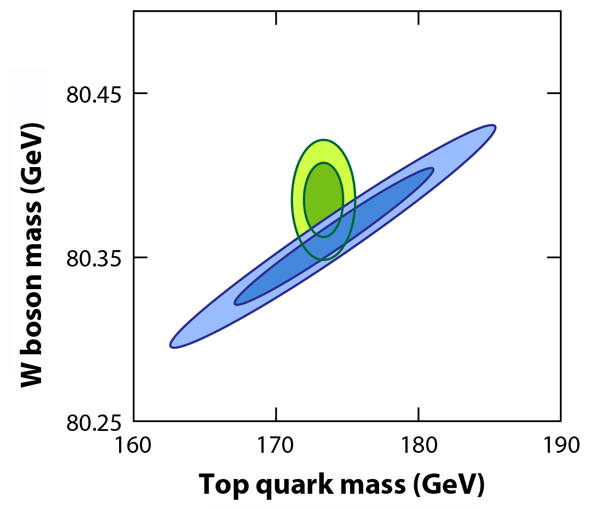
With a precisely known Higgs boson mass $M_{H}$ , theorists can also make more refined predictions of the quantum corrections to many observables, such as the $Z^{0}$ decay rates. These predictions test the consistency of the electroweak theory as a quantum field theory. Figure 1 illustrates a telling example [7]. The diagonal blue ellipses show the values of the $W$ boson and top quark masses required to reproduce a selection of electroweak observables once $M_{H}$ is fixed. (The narrow and wide ellipses represent $68 %$ and $95 %$ confidence levels, respectively.) The range of masses depends on $M_{H}$ , and the precision with which it is known controls the width of the blue ellipses. The preferred range overlaps the green ellipses, which show the directly measured values of the $W$ boson and top quark masses. In the future, more precise values for the masses of the Higgs boson, $W$ boson, and top quark could unveil a discrepancy that might lead to the discovery of new physics.

The specific value of $M_{H}$ constrains speculations about physics beyond the standard model, including supersymmetric or composite models. Perhaps most provocative of all is the possibility that the measured value of the mass is special. Quantum corrections influence not just the predictions for observable quantities, but also the shape of the Higgs potential that lies behind electroweak symmetry breaking in the standard model. According to recent analyses, the newly reported value of the Higgs boson mass corresponds to a near-critical situation in which the Higgs vacuum does not lie at the state of lowest energy, but in a metastable state close to a phase transition [8]. This might imply that our Universe is living on borrowed time, or that the electroweak theory must be augmented in some way.

With LHC Run 2 about to commence, now at higher energies, particle physicists can look forward to a new round of exploration, searches for new phenomena, and refined measurements. Combined analyses and critical evaluations, such as the measurement of the Higgs boson mass discussed here, will help make the most of the data. We still have much to learn about the Higgs boson, the electroweak theory, and beyond.

Acknowledgments

Fermilab is operated by Fermi Research Alliance, LLC, under Contract No. DE-AC02-07CH11359 with the United States Department of Energy. I thank the Fondation Meyer pour le développement culturel et artistique for generous support.

This research is published in Physical Review Letters.

Correction (18 May 2015): In an earlier version of this article, the axes for Figure 1 were incorrectly labeled. The horizontal axis should say “Top quark mass” and the vertical axis should say “W boson mass”.

References

G. Aad et al. (ATLAS Collaboration), “Observation of a New Particle in the Search for the Standard Model Higgs Boson with the ATLAS Detector at the LHC,” Phys. Lett. B 716, 1 (2012); S. Chatrchyan et al. (CMS Collaboration), “Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC,” Phys. Lett. B 716, 30 (2012)
G. Aad et al. (ATLAS Collaboration, CMS Collaboration), “Combined Measurement of the Higgs Boson Mass in $p p$ Collisions at $\sqrt{s} = 7$ and 8 TeV with the ATLAS and CMS Experiments,” Phys. Rev. Lett. 114, 191803 (2015)
The electroweak theory was developed from a proposal by S. Weinberg, “A Model of Leptons,” Phys. Rev. Lett. 19, 1264 (1967); A. Salam “Weak Electromagnetic Interactions,” in Elementary Particle Theory: Relativistic Groups and Analyticity (Nobel Symposium No. 8), edited by N. Svartholm (Almqvist and Wiksell, Stockholm, 1968), p. 367; http://j.mp/r9dJOo; The theory is built on the SU(2) $_{L} \otimes$ U(1) $_{Y}$ gauge symmetry investigated by S. L. Glashow, “Partial Symmetries of Weak Interactions,” Nucl. Phys. 22, 579 (1961)
C. Quigg, “Electroweak Symmetry Breaking in Historical Perspective,” Ann. Rev. Nucl. Part. Sci. (to be published); arXiv:1503.01756
ATLAS Collaboration, “The ATLAS Experiment at the CERN Large Hadron Collider,” JINST 3, S08003 (2008); CMS Collaboration, “The CMS Experiment at the CERN Large Hadron Collider,” 3, S08004 (2008)
S. Heinemeyer et al. (LHC Higgs Cross Section Working Group), Handbook of LHC Higgs Cross Sections: 3. Higgs Properties, Report No. CERN-2013-004; Tables of Higgs boson branching fractions are given at http://j.mp/1OrjQL0
M. Baak et al. (Gfitter Group), “The global electroweak fit at NNLO and prospects for the LHC and ILC,” Eur. Phys. J. C 74, 3046 (2014); a more detailed version of Figure 1 may be found at http://j.mp/1cvuXGQ
D. Buttazzo, G. Degrassi, P. P. Giardino, G. F. Giudice, F. Sala, A. Salvio, and A. Strumia, ”Investigating the Near-Criticality of the Higgs Boson,” J. High Energy Phys. 1312, 089 (2013)

About the Author

Chris Quigg is Distinguished Scientist Emeritus at the Fermi National Accelerator Laboratory. His research spans many topics in particle physics, from heavy quarks through cosmic neutrinos. His work on electroweak symmetry breaking and supercollider physics, which was recognized by the 2011 J. J. Sakurai Prize of the American Physical Society for outstanding achievement in particle theory, charted the course for exploration at Fermilab’s Tevatron and CERN’s Large Hadron Collider. His current research centers on experiments at the LHC. He is completing a book on particle physics for inquisitive readers. Quigg served as co-chair of Snowmass 2001.