Trapped in a Photonic Maze
Imagine yourself in a huge building, lost in a maze of corridors and trying to find a way out. Imagine further that whatever route you try, you always end up back in the place where you started. Although you can move around, de facto you are trapped, localized in a limited region of space. While this might sound like a surrealistic scenario for a motion picture, it is also a good analogy for how researchers attempt to trap light and other types of waves. Mario Molina and colleagues [1] at the University of Chile, Santiago, and Robert Thomson and colleagues [2] at the Heriot-Watt University in the UK now report how they have trapped light in a crystalline structure called a photonic Lieb lattice [3]. They show that light of a certain frequency can enter a lattice site and remain there, without entering the neighboring sites. The results open up alternative routes to trapping waves.
Waves tend to move at high speed, so trapping them is not straightforward. But they display a property that can be used for confinement: they can interfere with one another. If the structure in which the waves move is made in an appropriate way, interference effects can create a perfect wave trap. Controlling light in structured photonic materials using interference—from controlling its direction, to slowing it down, to trapping it—is a topic of current research [4]. Possible applications of light trapping in such materials abound, including photonic sensors, optical-signal processing, nonlinear optical elements, and microlasers. In addition, good optical traps allow the study of fundamental effects such as the coupling between light and particles in the quantum regime [5].
The beauty of structuring photonic materials to manipulate the flow of light lies in the wealth of properties that can be attained. These range from extreme optical opacity to semitransparency and include a spectral sensitivity that can be broad or peaked at specific wavelengths. To obtain these properties, the material should have structural features that span several length scales. Structures of interest vary between perfectly ordered and fully random, but recent focus has been on structures that also exhibit partial order [6]. A special case is that of a new disordered material called Lévy glass, in which light waves perform a random walk of fractal (noninteger) dimension [7]. The dimensionality of the structures affects their optical properties. Materials that can trap light in a plane and capture light out of the third dimension could become useful for applications such as solar cells [8].
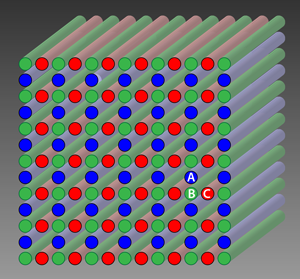
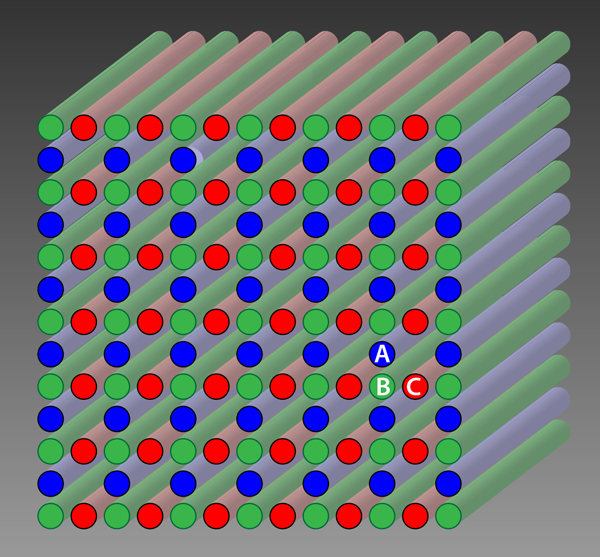
The groups led by Molina and Thomson developed three-dimensional photonic materials that comprise two-dimensional photonic Lieb lattices. The lattices consist of three optical elements ( , , and ) packed in a square pattern but with an empty site at every other site of every other line (Fig. 1). This arrangement allows light to propagate in the third dimension, which is invariant under spatial translation, but localizes it in the plane of the lattice. Using the analogy of you being trapped in a huge building, the structure would consist of a series of parallel (infinite) corridors, in which you could run along one of them and every time you wanted to “change lanes” you would get thrown back. By sending light in from one end of the structure and monitoring how it comes out the other side, the authors showed that in a Lieb lattice such localization occurs only at very specific frequencies; for the remaining part of the frequency spectrum, the light propagates freely in all three directions. The materials can be seen as the analog of an optical fiber that has a single optical mode for certain frequencies and a complex, multimode pattern at all other frequencies.
Light-trapping schemes in which light can freely propagate in one direction have an advantage over other methods. They allow a much easier means of blocking light motion in the other two directions, using materials of only modest refractive index. The same approach was previously used, for instance, in the observation of transverse localization of light [9], in which disorder in two directions blocks propagation but leaves light propagating freely in the third [10]. As in ordered, crystalline structures, interference effects can confine light in disordered media. But the underlying physics of the trapping is much more complex in the disordered case owing to an intricate phenomenon called Anderson localization, which is a general interference phenomenon that allows the formation of random optical modes with a high degree of spatial localization [11].
Engineering materials with structural order and disorder could lead to novel phenomena. It has been predicted, for instance, that ordered photonic crystals with a certain amount of randomness could exhibit a special type of strong localization [12]. The phenomenon is based on the ability of ordered structures to slow down waves in a certain frequency window, which would make it easier for the disordered part of the material to create localized modes. However, so far, experimentalists have not been able to observe this effect. The systems used by Molina’s and Thomson’s groups may offer a way to implement a similar order–disorder localization scheme. A possible approach would be to add disorder to the otherwise ordered Lieb lattice. An alternative method would involve leaving the ordered Lieb lattice untouched and introducing disorder in the third dimension. The disorder would easily produce one-dimensional Anderson localization along the light’s propagation direction. Together with the localization of light in the two-dimensional Lieb lattice, this would provide a complete, three-dimensional light trap.
Overall, the authors’ results provide inspiration for developing alternative light-trapping schemes in structured photonic materials. Such schemes could be used to make optical fibers with particular mode properties, or microscopic optical cavities if propagation in the third dimension can be blocked in a convincing way. On the fundamental physics front, the results could open up new avenues to study the interplay between order and disorder in photonics.
This research is published in Physical Review Letters.
References
- Rodrigo A. Vicencio, Camilo Cantillano, Luis Morales-Inostroza, Bastián Real, Cristian Mejía-Cortés, Steffen Weimann, Alexander Szameit, and Mario I. Molina, “Observation of Localized States in Lieb Photonic Lattices,” Phys. Rev. Lett. 114, 245503 (2015)
- Sebabrata Mukherjee, Alexander Spracklen, Debaditya Choudhury, Nathan Goldman, Patrik Öhberg, Erika Andersson, and Robert R. Thomson, “Observation of a Localized Flat-Band State in a Photonic Lieb Lattice,” Phys. Rev. Lett. 114, 245504 (2015)
- E. H. Lieb, “Two Theorems on the Hubbard Model,” Phys. Rev. Lett. 62, 1201 (1989)
- D. S. Wiersma, “Disordered Photonics,” Nature Photon. 7, 188 (2013)
- M. Brune, F. Schmidt-Kaler, A. Maali, J. Dreyer, E. Hagley, J. M. Raimond, and S. Haroche, “Quantum Rabi Oscillation: A Direct Test of Field Quantization in a Cavity,” Phys. Rev. Lett. 76, 1800 (1996)
- M. Florescu, S. Torquato, and P. J. Steinhardt, “Designer Disordered Materials with Large, Complete Photonic Band Gaps,” Proc. Natl. Acad. Sci. U.S.A. 106, 20658 (2009)
- P. Barthelemy, J. Bertolotti, and D.S. Wiersma, “A Lévy Flight for Light,” Nature 453, 495 (2008)
- M. D. Kelzenberg et al., “Enhanced Absorption and Carrier Collection in Si Wire Arrays for Photovoltaic Applications,” Nature Mater. 9, 239 (2010)
- H. de Raedt, A. Lagendijk, and P. de Vries, “Transverse Localization of Light,” Phys. Rev. Lett. 62, 47 (1989)
- T. Schwartz, G. Bartal, S. Fishman, and M. Segev, “Transport and Anderson Localization in Disordered Two-Dimensional Photonic Lattices,” Nature 446, 52 (2007)
- E. Akkermans and G. Montambaux, Mesoscopic Physics of Electrons and Photons (Cambridge University Press, Cambridge, 2007)[Amazon][WorldCat]
- S. John and Electromagnetic Absorption in a Disordered Medium near a Photon Mobility Edge, ” Phys. Rev. Lett. 53, 2169 (1984)