Rescuing the Quasiparticle

Jean-Philippe Reid

Viewpoint

Rescuing the Quasiparticle

School of Physics & Astronomy, University of St Andrews, North Haugh, St Andrews KY16 9SS, United Kingdom

July 20, 2015• Physics 8, 70

Experiments with heavy-fermion materials show that quasiparticles exist at the critical point of a quantum phase transition.

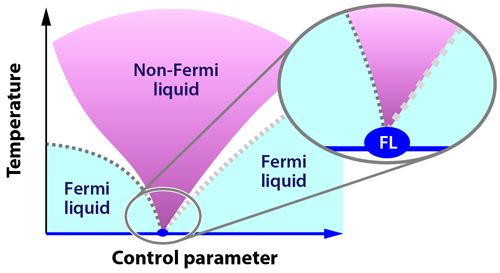
Figure caption — **Figure 1:** A phase diagram for a material with a phase transition at zero temperature. The unstable point between these two phases, the quantum critical point (QCP), is indicated here by the dark blue point. Experiments have shown that Fermi-liquid theory (FL), the standard framework for describing interacting electrons in a material, does not describe the properties of materials near a QCP (purple region). But Taupin *et al.* and Sutherland *et al.* have made the surprising finding that Fermi-liquid theory is valid at the QCP.

We can turn water into a chaotic cloud of steam or a perfectly ordered cube of ice simply by varying temperature or pressure. These “classical” phase transitions are governed by thermal fluctuations, which affect the entropy and total energy of a system. Phase transitions can, however, also occur at zero temperature, where thermal fluctuations are nonexistent. Here, the only available fluctuations are quantum fluctuations, and the unstable boundary between two phases is known as a quantum critical point (QCP). QCPs are of interest because they can be associated with certain unusual forms of superconductivity. But it is unclear whether we can describe QCPs using Fermi-liquid theory, the framework that works so well for predicting the properties of most metals and semiconductors. Indeed, experiments have shown that Fermi-liquid theory breaks down tens of kelvins or more above a QCP (Fig. 1). But as two research groups now show with low-temperature experiments, the theory regains its footing at the QCP [1,2]. The results thus provide new constraints for physicists as they develop a theoretical description for materials near a quantum phase transition.

The study of quantum phase transitions took off in 1975, with the discovery of heavy-fermion compounds [3]. These materials are usually formed from actinide or rare-earth elements. Their electrons interact strongly with each other and therefore behave as if they have an enormous effective mass, hundreds or even a thousand times greater than the mass of a free electron. These electrons with a renormalized mass are often called quasiparticles, and Fermi-liquid theory rests on the assumption that they exist.

Most heavy fermion materials possess an antiferromagnetic phase below a certain temperature ( $T_{N}$ ), which can persist at absolute zero if a control parameter, such as pressure or magnetic field, is applied. What physicists find so intriguing about these materials is that they have a magnetic QCP, close to which quantum fluctuations prevent long-range antiferromagnetic order, and novel phases such as superconductivity become energetically favorable [4,5].

Among the models that have been proposed to describe this instability, one stands apart called the “local quantum critical scenario” [6]. Within this model, quantum fluctuations at the QCP are so strong that it is no longer possible to describe particles with a renormalized mass—they are just too heavy—and the whole concept of quasiparticle, and hence Fermi-liquid theory, breaks down.

One of the best tests of whether quasiparticles exist is to verify the Wiedemann-Franz law. This pillar of Fermi-liquid theory stipulates that, in the limit of zero temperature, the ratio of the electronic part of the thermal conductivity carried by charges ( $κ_{e}$ ) to the electrical conductivity ( $σ$ ) is a universal constant, $L_{0}$ . One of the key assumptions of this law, however, is that heat and charge are transported by the same particle (or quasiparticle). Observing a deviation from the Wiedemann-Franz ratio at zero temperature in a material would therefore imply that a material’s physics cannot be described within the quasiparticle picture.

In the past several years, three independent groups have tested the Wiedemann-Franz law in the heavy fermion material ${YbRh}_{2} {Si}_{2}$ near its QCP. (In ${YbRh}_{2} {Si}_{2}$ , the QCP separates an antiferromagnetic phase from a paramagnetic phase; the phase transition can be driven by applying an external magnetic field.) But the team have drawn contradictory conclusions. One group claims the Wiedemann-Franz law is violated [7], whereas the other two groups (including one that I am a former member of) find the law describes measurements well [8,9]. The origin of this disagreement lies in how the three groups account for the appearance, at low temperatures, of excitations called magnons. These excitations only contribute to the thermal conductivity, and their contribution must be precisely known in order to test the Wiedemann-Franz law at the QCP. To settle this debate, one needs to know the exact magnon contribution to the thermal conductivity, or test the Wiedemann-Franz law at much lower temperatures, where the magnon contribution becomes negligible.

Mathieu Taupin from the Université Grenoble Alpes in France and colleagues take the latter approach [1]. Focusing on the same material, ${YbRh}_{2} {Si}_{2}$ , they measure both heat and charge transport down to $10$ millikelvin ( $mK$ ) in the antiferromagnetic phase, at the QCP, and in the paramagnetic phase. Measuring heat propagation through a crystal a few milikelvin above absolute zero is an experimental tour de force: they have to apply enough heat to cause a temperature gradient, but not so much that the sample’s average temperature increases significantly. The authors show the magnon contribution appears below $30 mK$ and persists beyond the QCP. Then, by focusing only on the electronic part of the thermal conductivity, the authors show that the ratio of $L (T) / L_{0}$ converges, with decreasing temperature, to $97 %$ not only at the QCP but also in the magnetic phases on either side of the QCP. Their measurements make a strong case that the Wiedemann-Franz law applies near the QCP of ${YbRh}_{2} {Si}_{2}$ . But the authors acknowledge that only further measurements below $10 mK$ , where the magnon contribution is negligible, could really settle this debate.

Michael Sutherland from the University of Cambridge and colleagues report a similar measurement, but on the heavy fermion material $β$ - ${YbAlB}_{4}$ [2]. Studying this material has the advantage that its quasiparticles become heavy at a relatively high temperature. In fact, the relevant temperature scale, called the Kondo temperature, $T_{K}$ , is eight times greater than it is for ${YbRh}_{2} {Si}_{2}$ . In this case, unlike ${YbRh}_{2} {Si}_{2}$ , the authors’ measurements deliver clear evidence that the Wiedemann-Franz law is valid at the QCP. In fact, they are able to test the Wiedemann-Franz law extremely close to the QCP ( $T / T_{K} ≅ 0.00035$ ), a limit never achieved before.

The conclusion of these studies and their implications are truly significant: any theoretical framework that attempts to describe these quantum phase transitions will have to account for deviations of the Fermi-liquid theory visible tens of kelvins above the QCP, and reinstate it at zero temperature. ${CeCoIn}_{5}$ is the one heavy fermion compound known to violate the Wiedemann-Franz law [10]. This is, however, based on measurements performed as low as $50 mK$ , and we cannot exclude the possibility that the Wiedemann-Franz law might again be valid at lower temperature. Perhaps Taupin and his collaborators could try to reproduce these measurements down to $10 mK$ .

This research is published in Physical Review Letters and as a Rapid Communication in Physical Review B.

References

M. Taupin, G. Knebel, T. D. Matsuda, G. Lapertot, Y. Machida, K. Izawa, J.-P. Brison, and J. Flouquet, “Thermal Conductivity through the Quantum Critical Point in ${YbRh}_{2} {Si}_{2}$ at Very Low Temperature,” Phys. Rev. Lett. 115, 046402 (2015)
M. L. Sutherland, E. C. T. O’Farrell, W. H. Toews, J. Dunn, K. Kuga, S. Nakatsuji, Y. Machida, K. Izawa, and R. W. Hill, “Intact quasiparticles at an unconventional quantum critical point,” Phys. Rev. B 92, 041114 (2015)
K. Andres, J. E. Graebner, and H. R. Ott, “ $4 f$ -Virtual-Bound-State Formation in CeAl $_{3}$ at Low Temperatures,” Phys. Rev. Lett. 35, 1779 (1975)
F. Steglich, J. Aarts, C. D. Bredl, W. Lieke, D. Meschede, W. Franz, and H. Schäfer, “Superconductivity in the Presence of Strong Pauli Paramagnetism: CeCu $_{2}$ Si $_{2}$ ,” Phys. Rev. Lett. 43, 1892 (1979)
N. D. Mathur, F. M. Grosche, S. R. Julian, I. R. Walker, D. M. Freye, R. K. W. Haselwimmer, and G. G. Lonzarich, “Magnetically Mediated Superconductivity in Heavy Fermion Compounds,” Nature 394, 39 (1998)
P. Gegenwart, Q. Si, and F. Steglich, ”Quantum Criticality in Heavy-Fermion Metals,” Nature Phys. 4, 186 (2008)
H. Pfau et al., “Thermal and Electrical Transport Across a Magnetic Quantum Critical Point,” Nature 484, 493 (2012)
Y. Machida, K. Tomokuni, K. Izawa, G. Lapertot, G. Knebel, J.-P. Brison, and J. Flouquet, “Verification of the Wiedemann-Franz Law in YbRh $_{2}$ Si $_{2}$ at a Quantum Critical Point,” Phys. Rev. Lett. 110, 236402 (2013)
J.-Ph. Reid, M. A. Tanatar, R. Daou, R. Hu, C. Petrovic, and L. Taillefer, “Wiedemann-Franz Law and Nonvanishing Temperature Scale across the Field-Tuned Quantum Critical Point of YbRh $_{2}$ Si $_{2}$ ,” Phys. Rev. B. 89, 045130 (2014)
M. A. Tanatar, J. Paglione, C. Petrovic, and L. Taillefer, “Anisotropic Violation of the Wiedemann-Franz Law at a Quantum Critical Point,” Science 316, 1320 (2007)

About the Author

Jean-Philippe Reid received his Ph.D. from the University of Sherbrooke in 2012 and then joined the School of Physics and Astronomy at the University of St Andrews as a postdoctoral fellow. He is mainly interested in how magnetic properties of quantum materials can provide new exotic phases such as superconductivity.