Cool and Heavy

Lin Tian

Viewpoint

Cool and Heavy

School of Natural Sciences, University of California, Merced, CA 95343, USA

January 26, 2015• Physics 8, 8

A new scheme for cooling a mechanical oscillator in a cavity may allow the observation of quantum effects on macroscopic objects and the realization of ultrasensitive gravitational-wave detectors.

Figure caption — **Figure 1:** Scheme of the optomechanical setup used by Sawadsky *et al.* [2]. Laser light circulates in a cavity formed by a Michelson-Sagnac interferometer and a high reflectivity signal-recycling mirror (SRM). The Michelson-Sagnac interferometer contains a silicon nitride membrane ( $SiN$ ), which acts as a mechanical oscillator with a fundamental frequency of $136$ kilohertz. The $SiN$ membrane can control both the cavity frequency (dispersive coupling) and its bandwidth (dissipative coupling). With a proper balance of the two coupling forms, the laser light cools the mechanical oscillator to an effective temperature of $111$ millikelvin.

Cavity optomechanics studies the interaction between light and mechanical systems, most often mediated by radiation pressure—the force exerted by photons hitting on a mirror. In a typical optomechanics setup, microwave or optical photons travel in a cavity formed by two or more mirrors, one of which is free to move and acts like a mechanical oscillator whose position changes because of radiation pressure and thermal fluctuations. A recent milestone in the field was the cavity cooling of mechanical oscillators to a regime in which they have less than one quantum of motion [1]. This could have important applications, ranging from the observation of quantum behavior in macroscopic systems to the development of ultrasensitive detectors that could reveal the tiny vibrations caused by the still-elusive gravitational waves. However, to-date-demonstrated schemes require that the frequency of the cooling light be lower than the cavity resonant frequency by an amount corresponding to the frequency of the mechanical oscillator. These two frequencies can be measurably different only if the oscillator’s frequency is sufficiently large. This poses an important limitation, as low frequency, heavy oscillators cannot be cooled by this method.

Now a team led by Roman Schnabel at the Albert Einstein Institute in Hannover, Germany has reported an optomechanical cooling scheme that gets rid of this frequency-detuning requirement [2]. The key to their achievement is a novel form of optomechanical coupling. Optomechanics has been mainly investigated using “dispersive coupling,” in which displacements of the oscillating mirror change the resonant frequency of the cavity [3]. Here, the authors rely instead on “dissipative coupling,” in which the mirror oscillations modify the coupling between the cavity and its environment, for instance by modulating the speed at which cavity photons are lost (i.e., the cavity bandwidth).

In the dispersive coupling regime, the most widely used cooling approach is “cavity cooling” [3]. In this method, light cools a mechanical mode via a “parametric” process: quanta of mechanical excitations are up-converted into cavity photons, which are then dissipated through the cavity. The light frequency must be detuned from the cavity resonant frequency: the mechanical oscillator produces lower-frequency (red) and higher-frequency (blue) sidebands, which are shifted from the cavity resonance by multiples of the mechanical frequency $ω_{M}$ . When the driving frequency is tuned to the first red sideband, photons entering the cavity take away phonons with energy $ħ ω_{M}$ from the mechanical system, cooling the oscillator. In a number of previous studies, this method allowed researchers to bring mechanical oscillators to their quantum ground state (i.e., states in which the average number of mechanical excitations is reduced below unity) [1] and to realize the coherent conversion of photons to mechanical motion and of microwave photons to optical photons [4]. But these realizations required the system to be in the “resolved sideband regime”: for the red sideband to be distinguishable from the cavity frequency, the frequency of the mechanical oscillator (determining the shift of the sidebands) has to be larger than the cavity bandwidth. Ground-state cooling has been achieved for frequencies down to hundreds of megahertz, but reaching lower frequencies (such as the $\sim 100$ -kilohertz frequency of the mechanical resonator used by Schnabel’s team) would require cavities with extremely narrow bandwidths, which are currently not available.

However, a recent theory shows that cavity cooling could be possible without the requirement to resolve the mechanical-oscillator sidebands [5] if the optomechanical coupling is dissipative [6]. In dissipatively coupled systems, two types of fluctuating forces act on the mechanical resonator: the noise in the light injected into the cavity and the quantum fluctuation of the cavity field. These two types of noise, which have different spectra, can interfere destructively. With proper parameter choice, such interference can reduce the spectral density of the noise at the frequency $(- ω_{M})$ of the oscillator, effectively cooling it. This mechanism, which does not require to resolve the sidebands, can work with a low oscillator frequency.

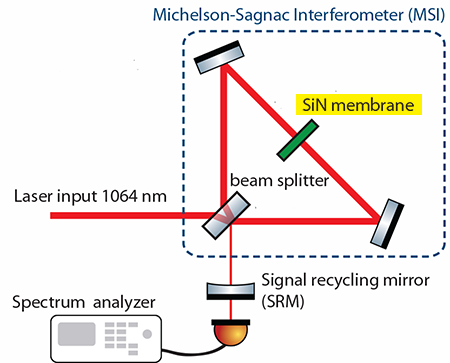
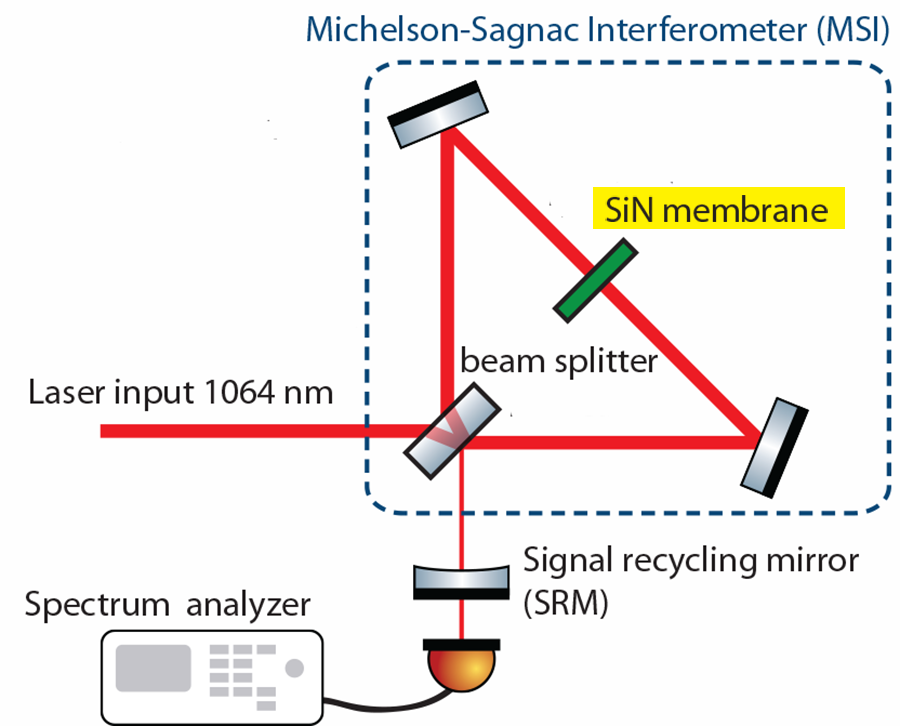
Here the authors use dissipative coupling in tandem with dispersive coupling to demonstrate experimentally a general form of optomechanical cooling. In their setup (see Fig. 1) the optical cavity is formed by a Michelson-Sagnac interferometer (in which light, divided by a beam splitter, propagates in two different directions of a ring cavity) and a highly reflective “signal-recycling” mirror placed at the interferometer’s output [7]. This mirror serves as a way to adjust the cavity resonance and, by sending some light back to the interferometer, amplifies the light field in the cavity. Inside the interferometer, a movable silicon nitride membrane acts as the mechanical oscillator of interest, with a fundamental frequency of $136$ kilohertz. Its position modifies both the amount of light inside the cavity and that emitted from the output port, thereby affecting the bandwidth as well as the resonant frequency of the cavity. It is through this membrane that dispersive coupling (i.e., modulation of the cavity frequency) and dissipative couplings (i.e., modulation of the cavity bandwidth) are realized. In the experiment, the cavity bandwidth is tunable between $0.7$ and $1.5$ megahertz and is much larger than the mechanical oscillator frequency.

In stark contrast to dispersive-coupling systems, Schnabel et al.’s experiments demonstrate cooling of the mechanical oscillator over a wide detuning range, below and above the cavity resonance. Most importantly, cooling can be driven by a light source with a frequency arbitrarily close to the cavity resonance. The setup could thus cool heavy mechanical oscillators with low frequencies. The authors measured the effective temperature of the oscillating membrane by monitoring the noise of its displacement. From an initial thermal temperature of $300$ kelvin, the mechanical mode reached an effective thermal temperature of $111$ millikelvin, a three-orders-of-magnitude reduction of the thermal occupation of the mechanical mode.

The scheme of Schnabel et al. opens new avenues for realizing optomechanical cooling schemes that are relevant to a number of research fields. First, it might allow increasingly heavy mirrors to be cooled to their quantum ground states, opening the door for the testing of quantum effects on macroscopic scales [3]: Oscillators made of billions of atoms could be entangled or prepared in a superposition of quantum states, realizing, for instance, macroscopic “Schrödinger cats.” Second, since mechanical motion can affect the electromagnetic energy stored in a system, mechanical resonators could be coupled to a variety of quantum systems, such as superconducting qubits, cold atoms, and semiconductor microcavities. They could thus serve as a medium to connect devices working at very different frequency ranges, facilitating the construction of hybrid quantum information systems [4]. But one of the most intriguing applications would be in gravitational wave (GW) detection. The “advanced LIGO” experiment [8], an upcoming extension of LIGO (Laser Interferometer Gravitational-Wave Observatory), will use a similar interferometric setup formed by a Michelson interferometer and a signal-recycling mirror. In such a system, a test mass would serve as a mechanical oscillator that could sense gravitational waves. It has been predicted [9] that the optical field in the cavity would produce an “optical spring” that acts on the mass just like an elastic spring, increasing the sensitivity of the detector. Unfortunately, further work [7] has shown that, for purely dispersive optomechanical coupling, such an optical spring would be inherently unstable, leading to uncontrollable mechanical oscillations. But this issue could be avoided by adding dissipative coupling, using its interplay with dispersive couplings to stabilize the mechanical oscillator [7]. The new experimental demonstration could thus enable an important route towards more sensitive gravitational wave detectors.

This research is published in Physical Review Letters.

References

J. Chan, T. P. Mayer Alegre, A. H. Safavi-Naeini, J. T. Hill, A. Krause, S. Gröblacher, M. Aspelmeyer, and O. Painter, “Laser Cooling of a Nanomechanical Oscillator into its Quantum Ground State,” Nature 478, 89 (2011); J. D. Teufel, T. Donner, Dale Li, J. W. Harlow, M. S. Allman, K. Cicak, A. J. Sirois, J. D. Whittaker, K. W. Lehnert, and R. W. Simmonds, “Sideband Cooling of Micromechanical Motion to the Quantum Ground State,” ibid. 475, 359 (2011); E. Verhagen, S. Deléglise, S. Weis, A. Schliesser, and T. J. Kippenberg, “Quantum-Coherent Coupling of a Mechanical Oscillator to an Optical Cavity Mode,” ibid. 482, 63 (2012)
Andreas Sawadsky, Henning Kaufer, Ramon Moghadas Nia, Sergey P. Tarabrin, Farid Ya. Khalili, Klemens Hammerer, and Roman Schnabel, “Observation of Generalized Optomechanical Coupling and Cooling on Cavity Resonance,” Phys. Rev. Lett. 114, 043601 (2015)
M. Aspelmeyer, T. J. Kippenberg, and F. Marquardt, “Cavity Optomechanics,” Rev. Mod. Phys. 86, 1391 (2014)
L. Tian, “Optoelectromechanical Transducer: Reversible Conversion Between Microwave and Optical Photons,” Ann. Phys. (Berlin) 527, 1 (2015)
F. Elste, S. M. Girvin, and A. A. Clerk, “Quantum Noise Interference and Backaction Cooling in Cavity Nanomechanics,” Phys. Rev. Lett. 102, 207209 (2009)
M. Li, W. H. P. Pernice, and H. X. Tang, “Reactive Cavity Optical Force on Microdisk-Coupled Nanomechanical Beam Waveguide,” Phys. Rev. Lett. 103, 223901 (2009); M. Wu, A. C. Hryciw, C. Healey, D. P. Lake, H. Jayakumar, M. R. Freeman, J. P. Davis, and P. E. Barclay, “Dissipative and Dispersive Optomechanics in a Nanocavity Torque Sensor,” Phys. Rev. X 4, 021052 (2014)
S. P. Tarabrin, H. Kaufer, F. Y. Khalili, R. Schnabel, and K. Hammerer, “Anomalous Dynamic Backaction in Interferometers,” Phys. Rev. A 88, 023809 (2013)
Information on the LIGO project and related publications can be found at http://www.ligo.org.
A. Buonanno, and Y. Chen, “Signal Recycled Laser-Interferometer Gravitational-Wave Detectors as Optical Springs,” Phys. Rev. D 65, 042001 (2002)

About the Author

Lin Tian received her Ph.D. in physics (2002) from the Massachusetts Institute of Technology. She then worked as postdoc researcher at Universität Innsbruck, NIST at Gaithersburg, and Stanford University. She is now an Associate Professor of Physics at the University of California, Merced. She works on theoretical questions in quantum optomechanics, quantum simulation, and decoherence models.