Signs of a Gardner Transition in a Granular Glass
The glass transition, in which materials become so viscous that they cannot flow even on extremely long time scales, has baffled scientists for over one hundred years. Experiments have shown that the viscosity can increase in atomic and polymeric liquids by more than 15 orders of magnitude—think of going from the viscosity of water to that of asphalt—over a narrow range of decreasing temperature without a significant increase in crystalline order. In addition to occurring in simple liquids, the glass transition has also been observed in colloids [1], metals [2], and biological systems such as the cytoplasm of cells [3] and tissues [4]. Some of the most basic questions concerning the glass transition remain open. For example, is there a true phase transition at a nonzero temperature to an “ideal glass” characterized by infinite viscosity, or do glassy materials simply become more and more sluggish as the temperature decreases to zero? Without answers to these questions, it is extremely difficult to predict the structural, mechanical, and rheological properties of glasses. The lack of a theoretical framework for glasses has impeded their widespread use in industry.
Perhaps insight into the glass transition could come from a related transition known as the jamming transition. Jamming typically occurs in systems without thermal fluctuations, such as granular materials, which are composed of macroscale grains that interact via frictional contact forces. As their packing fraction (the proportion of space occupied by the grains) is increased, these systems jam, meaning they become mechanically stable because the forces and torques on each grain sum to zero. An interesting question is whether the glass transition can be considered as a type of jamming transition in which the viscosity diverges at a nonzero temperature, particle motion stops, and the system becomes a disordered solid. Or are these two transitions fundamentally different? In a new study [5], Antoine Seguin and Olivier Dauchot from the French National Center for Scientific Research (CNRS) provide evidence for the existence of a new phase transition—the Gardner transition—that happens between the glass and jamming transitions in a granular system composed of hard particles. At this transition, basins in the energy landscape of the materials divide into many subbasins. The transition was originally predicted to occur in energy-conserving, hard-sphere systems in high spatial dimensions (much above three dimensions). However, Seguin and Dauchot found signatures of the transition in highly dissipative granular materials in only two dimensions. This result implies that the current, “mean-field” theoretical description of the transition may apply to physically realizable spatial dimensions.
Significant theoretical advances [6, 7] have been made in understanding glass and jamming transitions in model systems composed of hard spheres in high spatial dimensions, in which it is easier to perform calculations. In hard-sphere systems, interparticle overlaps are prohibited, and the packing fraction 𝜑 alone determines both the glass and jamming transitions. These studies have shown that the glass transition, in which particles become trapped in cages formed by neighboring particles, occurs at a packing fraction 𝜑g that is below that of the jamming transition 𝜑J. Glasses with 𝜑g<𝜑<𝜑J are trapped within a local region of configuration space, but are not yet mechanically stable. These studies have also identified another characteristic packing fraction, 𝜑G, with 𝜑g<𝜑G<𝜑J, that marks the Gardner transition, above which glass configurations can be compressed further into one of many closely spaced but distinct mechanically stable packings. Thus a signature of the Gardner transition would be the ability to compress packings with 𝜑>𝜑g to a large set of distinct jammed packings.
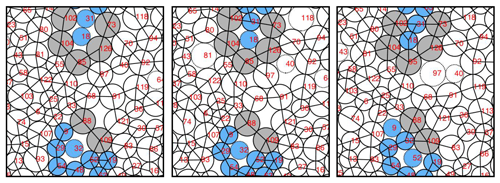
Seguin and Dauchot describe an ingenious experiment to explore the slow dynamics of glassy materials in the range of packing fractions 𝜑g<𝜑G<𝜑J. They consider a quasi-two-dimensional (2D) cell filled with thin cylindrical grains that can be compressed from the sides in small steps, with each compression step followed by a series of horizontal vibrations. This setup allows tracking of all particles in the cell and measurement of two quantities to detect signatures of the Gardner transition: the mean-square displacement Δ(𝜑) of particles from a single compression and vibration run, and the mean-square displacement ΔAB(𝜑) of corresponding particles in two configurations, A and B, that were prepared at the same initial packing fraction 𝜑0>𝜑g and then compressed and vibrated independently.
The authors find that, for 𝜑<0.82, Δ(𝜑)≈ΔAB(𝜑) and both decrease with increasing 𝜑. In this regime, the differences between configurations in a single run and those from different runs are comparable. However, for 𝜑>0.82, ΔAB(𝜑) no longer decreases and instead it reaches a plateau ΔAB≈10−2. (A similar value for the distance between distinct disk packings was found in Ref. [8].) The small, nonzero value of ΔAB suggests that for 𝜑>0.82, but below the onset of jamming, there can be small differences between mechanically stable configurations started at the same 𝜑0 (Fig. 1) that are much larger than Δ(𝜑) for single configurations, which tends to zero as the system approaches jamming onset. For this reason, the authors identified 0.82 with 𝜑G of the Gardner transition.
Seguin and Dauchot also investigated the slow time evolution of Δ(𝜑) and ΔAB(𝜑). Consistent with theoretical studies, they provide evidence that Δ(𝜑) and ΔAB(𝜑) depend strongly on the number and duration of the horizontal vibrations only for 𝜑>𝜑G. This suggests that the system can move among nearby mechanically stable packings in this regime. In contrast, for 𝜑g<𝜑<𝜑G, Δ(𝜑) and ΔAB(𝜑) are not sensitive to the degree of shaking, which suggests that the system cannot access multiple nearby packings in this regime.
The authors’ study presents the first experimental results that point to the existence of a Gardner-like transition in glassy systems in 2D. But a number of questions concerning the role of the Gardner transition remain open. The first question involves the consequences of “rattler” particles, which do not participate in the force-bearing contact network of mechanically stable packings for 𝜑>𝜑G. When a system is decompressed from jamming onset and vibrated, such rattlers can destabilize the original mechanically stable packing, causing the system to transition to another packing. Further, rattlers can be incorporated into the force-bearing contact network of the new packing (see Fig. 1.) The effects of rattler particles have not been considered in the mean-field theoretical description of the Gardner transition, yet they will influence the counting of mechanically stable packings and the characterization of the transitions between them.
Seguin and Dauchot’s study focused on packings of frictional grains. However, since the grains were vibrated after each small compression step, the particles frequently came in and out of contact with their neighbors, which released the frictional forces. A previous study [9] has shown that the number and organization of mechanically stable packings of frictional particles is very different from that for frictionless particles. Therefore, an important topic for future research is to consider how frictional interparticle forces affect the Gardner transition in granular glasses.
By showing signatures of the Gardner transition in a regime between the glass and jamming transitions, Seguin and Dauchot’s work emphasizes key differences between these transitions in hard-sphere-like systems. The glass transition signals the localization of the system into a basin in the energy landscape. The Gardner transition indicates the partitioning of this basin into a series of distinct subbasins. And the jamming transition occurs when the system resides in the minimum of one of these subbasins. In addition, this work will encourage new studies aimed at determining how more realistic particle interactions, particle shapes, and dynamics influence the glass, jamming, and Gardner transitions.
This research is published in Physical Review Letters.
References
- E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield, and D. A. Weitz, “Three-Dimensional Direct Imaging of Structural Relaxation Near the Colloidal Glass Transition,” Science 287, 627 (2000).
- S. Mukherjee, J. Schroers, W. L. Johnson, and W.-K. Rhim, “Influence of Kinetic and Thermodynamic Factors on the Glass-Forming Ability of Zirconium-Based Bulk Amorphous Alloys,” Phys. Rev. Lett. 94, 245501 (2005).
- B. R. Parry, I. V. Surovtsev, M. T. Cabeen, C. S. O’Hern, E. R. Dufresne, and C. Jacobs-Wagner, “The Bacterial Cytoplasm has Glass-like Properties and is Fluidized by Metabolic Activity,” Cell 156, 183 (2014).
- D. Bi, X. Yang, M. C. Marchetti, and M. L. Manning, “Motility-Driven Glass and Jamming Transitions in Biological Tissues,” Phys. Rev. X 6, 021011 (2016).
- A. Seguin and O. Dauchot, “Experimental Evidence of the Gardner Phase in a Granular Glass,” Phys. Rev. Lett. 117, 228001 (2016).
- P. Charbonneau, Y. Jin, G. Parisi, C. Rainone, B. Seoane, and F. Zamponi, “Numerical Detection of the Gardner Transition in a Mean-Field Glass Former,” Phys. Rev. E 92, 012316 (2015).
- P. Charbonneau, J. Kurchan, G. Parisi, P. Urbani, and F. Zamponi, “Fractal Free Energy Landscapes in Structural Glasses,” Nature Commun. 5, 3725 (2014).
- G.-J. Gao, J. Blawzdziewicz, C.S. O’Hern, and M. Shattuck, “Experimental Demonstration of Nonuniform Frequency Distributions of Granular Packings,” Phys. Rev. E 80, 061304 (2009).
- T. Shen, S. Papanikolaou, C. S. O’Hern, and M. D. Shattuck, “Statistics of Frictional Families,” Phys. Rev. Lett. 113, 128302 (2014).