Half-Quantum Vortices in Superfluid Helium

James A. Sauls

Viewpoint

Half-Quantum Vortices in Superfluid Helium

Department of Physics and Astronomy, Northwestern University, Evanston, IL 60208, USA

December 14, 2016• Physics 9, 148

Researchers working with superfluid helium in a porous medium have generated vortices with half the quantum unit of fluid flow.

Figure caption — **Figure 1:** In superfluid helium-3, different types of quantum vortices can be observed. (Left) A “normal” vortex, or single quantum vortex, around which the circulation is equal to $h ∕ 2 m$ . This corresponds to a change of $2 𝜋$ in the quantum phase $𝜗$ . By contrast, the phase $𝛼$ , related to the spin direction $\vec{d}$ , remains fixed. (Right) A half quantum vortex has a circulation of $h ∕ 4 m$ . Both $𝜗$ and $𝛼$ change by $𝜋$ to give a total phase change of $2 𝜋$ .

A quantum vortex in a superfluid is a point-like hole around which the superfluid flows. This flow is quantized in the sense that the circulation—which is the sum of the velocity along a path around the vortex—takes on discrete values [1]. The quantum unit of circulation is $h ∕ m$ , where $h$ is Planck’s constant and $m$ is the mass of the superfluid particles. The first detection of quantized vortices with unit circulation were made in the 1960s with superfluid helium-4 and then later in superfluids of the lighter isotope helium-3 [2]. However, in the 1970s theorists predicted the existence of vortices with half of a quantum unit of circulation in superfluid helium-3 [3]. Since then, researchers have detected half-quantum vortices (HQVs) in diverse condensed-matter systems, from Bose-Einstein condensates to spin-triplet superconductors thought to be electronic analogs of superfluid helium-3 [4]. But the search for HQVs in superfluid helium-3 has proven more difficult. Samuli Autti from the Low Temperature Laboratory at Aalto University in Finland and colleagues have succeeded in creating HQVs in a new superfluid phase of helium-3 in a confined geometry [5]. This discovery of superfluid HQVs—40 years in the making—is a testament to a deep theoretical understanding and exquisite control available to the quantum phases of superfluid helium-3. It provides a unique platform for future developments in quantum-state control of a topological phase of quantum matter.

Superfluids are quantum phases of matter in which the atoms condense into a single macroscopically occupied quantum state; i.e., the matter as a whole is described by a complex wave function $Ψ = | Ψ | exp (i 𝜗)$ , defined by an amplitude $| Ψ |$ and phase $𝜗$ . Only bosons are capable of this sort of condensation, so in the case of Fermi liquids like helium-3, the (fermionic) spin-1/2 atoms bind together as (bosonic) Cooper pairs. Mass flow is described by the velocity field of the Cooper pairs, which is proportional to the gradient of the phase $\vec{\nabla} 𝜗$ . For a smoothly varying phase, the flow is irrotational, meaning the circulation is zero along any enclosed path. But when placed in a rotating vessel, superfluids rotate by “perforating the condensate” with lines on which the wave function vanishes. These lines define singularities, or “phase vortices,” for which the phase change around a closed path $C$ is nonzero: $Δ 𝜗 = \oint \vec{\nabla} 𝜗 \cdot d \vec{l} = 2 𝜋 N_{C}$ . The winding number $N_{C}$ must be an integer in order to ensure that the wave function does not change its value after a trip around the vortex. Translating this phase requirement to the velocity field, one can see that the fluid circulation is quantized with the elementary quantum of circulation given by $h ∕ 2 m$ , where $2 m$ is the mass of the two helium atoms in the Cooper pair [1].

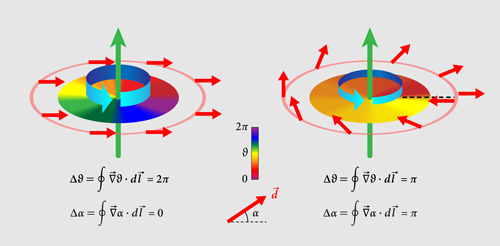
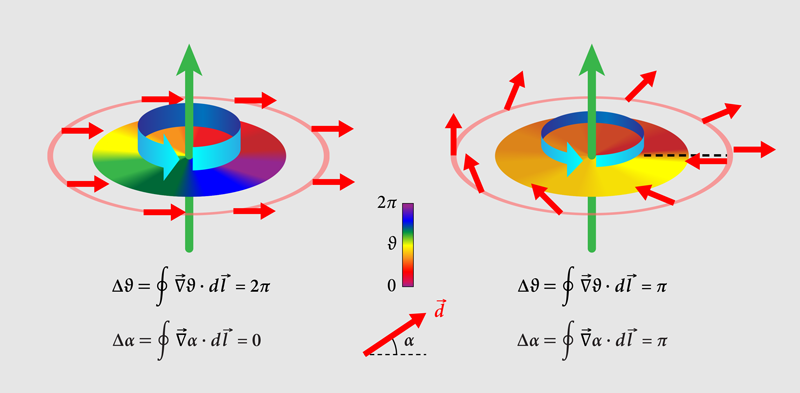
In superfluid helium-3, vortices can have half a quantum of circulation, i.e., $h ∕ 4 m$ , or a phase winding of $Δ 𝜗 = 𝜋$ [3]. How is this possible when it seems to violate the requirement that $Ψ$ be single valued? The answer is that there is a “hidden half” to the topology of the HQV—an extra $𝜋$ twist—that is not related to circulation of the mass current but rather to circulation of spin current.

As mentioned, superfluid helium-3 contains Cooper pairs that are composite bosons with orbital angular momentum $L = 1$ and total nuclear spin $S = 1$ . The latter is comprised of the two spin-1/2 helium-3 nuclei. For unconfined superfluid helium-3, the orientation of the orbital and spin angular momenta are unfavorable to the formation of HQVs. However, researchers recently discovered a new phase of helium-3 when it is confined in nafen—a highly porous aerogel with long parallel strands [6]. The new so-called “polar phase” is a particular realization in which the Cooper pairs are preferentially aligned along the strands of the aerogel [7]. The corresponding spin state is an equal amplitude superposition of Cooper pairs with opposite spin projections. The full wave function is written as $| Ψ 〉 = | Ψ | e^{i 𝜗} (e^{i 𝛼} | ↓ ↓ 〉 - e^{- i 𝛼} | ↑ ↑ 〉)$ . The phase angle $𝛼$ between the two components of the spin state of the Cooper pairs is the “hidden” phase allowing superfluid helium-3 to accommodate HQVs. The HQV with $Δ 𝜗 = 𝜋$ is realized by including a $𝜋$ phase change in the spin components: $Δ 𝛼 = 𝜋$ (see Fig. 1).

The spin state is simply visualized as a vector $\vec{d} = cos 𝛼 \hat{x} + sin 𝛼 ŷ$ confined in the plane perpendicular to the quantization axis for the $| ↑ ↑ 〉$ spinor. In a “normal” full-unit vortex (called a single-quantum vortex), the vector $\vec{d}$ is fixed. But for an HQV, $\vec{d}$ rotates, generating a spin current around the vortex.

In their experiments, Autti and colleagues rotated a helium-3-filled nafen sample around an axis parallel to the strands in the aerogel [5]. This generated vortices, but the team could not directly measure the circulation around the vortices to check if it corresponded to a half unit. Instead, the researchers relied on a magnetic signal coming from the nuclear magnetism of superfluid helium-3. The interaction between the nuclear magnetic moments of the helium atoms that comprise Cooper pairs is sensitive to the relative orientation of the spin quantization axis and the orbital axis of the molecular pairs. This orientation dependence led to the original identification of the superfluid phases of unconfined helium-3 [8] and to the development of nuclear magnetic resonance (NMR) spectroscopy as a powerful tool for probing the spin and orbital wave function of Cooper-pair condensates in confined geometries [6, 9].

For their detection scheme, the research team first created HQVs under equilibrium conditions with the magnetic field aligned along the rotation axis. Each HQV pairs up with another HQV having an opposite spin current [10]. The spin structure of these pairs becomes detectable when the researchers rotate the magnetic field perpendicular to the rotation axis [10]. The resulting orientation of the spin quantization axis, $\vec{d}$ , between HQV pairs is characterized by a solitary wave, or “soliton,” which is detected as a peak in the NMR spectrum. This peak, which is the unique fingerprint of HQV pairs, occurs at a frequency below the Larmor frequency, $𝛾 B$ , where $𝛾$ is the gyromagnetic ratio for the helium-3 nucleus and $B$ is the magnetic field strength.

The discovery of HQVs in superfluid helium-3 is part of a larger trend of using topology in condensed-matter systems as an organizing principle for understanding quantum states of matter. Recent developments in nanofabrication and nanostructured materials, combined with low-temperature research on quantum fluids, have led to the prediction and discovery of new topological phases of matter and have opened up new research directions in confined and engineered quantum matter. Superfluid HQVs, as well as the polar phase in which they were found, previously existed only on paper and in the minds of a few theoretical physicists. Indeed the existence, stability, and means to create HQVs in superfluid helium-3, combined with experimental tools to manipulate these topological excitations, will likely open new directions for the study of related classes of topological structures in quantum fluids, and possibly stimulate search and discovery in a broad range of condensed-matter systems.

This research is published in Physical Review Letters.

References

L. Onsager, “Statistical Hydrodynamics,” Il Nuovo Cimento 6, 279 (1949).
P. J. Hakonen, O. T. Ikkala, and S. T. Islander, “Experiments on Vortices in Rotating Superfluid $^{3} He A$ ,” Phys. Rev. Lett. 49, 1258 (1982).
G. E. Volovik and V. P. Mineev, “Line and Point Singularities of Superfluid $^{3} He$ ,” Pis'ma Zh. Eksp. Teor. Fiz. 24, 605 (1976), [Sov. Phys. JETP Lett. 24, 561 (1976)].
S. W. Seo, S. Kang, W. J. Kwon, and Yong-il Shin, “Half-Quantum Vortices in an Antiferromagnetic Spinor Bose-Einstein Condensate,” Phys. Rev. Lett. 115, 051301 (2015); J. Jang, D. G. Ferguson, V. Vakaryuk, R. Budakian, S. B. Chung, P. M. Goldbart, and Y. Maeno, “Observation of Half-Height Magnetization Steps in ${Sr}_{2} {RuO}_{4}$ ,” Science 331, 186 (2011).
S. Autti, V. V. Dmitriev, J. T. Mäkinen, A. A. Soldatov, G. E. Volovik, A. N. Yudin, V. V. Zavjalov, and V. B. Eltsov, “Observation of Half-Quantum Vortices in Topological Superfluid $^{3} He$ ,” Phys. Rev. Lett. 117, 255301 (2016).
V. V. Dmitriev, A. A. Senin, A. A. Soldatov, and A. N. Yudin, “Polar Phase of Superfluid $^{3} He$ in Anisotropic Aerogel,” Phys. Rev. Lett. 115, 165304 (2015).
K. Aoyama and R. Ikeda, “Pairing States of Superfluid $^{3} He$ in Uniaxially Anisotropic Aerogel,” Phys. Rev. B 73, 060504 (2006).
A. J. Leggett, “Microscopic Theory of NMR in an Anisotropic Superfluid ( $^{3} He A$ ),” Phys. Rev. Lett. 31, 352 (1973).
J. Pollanen, J. I. A. Li, C. A. Collett, W. J. Gannon, W. P. Halperin, and J. A. Sauls, “New Chiral Phases of Superfluid $^{3} He$ Stabilized by Anisotropic Silica Aerogel,” Nature Phys. 8, 317 (2012).
V. P. Mineev, “Half-Quantum Vortices in Polar Phase of Superfluid $^{3} He$ ,” J. Low Temp. Phys. 177, 48 (2014); “NMR Properties of the Polar Phase of Superfluid $^{3} He$ in Anisotropic Aerogel Under Rotation,” 184, 1007 (2016).

About the Author

James Sauls is Professor of Physics at Northwestern University. He received his Ph.D. in theoretical physics from the State University of New York at Stony Brook, was a postdoctoral fellow at the Nordic Institute for Theoretical Physics in Copenhagen, assistant professor at Princeton University, and held visiting research and faculty appointments at the CNRS and Joseph Fourier University in Grenoble. His research interests are in theoretical physics, quantum fluids and superconductivity, phase transitions, and matter under extreme conditions. Honors include the John Bardeen Prize in superconductivity, the Max Planck Research Prize in Theoretical Physics from the Max Planck Society and Alexander von Humboldt Foundation, and Fellow of the American Physical Society.