Neutrinos Have Mass
Neutrinos dart through matter and space at a pace indistinguishable from the speed of light, so they were initially thought to be massless. And although there have been indications from experiments for many years that these neutral particles actually have a small mass, there has been no definitive proof. But evidence reported in the 24 August PRL has convinced many that atmospherically produced neutrinos oscillate–switch from one variety to another–which would imply that neutrinos indeed have mass. This small mass would require an extension to the Standard Model of particle physics and may provide a window on the remote grand unification scale where the forces of nature become one.
If the three “flavors” of neutrinos–electron, muon, and tau–have mass, it is possible that these flavor states are composed of combinations of their corresponding mass states. Although a neutrino would be produced with a specific flavor, its quantum state would evolve into a combination of the three flavors, with the proportions oscillating in time. The probability of detection as a muon neutrino, for example, would depend on the size of the muon neutrino component at the moment of detection. The smaller the mass difference between the flavors, the longer the oscillation period, so that oscillations would not occur if all of the flavors were equal in mass or were massless (the effect depends only on the difference in mass-squared). The oscillation period also increases with neutrino energy.
Experimental hints that neutrinos might oscillate in this way have been trickling in for decades, mostly from the deficit of electron neutrinos coming from the sun. But in a completely separate phenomenon, there have also been hints of oscillations of muon neutrinos produced in the upper atmosphere. When a cosmic ray proton hits the atmosphere, it produces pions which then decay into muons and muon neutrinos. Each muon decays into an electron, electron neutrino, and another muon neutrino. This decay chain yields two muon neutrinos for every electron neutrino. However, early experiments in the mid-1980s by the Kamiokande detector in the Mozumi mine, Japan, and the Irvine-Michigan-Brookhaven detector near Cleveland suggested that the ratio of muon to electron neutrinos was about one, not two. Those results suggested that half of the muon neutrinos were missing, but proof was needed to show that the cause was neutrino oscillation.
In pursuit of that question, the enormous cylindrical tank of the Super-Kamiokande detector (the successor to Kamiokande) was built. Filled with 50,000 tons of water and insulated from the zoo of cosmic rays by a kilometer of rock above it, “Super-K” searches for ethereal neutrinos with its eleven thousand phototube eyes. Muon neutrinos produce muons that generate a telltale signature of Cerenkov light, a pattern distinguishable from that of electrons spawned by electron neutrinos. After accumulating 535 days of data, the Japanese and American Super-Kamiokande team verified that the ratio of muon neutrinos to electron neutrinos is half the theoretical prediction.
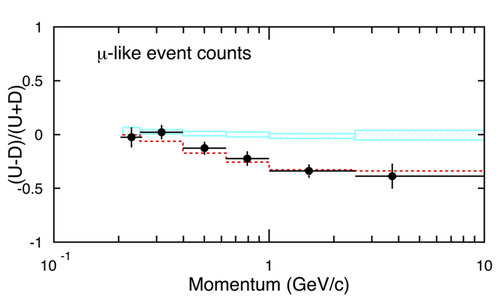
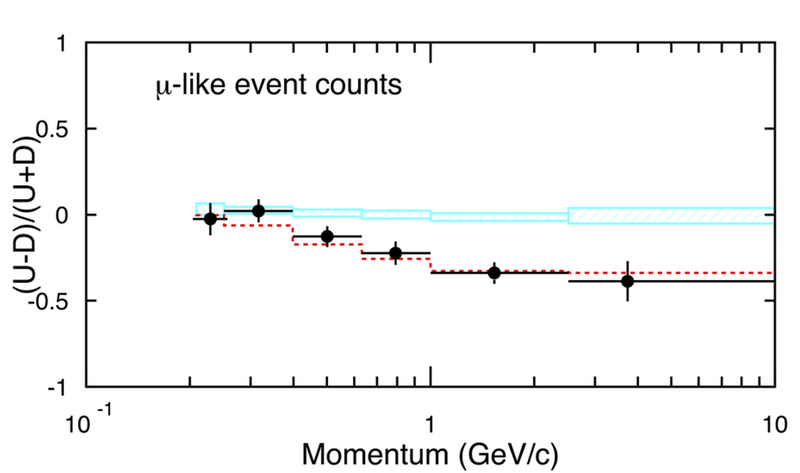
To see if neutrino oscillations explain the observation, the group measured the difference between the number of neutrinos that come down from the atmosphere above, and those which come up through the detector after being produced on the other side of the neutrino-transparent Earth. If neutrinos oscillate, the downward-going ones at higher energies would not have time to oscillate before reaching the detector, whereas energetic neutrinos coming up through the Earth would oscillate several times during their journey. For lower energy neutrinos, the oscillations would occur over much shorter distances, and the oscillation probability would be the same for neutrinos from both directions.
Super-Kamiokande was able to observe this energy-dependent, up-down asymmetry because of its ability to detect high energy muons. The team saw no such asymmetry in the electron neutrinos. The authors conclude that muon neutrinos produced in the atmosphere oscillate into either tau neutrinos or some new neutrino species–in either case, particles that are invisible to Super-K. They further conclude that the mass-squared differences between the oscillating states is between 5×10-4 and 6×10-3eV2. Assuming this result withstands future tests, it will require an extension of the Standard Model of particle physics–not necessarily a difficult task, but it may provide important clues to a more fundamental theory. (Implications for the Standard Model and cosmology.)
In the next decade, a new class of “long baseline” experiments will use controllable neutrino sources from major particle accelerators aimed at far away detectors to study neutrino oscillations directly. Also, the Sudbury Neutrino Observatory in Canada will begin operation in the next year or two, and researchers hope it will tell them more about neutrino properties.
Neutrino physicists respond to these results.
–Robert Garisto
Robert Garisto is the Chief Editor of Physical Review Letters.
More Information
Phys. Rev. Lett. 81, 1774 (31 August 1998, LSND collaboration at Los Alamos)
Phys. Rev. Lett. 81, 2016 (7 September 1998, Kamiokande)