Simplifying Crumpled Paper
The ridges and valleys on a crumpled piece of paper look complex. But there may be only two basic types of formations, which can be stitched together to make up the whole structure, according to the 18 February Physical Review Letters. A team of theorists modeled ripples on a thin sheet and found that a combination of sharp creases and gentle hills and valleys can solve the notoriously difficult equations that describe such sheets. Combining these two building blocks could help researchers study waves on biological cell membranes or the formation of scars on skin.
Robert Schroll of the University of Massachusetts in Amherst noticed that his shower curtain had numerous small ripples along the top, where it was constrained by curtain rings, but that it transitioned to a longer-wavelength ripple along the bottom. He realized that what determined the shape of the curtain over that transition was similar to another problem he was working on, so he and his colleagues built a theoretical model. But “we wouldn’t do all of this work just to explain a shower curtain,” he says. Thin sheets have a lot of industrial applications, such as creating masks for use in lithography or studying the stability of a submarine’s walls, and cell membranes act somewhat like thin sheets as well.
The equations that govern the behavior of thin sheets, the Foppl-von Karman (FvK) equations, are nearly impossible to solve exactly for any but the simplest systems. However, physicists have previously described two characteristic behaviors of thin sheets. The first, called stress focusing, occurs when the elastic energy associated with the deformation of the sheet is focused into point-like peaks (vertices) or creases (lines). The second, called diffuse stress, occurs when the energy is spread smoothly throughout hills or valleys, without the formation of creases. Each of these simpler situations has a known solution for the FvK equations, but they have never been seen together in the same system. Schroll says he doesn’t know for sure that these are the only two types of regions, but “if I had to bet, I’d place money on there only being the two we’ve found.”
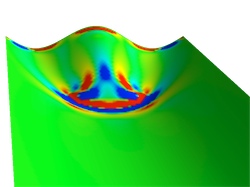
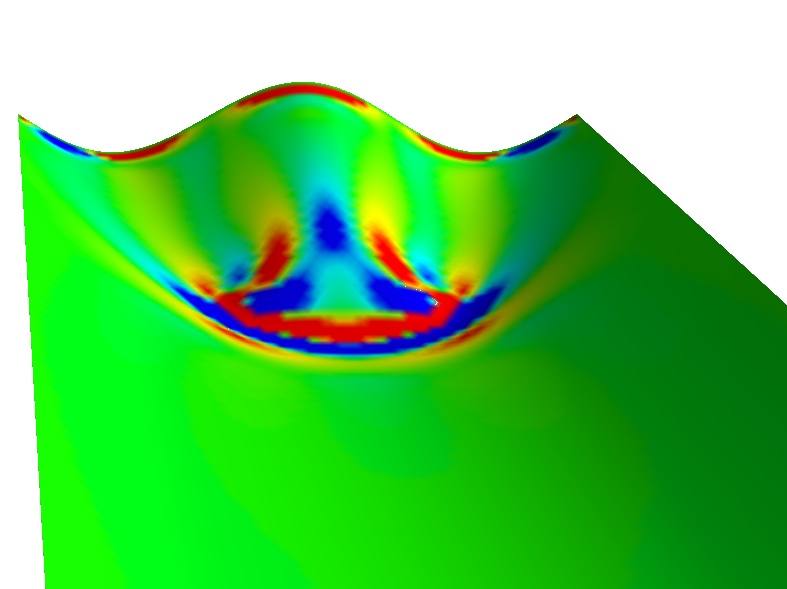
To create a complex topography, Schroll and his colleagues solved the FvK equations for a horizontal sheet of paper configured somewhat like the shower curtain. Their virtual paper had one edge pushed toward the other a bit, so that it bowed outward. They allowed the natural bowing along a perpendicular edge but required the edge opposite the bowed one to have two valleys with a hill in between. The sheet had to smoothly merge these two different edge shapes.
The calculations showed that as you move from the short-wavelength edge toward the long-wavelength edge, the central hill reduces in height and eventually disappears, as would be expected. But the researchers found that it ends in a sharp crease (focused stress), despite the otherwise smooth undulations (diffuse stress) all around. And if the short-wavelength edge is allowed to tilt slightly away from the vertical, the diffuse stress region disappears–instead of a smooth decay, the hill drops steeply, and the crease moves close to the edge.
These results show that both focused stress and diffuse stress can co-exist in the same sheet, the team says, and these two basic solutions of the FvK equations can be stitched together to describe more complex behaviors of a sheet. The team conjectures that a focused stress region is the most efficient way for a sheet to relieve the stress of confinement, but the diffuse stress regions are second best, appearing when the geometrical constraints of the sheet prevent the appearance of focused stress regions.
“This work presents a fascinating generalization of a familiar idea,” says Michael Marder of the University of Texas at Austin. We all know that crumpled paper can have sharp corners as well as smoother curves, he says, and the new results show that the two types occur in general and explain when each type of structure is likely to arise.
–David Harris
David Harris is a freelance science writer in Palo Alto, California.
More Information
New Wrinkle on Fighting Crow’s Feet–Focus story on a wrinkling model that applies to the skin of humans or apples