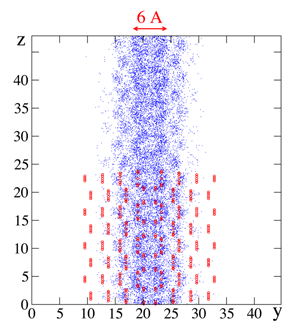
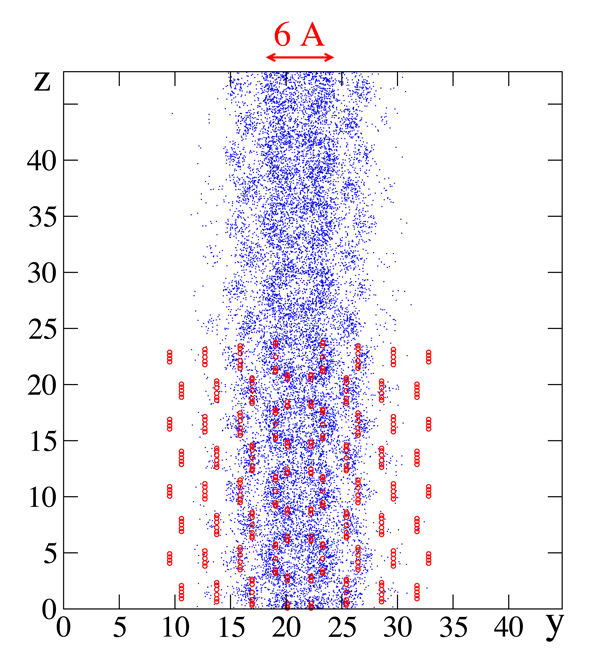
How could a solid be superfluid?

Sébastien Balibar

Viewpoint

How could a solid be superfluid?

Laboratoire de Physique Statistique de l'Ecole Normale Supérieure, associé aux Universités Paris 6 et Paris 7 et au CNRS, 24 rue Lhomond 75005 Paris, France

August 25, 2008• Physics 1, 16

Experiments indicate that, as in a superfluid, mass can flow through solid helium-4 without viscous resistance. Recent calculations shed light on how this may happen thanks to defects in the crystal lattice.

Trent L. Schindler / National Science Foundation.

Video 1: Animation showing the behavior of helium-4 atoms in the Kim and Chan experiments [3, 4]. A cylindrical box is filled with solid helium-4 and suspended from a rod (not shown). The disk rotates back and forth as a torsional oscillator. Clicking on the image begins the animation showing the effects of superfluidity on torsional oscillation [5].

Is it really possible that mass flows without viscous dissipation through a quantum solid? In other words, could a solid be “supersolid”—that is, a superfluid and a solid at the same time? Some experiments suggest so. No one really understands this paradoxical phenomenon yet [1], but a group of six theorists has given us some insight on how this may happen. Writing in Physical Review Letters, L. Pollet and M. Troyer (ETH), M. Boninsegni (University of Alberta), N. Prokof’ev and B. Svistunov (University of Massachusetts), and A. Kuklov (City University of New York) explain how some types of defects in solid helium-4 support mass superflow [2]. It is now up to the experimental groups to check if they are right.

The story began four years ago, when Eunsong Kim and Moses Chan (Pennsylvania State University) filled a little box with solid helium-4. The box was suspended by a rod with which it made a so-called “torsional oscillator” [3,4] that rotates one way, then the other, as in Video 1 [5]. The oscillator had a resonance at a frequency of about 1 kHz, which depended on the oscillating mass. Below a temperature of order 100 mK they observed that the resonance frequency increased as if some of the mass inside the box had decoupled from the moving walls, and from this they proposed that solid helium was perhaps a “supersolid.”

Although paradoxical, in the 1960s A. F. Andreev and L. M. Lifshitz and other theorists thought that this phenomenon was possible in quantum crystals like helium-4 [6]. Their idea was the following: even in the zero-temperature limit, most of the atoms would be localized at the nodes of a periodic lattice but some of the nodes would be vacant. These vacancies could tunnel very quickly from site to site and be delocalized, which would lower the vacancy energy so much that even the ground state of the crystal would contain a nonzero density of these so-called “zero-point vacancies.” As a consequence, the crystal would be “incommensurate,” which means that the number of atoms would be different from the number of sites of the crystal lattice.

Figure caption — **Figure 1:** Two-dimensional projection of a screw dislocation in a hexagonal crystal of helium, as simulated by Boninsegni *et al*. [10] at a temperature of 0.25 K. This is a projection of a three-dimensional crystal that contains a dislocation along the vertical (z) direction. The density of blue points shows the regions that exhibit superfluidity inside the dislocation core. Red circles show the position of atoms (in the lower half-space only) and the dimensions are in Å. The whole picture is the result of a quantum Monte Carlo simulation performed with a particularly efficient algorithm.

In helium-4, where atoms are Bose particles, the vacancies would also be Bose particles. At low temperature, these vacancies could then form a “Bose-Einstein condensate,” that is, a macroscopic matter wave. A vacancy moving one way being equivalent to an atom moving the other way, superfluid mass transport would be possible through this surprising crystal. But at the same time, the crystal would show solid properties due to its localized atoms: it would react elastically to a shear stress; it would be both elastic and superfluid!

This idea is interesting but it could not apply to helium: solid helium-4 is commensurate because the energy of vacancies is not zero but rather on the order of 10 K, so that at 100 mK, the probability of finding a vacancy is of order $e^{- 100}$ , which is totally negligible. Moreover, most physicists in this field agree that a commensurate crystal cannot be supersolid [7]. So what is happening in these helium crystals? The experiments by Kim and Chan have been repeated by several groups working at Cornell, Keio University (Tokyo), and others. But successive experiments have shown that, if it really exists, supersolidity is related to disorder in the solid samples [8,9]. This disorder could be dislocations, grain boundaries, or ill-crystallized regions, which could be liquid or even glassy.

As a result of these experimental developments, predictions were made in 2007 by the aforementioned theorists [10,11]. As shown in Fig. 1, they found that the region inside screw dislocations is superfluid [10] and predicted that helium inside the grain boundaries between crystal grains in polycrystals should also be superfluid [11]. This confirms that such defects may allow superfluidity, but why does it occur? Thanks to the new work by Pollet et al. [2] the underlying physical mechanisms are becoming clear. They find that inside a dislocation or a grain boundary, the local stress is anisotropic and sufficient to bring the vacancy energy to zero, so that the defect is invaded by vacancies that are mobile and superfluid. In a perfect crystal, an invasion by vacancies would lead to melting but inside a dislocation it does not. As a result, Pollet et al. show that solid helium could contain a network of defects, and if these defects are connected to each other, mass could flow from one side of the crystal to the other without friction.

With Pollet’s new results, have we really understood what happens in torsional oscillators? We have clearly progressed, but I don’t think the story is finished. One reason for my doubts is that dislocations are very small objects, about 1 nm in diameter. In order to build a measurable superfluid fraction, one would need an enormous density of dislocations. Some researchers such as Philip Anderson think that there could be a kind of proximity effect, as in superconductors [12]. In this scenario, dislocations are sources of vacancies that may invade the crystal and make it superfluid, but this does not seem to be observed in numerical simulations.

Another difficulty comes from measurements of the shear modulus of helium-4 crystals. Day and Beamish [13] have found that below 100 mK, when the crystals seem to be supersolid, they become stiffer, not softer as one could have expected since mass is supposed to move inside. Furthermore, the way that the elastic shear modulus increases below 100 mK is very similar to the manner in which the frequency of the torsional oscillator increases. The stiffening could be the result of dislocations becoming pinned by isotopic impurities (for example, helium-3 atoms even at very small concentrations). But why would the pinning of dislocations be necessary for supersolidity to appear? As far as I can tell, at the moment nobody knows.

After nearly five years of hard work in several laboratories, helium crystals still appear to be very strange and it is our understanding of the solid state of matter that needs to be reconsidered in depth. I believe that Pollet et al. are on the right track in trying to understand defects in crystals, but the game is far from over. After many years of work on quantum crystals, the understanding of quantum defects has only just started. Of particular interest would be experiments on single defects or on solid samples with well-characterized disorder.

References

Sébastien Balibar and Frédéric Caupin, J. Phys. Condens. Matter 20, 173201 (2008)
L. Pollet, M. Boninsegni, A. B. Kuklov, N. V. Prokof’ev, B. V. Svistunov, and M. Troyer, Phys. Rev. Lett. 101, 097202 (2008)
E. Kim and M. H. W. Chan, Nature 427, 225 (2004)
E. Kim and M. H. W. Chan, Science 305, 1941 (2004)
http://www.nsf.gov/news/news_images.jsp?cntn_id=100323&org=LPA
A. F. Andreev and L. M. Lifshitz, Sov. Phys. JETP 29, 1107 (1969)
For a review of these theoretical aspects, see N. Prokof’ev, Adv. Phys. 56, 381 (2007)
A. S. C. Rittner and J. D. Reppy, Phys. Rev. Lett. 97, 165301 (2006); 98, 175302 (2007); A. S. Rittner and J. Reppy (to be published)
S. Sasaki, R. Ishiguro, F. Caupin, H. J. Maris, S. Balibar, Science 313, 1098 (2006); S. Sasaki, F. Caupin, and S. Balibar, Phys. Rev. Lett. 99, 205302 (2007)
M. Boninsegni, A. B. Kuklov, L. Pollet, N. V. Prokof’ev, B. V. Svistunov, and M. Troyer, Phys. Rev. Lett. 99, 035301 (2007)
L. Pollet, M. Boninsegni, A. B. Kuklov, N. V. Prokof’ev, B. V. Svistunov, and M. Troyer, Phys. Rev. Lett. 98, 135301 (2007)
P. W. Anderson, personal communication (2008)
James Day and John Beamish, Nature 450, 853 (2007)

About the Author

Sébastien Balibar is a CNRS Director of Research working at the Laboratoire de Physique Statistique de l’Ecole Normale Supérieure (ENS), Paris. He received his Ph.D. in 1976 under Albert Libchaber at the ENS and has carried out extensive research in low-temperature and condensed-matter physics. Dr. Balibar was an invited professor at Konstanz Universität, Kyoto University, and Harvard University, where he was a recipient of the Loeb Lectureship. Among various honors, he was elected a fellow of the American Physical Society and shared the Fritz London Memorial Prize in 2005. The author of numerous research papers, he has also written the book La Pomme et l’Atome, (Odile Jacob, Paris, 2005) (The Atom and the Apple: Twelve Tales of Contemporary Physics, Princeton University Press, 2008).