Ultracold neutral plasmas

Plasmas, the most common state of matter in the universe, span an incredible range of parameters, from a density of ${10}^3{\text{cm}}^{-3}$ and temperature of a few hundred kelvin in the aurora of earth’s ionosphere to a density of ${10}^{27}{\text{cm}}^{-3}$ and temperature of ${10}^7$ K in the core of the sun. With the tools of atomic physics and the techniques of laser cooling, we can now create neutral plasmas at temperatures as low as 1K [1]. Having these kinds of laboratory plasmas may help us to better understand the interiors of large planets and white dwarf stars, and allow us to probe new states of matter and unusual liquidlike and crystalline effects in so-called strongly coupled plasmas.

Ultracold plasmas have been created in a number of atomic systems including xenon, rubidium, cesium, strontium, and calcium—essentially any atom that can be easily laser cooled and has a convenient laser wavelength for photoionization. While many plasma experiments tend to require large facilities, ultracold plasmas experiments look much more like atomic physics experiments—tabletop physics with a small vacuum chamber and associated laser hardware—and in fact have been carried out in atomic physics research groups. Because of the rather delicate nature of these plasmas (they exist at low temperature, they only contain ${10}^5$– ${10}^6$ ions, and the experiments are carried out in vacuum), most traditional probes of plasma physics properties are too invasive (for example, electrodes placed in the middle of the plasma). Instead, ultracold plasma researchers measure the electrons or ions leaving the plasma, both spontaneously and extracted, or use laser spectroscopy and imaging for ions with optically convenient transitions.

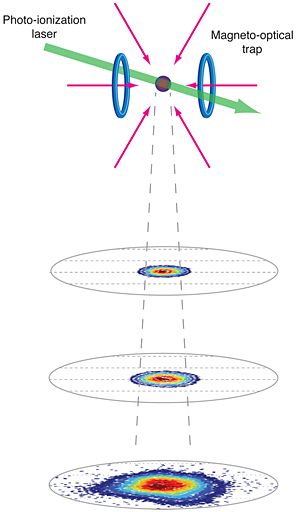
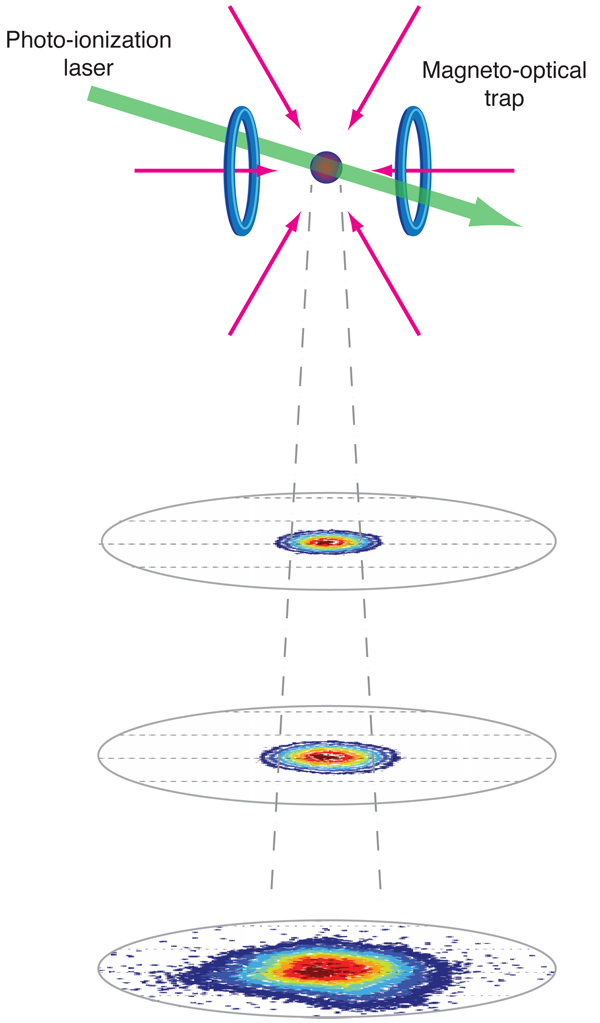
Ultracold neutral plasmas were first observed in 1999 by my research group [2] in an experiment at NIST in which we photoionized a sample of xenon atoms that were laser cooled to a starting temperature of $\sim 10\mu \text{K}$ (Fig. 1). Because the atoms had virtually no thermal energy, the energy available to the plasma was just the excess of the ionizing photon above the ionization limit. This method for creating the plasma releases the electron from the atom as gently as possible. All the subsequent experiments in ultracold plasmas follow this same prescription—reduce the thermal energy of the neutral atoms with laser cooling, and then photoionize near the ionization limit.

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

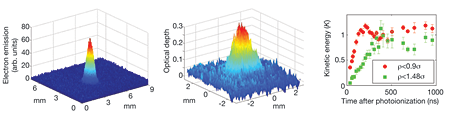
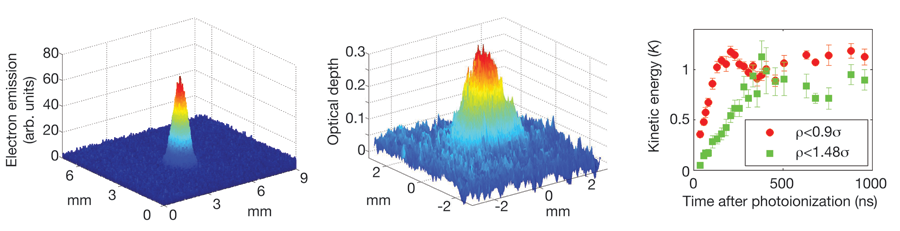
The actual plasma formation can be understood with a simple model. While the neutral atoms are ionized by a laser pulse (which is usually about 10 ns in duration), some of the electrons escape the millimeter-sized cloud (left and center panels of Fig. 2): even at 1 K, an electron has a thermal velocity of 4 km/s. The remaining cloud is slightly positively charged, which forms an attractive Coulomb potential for the next electrons trying to escape. As more electrons leave, the potential well continues to deepen. Once the well depth equals the electron kinetic energy, no more electrons can escape, and a plasma is formed. For typical parameters only a few percent of the electrons need leave, so the overall plasma is almost neutral, and the highly mobile electrons tend to cancel the fields created by the ions, making the system very neutral except on the periphery. The confined electrons exert an outward pressure on the ions, resulting in a plasma expansion into vacuum with a velocity of order 100 m/s (that is, the velocity $v\sim k_B{T}_e/m_i$ , where $k_B$ is Boltzmann’s constant, $T_e$ is the electron temperature, and $m_i$ is the ion mass) and a plasma lifetime of $50-200\mu \text{s}$.

Left image adapted from [23]; right and center images courtesy T. C. Killian, Rice University.

Left image adapted from [23]; right and center images courtesy T. C. Killian, Rice University.

×

The electron and ion temperatures of ultracold plasmas has been an area of continuing interest. One of the original motivations for pushing plasmas to lower temperatures is to access the parameter regime known as strong coupling, where the ratio of Coulomb potential energy to kinetic energy, ${\mathrm{\Gamma }}_{e,i}=e^2/4\pi {ϵ}_{0}a{k}_B{T}_{e,i}$ (where $e$ is the electron charge, ${ϵ}_0$ is the vacuum permittivity, and $a$ is the Wigner-Seitz radius, that is, the average interparticle spacing) is greater than one. Although single-component strongly coupled plasmas have been well studied (laser-cooled ions in Penning traps, and dusty plasmas, for example [3]), strongly coupled neutral plasmas are very difficult to create in the lab, although they do presumably exist in nature at the center of Jovian-type planets and white dwarf stars, for example. As $\mathrm{\Gamma }$ increases above 1, correlations become important as the Coulomb attraction and repulsion starts to dominate thermal motion. Such strongly coupled plasmas should exhibit liquidlike behavior for $\mathrm{\Gamma }\sim 10$ and form crystalline phases for $\mathrm{\Gamma }>200$. If we naively use the initial conditions at ionization, such as a density of ${10}^{10}{\text{cm}}^{-3}$, electron energy (or temperature) of 1 K, and an ion temperature of 1 mK, we would find ${\mathrm{\Gamma }}_e\sim 6$ and ${\mathrm{\Gamma }}_i\sim 6000$, well into the strong-coupling regime.

Nature does not make it easy to form such systems. Researchers in the group of Thomas Killian at Rice University observed [4] a predicted heating effect [5] (disorder-induced heating) that immediately raises the temperatures of both electrons and ions to up to as much as 10 K (depending on density). This can be easily understood: the atomic sample has randomly distributed atoms, and when ionized, the electrons and ions will find themselves sitting in a random Coulomb potential landscape. About half of the particles will be sitting on hilltops, and will quickly roll down converting this potential energy into thermal energy. Another viewpoint is that for a given $\mathrm{\Gamma }$, there is a particular lowest energy state with the appropriate particle position correlations (for instance, a crystalline state), which the state formed by photoionization lacks. The ion and electron temperatures in ultracold plasmas are only weakly connected, because the kinematics of a collision between a very light particle (electron) and a heavy particle (ion) make for very slow energy transfer. Measurements of the ion temperatures (by observing the Doppler shift of the absorption spectrum of laser-excited ions) soon after ionization do suggest the beginnings of strong coupling (measured $\mathrm{\Gamma }$ of ~3–4) and most tellingly observe temporal oscillations in the ion kinetic energy [6], which can only be due to the effects of correlations (right panel of Fig. 2).

The manner in which these plasmas evolve and expand is unusual. The first measurements [7] of ultracold plasma expansion found that above an initial electron $\text{energy}/k_B$ of 10 K, the plasma expanded in accordance with a simple hydrodynamic electron pressure model, but for low energies there was an excess expansion velocity. This was quickly traced down to the effects of collisions in the plasma, in particular three-body recombination, where two electrons and an ion collide to form a highly excited entity called a Rydberg atom (observed using field ionization techniques [8]). The impact on the expansion arises from energy conservation in such a collision, as the extra electron increases its energy by the binding energy of the Rydberg atom. Three-body recombination is a source of heating. This particular collision channel is of such prominence because it scales as $T_{\text{e}}^{-9/2}$ and completely dominates all other mechanisms in ultracold plasmas. Since there are two electrons involved in the collision, the collision rate also scales as the square of the electron density, $\sim n_e^2$, and might be expected to rapidly drop off as the plasma expands ( $n_e$ typically drops by four orders of magnitude during the lifetime of the plasma). But we have to consider what has happened to the electrons during expansion—they are doing work on the ions through electron pressure and thus should be adiabatically cooling (this by itself would predict five orders of magnitude of cooling during the plasma lifetime). So we are left with a competition between strong cooling and a heating process that rapidly turns on as the temperature falls, and an uncertain evolution of the electron temperature and coupling parameter.

Actually obtaining such temperature measurements in ultracold plasmas has turned out to be quite challenging. Although there were a few measurements of electron temperatures that showed the importance of three-body recombination, they tended to only be applicable at early times in the plasma and had large uncertainties. A recent experiment in our lab [9] has exploited the strong temperature dependence of three-body recombination and uses the production rate of Rydberg atoms as a way to measure the temperature. The key to accurately measuring rates was to switch to microwave ionization of the extremely fragile Rydberg atoms and then counting the numbers of neutral Rydberg atoms that reappear. Although the electric field strengths are similar to DC field ionization, their rapid oscillation (at 2.5 GHz) just makes the electrons quiver slightly rather than ripping them out of the plasma. If the microwaves are applied for a short enough time ( $<1\mu \text{s}$) the only effect on the plasma is minimal heating. We found that the measured electron temperatures fall below 1 K at $60\mu \text{s}$, by far the lowest electron temperatures ever observed in a neutral plasma. A new treatment [10] of low energy transfer collisions has recently been proposed that modifies three-body recombination rates and is in agreement with the microwave ionization results. Recently, Bergeson and Robicheaux [11] observed the fluorescence associated with Rydberg atoms cascading to the ground state. The results are in some disagreement with a standard recombination model, suggesting either that the high energy tail of the electrons distribution or large energy transfer electron–Rydberg collisions are not properly treated in such a model, so our understanding of the basic process of recombination is still incomplete.

Although ultracold plasmas can generate large numbers of Rydberg atoms, it was also observed in the beginning of ultracold plasma research that if the ionizing laser was tuned below the ionization limit, forming a cloud of cold Rydberg atoms, it would spontaneously ionize into an ultracold plasma. After a number of mechanisms were proposed, recent research by Li et al. at the University of Virginia [12] has shown the importance of Penning ionization of a pair of Rydberg atoms, a process in which one atom is ionized while the other drops to the ground state. The important discovery was that atom pairs could be excited onto attractive Rydberg–Rydberg potentials, and drawn into the close range necessary for ionization by attractive van der Waals forces, which scale as the 11th power of the principal quantum number n. One motivation for this work is the use of cold Rydberg atoms for quantum information processing, and spontaneous ionization is definitely a bad thing in this case, so it has to be understood and prevented. At higher densities, simple two-body physics may no longer tell the full story, and ionization may be proceeding through many-body absorption of photons [13]. This work highlights the almost smooth transition between highly excited atoms sitting in a plasma and free electrons bound in a plasma. In fact, for typical parameters, the binding energy of an electron in an ultracold plasma is about the same as an $n=80$ Rydberg atom. As a result, identifying which is the plasma electron and which is an atomic electron can be challenging.

Recombination in ultracold plasmas is of great interest in the formation of antihydrogen. There are currently two experiments (ATRAP [14] and ALPHA [15]) operating at CERN whose ultimate goal is the production of trapped ground state antihydrogen (a bound positron and antiproton). Both experiments have observed the production of antihydrogen atoms when they merge cold positron and antiproton plasmas. The plasma densities and temperatures are similar to ultracold plasma parameters, although the antiparticles are held in traps with magnetic fields on the order of a tesla. The big payoff for antihydrogen experiments will be to make precision spectroscopy measurements of the transitions in antihydrogen compared to hydrogen, which may lead to the most precise tests of the CPT theorem for baryons. No antiparticle has ever had its gravitational mass measured, and antihydrogen is our best shot at such a measurement, which is important given our fundamental inability to connect the theory of gravity with quantum mechanics. For any of these applications, it is critical that the antihydrogen atoms be in a well-defined state, which by default is almost certainly the ground state.

As we have seen in ultracold plasma research, recombination proceeds to highly excited Rydberg states that can have very long radiative lifetimes, such that the atoms may leave the trapping volume before they reach the ground state. The ATRAP experiment has made measurements showing that the antihydrogen atoms they detect are in Rydberg states but showed some unexpected features of a surprising number of deeply bound atoms as well as large antihydrogen velocities [16]. These mysteries have recently been explained by Pohl et al. at Harvard University [17], with numerical simulations of the recombination collision that show some fundamental differences between low field and high field recombination and subsequent electron–Rydberg collisions, explaining the enhancement of deeply bound atoms, and the identification of a charge exchange process between antiprotons and antihydrogen that explains the fast atom production. While the antihydrogen collaborations work on ways to produce slow, ground-state trappable atoms, it may be that ultracold plasma research (done at small scale rather than at an accelerator facility) may learn enough about recombination to generate some new ideas for the antihydrogen efforts.

One notable difference between the antihydrogen work and most ultracold plasma research is the large magnetic field. At tesla fields an electron in a Rydberg atom is more tightly bound to the field than to the ion, and the atoms, known as guiding center atoms, follow trajectories more related to charged particle trajectories in crossed $\mathbf{\text{E}}$ and $\mathbf{\text{B}}$ fields than simple neutral atoms. As we can imagine, a collision between a guiding center atom and electrons may act very differently than at low field. There has been recent work by Choi et al. at the University of Michigan [18] to move ultracold plasma research into the regime of high magnetic fields, but without the complications of antiparticles and particle accelerators. Magnetically trapped and cooled rubidium atoms are photoionized to form a plasma in which they observe confinement of both electrons and ions for several milliseconds, electron cooling, and particle loss due to $\mathbf{\text{E}}\times \mathbf{\text{B}}$ drift motion. This experiment is a reversal of the antihydrogen experiments, where the plasma is first confined and then the neutral antihydrogen magnetically trapped (in the future), but should offer insight and guidance for antihydrogen production in terms of high field effects on recombination, plasma lifetimes, and high field Rydberg atom physics.

Because ultracold plasmas are so cold, it should not require large magnetic fields to confine them [note that the cyclotron (Larmor) radius of a 10 K electron is $70\mu \text{m}$ in a 10 G magnetic field]. We recently examined the radial expansion of an ultracold plasma in a uniform field [19]. In a field-free plasma, the electrons are effectively bound to the massive ions, and thus the two charge species expand together at the ion velocity. In a magnetic field where the electron Larmor radius is less than the size of the plasma, the electrons become “bound” to the field lines, and the ions are confined by the electric field from the electrons, a sort of role reversal. In fields of up to 70 G, the radial expansion velocity reduced by a factor of five to 15 m/s. If the electrons are indeed bound to the field lines, how did the plasma expand at all? It is due to ambipolar diffusion, a well-known phenomena in plasmas with oppositely charged particles. An electron and an ion can momentarily pair up, and drift across field lines acting as if they are neutral. The surprise in this case was the scaling that went as $B^{-1/2}$ rather than the expected $B^{-1}$. This is a result of the dynamically evolving nature of expanding ultracold plasmas, as the density and temperature decreases during expansion. Our future plans include adding a magnetic mirror geometry to try to achieve full 3D confinement and the ability to study the plasmas for longer times, although this will still inevitably be limited by diffusion.

Perhaps the defining characteristic of plasmas is the wide variety of collective phenomena that arise out of the long-range Coulomb interaction between the charged particles. Understanding plasma collective behavior is important to the understanding of plasmas ranging from the earth’s ionosphere, the sun, to galaxies. Control of collective plasma modes is critical in various applications including fluorescent lighting and controlled fusion. The long standing challenge to produce a viable source of fusion energy is really a story of learning how to deal with runaway collective behavior that produce plasma instabilities, sapping the reactor of the necessary density and temperature to sustain a fusion reaction.

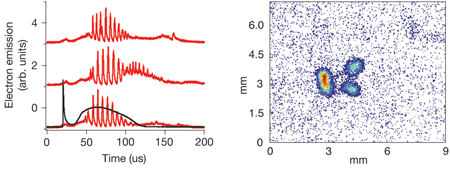
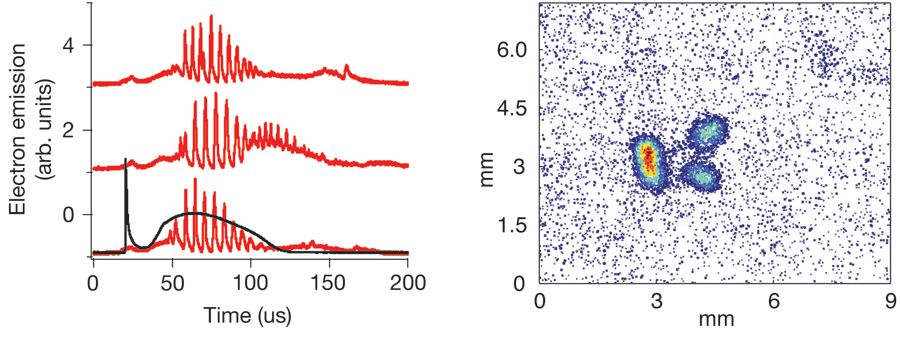
The first observation of a collective mode in an ultracold plasma was the NIST measurement of the plasma (Langmuir) oscillation frequency [7], which is simply the frequency at which electrons oscillate when displaced from the ion centers. Because it depends only on the electron density (and fundamental constants) it was used as a probe of plasma density. More recently, we observed a set of collective modes related to electron sound waves, known as Tonks-Dattner resonances [20]. The first observation of an ultracold plasma instability [21] grew out of attempts to do optical pumping on the neutral atoms. This led us to apply a small ( $\sim 1$ G) magnetic field transverse to the usually present small (~ 10 mV/cm) electric field that guides electrons toward the charged particle detector. The typical ultracold plasma signal, monitoring electrons released from the plasma during its expansion, is a smooth curve of released electrons vs time, due to electrons evaporating out of the Coulomb potential formed by the ions as it gets shallower due to plasma expansion. With the application of the small crossed $\mathbf{\text{E}}$ and $\mathbf{\text{B}}$ fields, periodic emission of pulses of electrons was observed (left panel of Fig. 3). The experiment could produce a plasma once per second, and each shot showed the approximately the same characteristic frequency, albeit with different phase, clearly pointing to plasma instabilities. By varying the applied magnetic and electric fields the frequency of emission was observed to scale linearly with $\mathbf{\text{E}}/\mathbf{\text{B}}$, clearing suggesting a phenomena associated with $\mathbf{\text{E}}\times \mathbf{\text{B}}$ drift velocities. The instabilities occur at surprisingly small fields (10 mV/cm and 0.5 G) and persist with the same frequency over many orders of magnitude change in the expanding plasma density.

×

By measuring the system parameters that lead to possible instabilities as the electrons are magnetized (with collision rate less than Larmor frequency and Larmor radius less than plasma size) and the ions are not, we have identified this phenomenon as a high-frequency drift instability. This has been observed and studied in the context of Hall thrusters, plasma-based spacecraft propulsion engines favored by the Russian space program and which are now under consideration for US spacecraft. Although the parameter regime and mode frequencies agree with this particular instability, there are still some mysteries. The applied magnetic field is perpendicular to the detector axis, so the Larmor motion should prevent the electrons from making it to the detector, unless they undergo large orbits (> 1.5 cm) that take them into a region of high electric field. In an attempt to look for such large orbits, the electron density was imaged by rapidly accelerating the electron cloud onto an imaging charged particle detector. When there are no crossed fields, the electron distribution is a well-behaved Gaussian distribution. With the addition of the transverse field that is associated with the periodic electron emission, the electron distribution is seen to break up into two to three lobes (right panel of Fig. 3). They do not extend to a region to provide escaping electrons, but clearly this large-scale density structure is integral in some way to the instability.

Ultracold plasma physics has grown out of atomic physics technology and research, and it is only natural to try to continue to utilize our techniques to further push the limits of plasma parameters. Experiments with calcium and strontium have the unique feature that there is an easily accessible strong optical transition in the ions. This has been exploited for laser absorption and fluorescence measurements to give images and Doppler spectra of the ions. It is interesting to consider whether we can employ laser cooling of the ions (a well-established atomic physics technology) to generate millikelvin ion temperatures and push the ions very deeply into the regime of strong coupling. Estimates suggest it should be possible , but the challenge will be whether the laser cooling capabilities can win out over the various heating mechanisms that exist in ultracold plasmas, including those that are known and possible others that have not yet been identified. Another intriguing possibility would be to introduce correlations in the neutral atom locations by photoionizing from an optical lattice (a periodic potential for neutral atoms formed by interfering laser beams), although these correlations are likely to be different from the strongly coupled plasma correlations.

Ultracold plasma research is primarily concerned with the fundamental properties of plasma in new parameter regimes, but there is also active ongoing research exploring their use for the production of very monoenergetic electron and ion beams. Research in ultracold plasmas may in the end offer insights into a wide variety of systems, such as plasma propulsion systems, the ionosphere and other astrophysical environments, and inertially confined plasmas for fusion.