Light finds a way through the maze

John Pendry

Viewpoint

Light finds a way through the maze

The Blackett Laboratory, Department of Physics, Imperial College London, London SW7 2AZ, UK

September 15, 2008• Physics 1, 20

Thick layers of disordered materials, such as milk or snow, scatter light so that very little of it gets through. Theorists say that a properly designed combination of incident light waves would be almost completely transmitted and we now have experimental proof of this remarkable result.

Figure caption — **Figure 1:** (Upper left) Light typically scatters strongly from a layer of zinc oxide particles and thus most of the light does not reach the detector. (Upper right) Light that is shaped and phase shifted in an optimum way can pass through the scattering layer so that a large fraction arrives at the detector. The lower left panels show the transmitted intensity distribution of horizontally polarized light in a $15 μ m \times 15 μ m$ square area at the back of the disordered sample. (a) For a nonoptimized incident wavefront. (b) For an optimized wavefront. (Lower right) Intensity summed in the y-direction to average over speckle. Dashed curve (blue), transmission of nonoptimized wavefront; Solid curve (red), transmission of optimized wavefront.

Consider radiation passing through a slab of material. In the absence of disorder, energy flows in an orderly fashion and is distributed among a set of modes or channels defined by the angle of incidence, which remains constant as the light propagates through the slab. Break up the slab into random pieces and the orderly progression of energy is disturbed: the modes are mixed up; lots of energy is scattered back to where it came from and if the disorder is really bad very little energy makes it to the far side of the slab. Now, Ivo Vellekoop and Allard Mosk of the University of Twente report in Physical Review Letters experimental evidence that this scattering may be overcome to allow a large fraction of the incident light to pass through opaque matter [1].

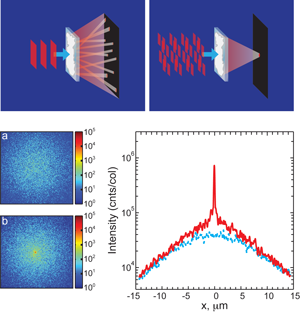
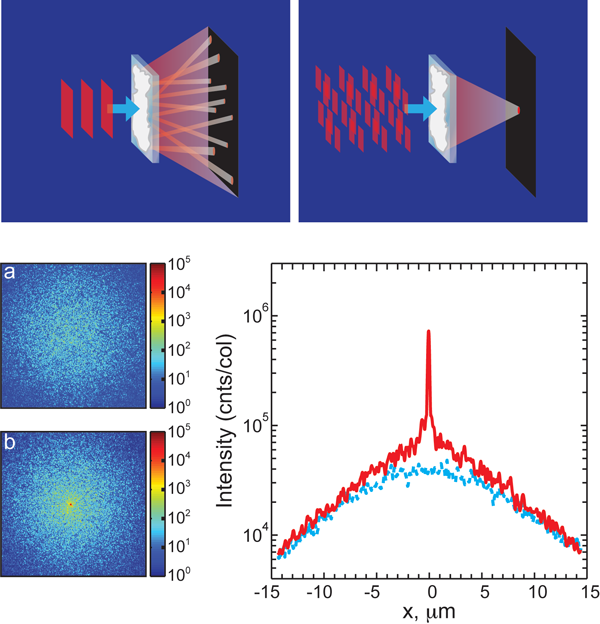
In their experiment they measured how much light is transmitted through a disordered sample. Sure enough, the modes became mixed up and little light emerged. However, they then tried to sneak the light through by sending it at the sample from different angles and with different phases, which were adjusted to optimize transmission of energy (Fig. 1, top panels). Incredibly, transmission could be increased in this way by almost a factor of $10^{3}$ .

In fact, theorists have been predicting this weird effect for some time [2–7]. When transmission channels mix they form new channels. Rather than each of these new channels contributing a little bit to the much-reduced transmission, they divide into two classes: channels that are almost completely closed (i.e., blocking light) and channels that are almost completely open (transmitting light). Hence if an experiment could find the open channels and direct all the incident energy into them, very high transmission should always be possible. Light can always find a way through a maze of disorder. The experiment has been many years in the making, since the first theoretical papers, but now these remarkable conclusions have been confirmed.

The experiment was performed on samples of disordered zinc oxide particles with average diameter of 200 nm, which strongly scatter light so that the mean free path is only $0.85 μ m$ . Two sets of samples were used—one 5.7 and the other $11.3 μ m$ thick. Light from a laser was first reflected off of a liquid-crystal display, which could be contoured to shape the reflected wavefront, and then focussed onto the samples. The liquid-crystal display had 3816 independently programmable segments that were adjusted to optimize transmission. The results of optimization are displayed in Fig. 1 in the lower panels.

Propagation of waves through disordered systems is one of the most challenging topics in theoretical physics. The existence of open and closed channels as discussed above is only one fascinating aspect. Another is the sudden alteration in the nature of the channels as disorder is increased. Weak disorder results in diffusive behavior with which we are all familiar, for example, light scattered by milk. This regime is relatively well understood because it can be treated by perturbation theory [2,4]. At high levels of disorder a phenomenon known as localization sets in and it is much more difficult to find open channels. What happens is that the scattering caused by disorder results in destructive interference of propagating waves, so the light is stopped in its tracks. In fact, the number of open channels falls off exponentially with sample thickness for strong disorder, as opposed to weak disorder where open channels decrease in number inversely with the thickness.

This transition to localization has been endlessly debated in the literature and is still not understood. The normally powerful tool of perturbation theory seems not to work for strong disorder and our understanding remains fragmentary. For this reason the new optical experiments are important. Localization was initially studied in the context of spin diffusion [8] and electron localization, but the additional complication of electron-electron interaction makes experiments hard to interpret. Photons do not normally interact with one another, removing a layer of complexity but still leaving the very challenging and unsolved problem of disorder in its purest form.

Some progress has been made with localized systems, particularly in 1D, where a nonperturbative approach gives a complete solution [9]. Diffusing behavior is never seen in 1D and scattering has always been considered as strong. Nevertheless the open-channel/closed-channel result still holds good and it now has a physical interpretation [10].

In this picture, a 1D optical system might comprise a stack of perfectly flat transparent plates each of a random thickness. At random locations and at random frequencies, resonant traps occur that light finds difficult to enter and difficult to escape from. These form the closed channels—nearly always rejecting the light and preventing it from passing through the system. Just occasionally, in a few samples, the resonances might happen to be uniformly spaced across the sample and lined up in frequency so that incident light can use them as a set of stepping stones, hopping from one resonance to another.

Obviously such an occurrence is quite rare but when it happens transmission can be nearly 100%. These stepping stones or “necklace states,” as they are sometimes called because of their resemblance to a string of pearls, are the dominant contribution to the average transmission through disordered 1D samples. In a box of random 1D samples most will show negligible transmission. Occasionally there will be a sample that has the resonances all lined up and that will show very high transmission. Hence the expression “maximal fluctuations” [10,11].

The necklace states remained a theorists’ pipe dream until recently when two other groups confirmed their existence though experiment. The group of Diederik Wiersma (University of Florence, Italy) constructed optical systems comprising alternate layers of high- and low-refractive-index materials arranged to have random thicknesses [12]. The crucial point in their experiment was that the layers were extremely flat so the light was either transmitted or reflected but never altered its angle to the normal. In this way the system is, in effect, one dimensional. They were able to find samples that showed anomalously high transmission and identified the associated necklace states. More or less simultaneously, Azi Genack’s team (City University of New York) worked at microwave frequencies, filling a waveguide with random elements [13]. They too were able to confirm the presence of necklace states.

In fact, the open-channel/closed-channel result has been shown to be a universal theorem, independent of dimensionality and independent of whether the disorder is strong or weak. For strong disorder, when systems are localized, the 1D picture of transmission through necklaces of resonances strung from one side of the system to the other gives an intuitive understanding. For the 2D and 3D systems the most probable necklaces are the shortest ones and tend to link opposite sides of the sample, giving a more or less direct route across. In contrast, for weak disorder, the open channels have a more complex structure. Rather than as chains of localized resonances, they can be thought of as meandering creeks following a random path between the two sides of the sample. As disorder is increased, more and more of the creeks reach a dead end without crossing the sample and the few remaining connections take a more direct route. At the transition to localization the picture remains unclear and a challenge for theorists like myself. The catalyst for resolution of this issue will be further experiments similar to the ones reported by Vellekoop and Mosk but extended to strongly disordered systems near the localization threshold. Thus the recent optical experiments go directly to the heart of this problem and are like the bugle call of cavalry charging to the rescue of hapless theorists.

References

I. M. Vellekoop and A. P. Mosk, Phys. Rev. Lett. 101, 120601 (2008)
O. Dorokhov, Sol. St. Comm. 51, 381 (1984)
P. D. Kirkman and J. B. Pendry, J. Phys. C 17, 5707 (1984)
Y. Imry, Europhys. Lett. 1, 249 (1986)
P. A. Mello, P. Pereyra, and N. Kumar, Ann. Phys.-New York 181, 290 (1988)
J. B. Pendry, A. Mackinnon, and A. Prêtre, Physica A 168, 400 (1990)
J. B. Pendry, A. MacKinnon, and P. J. Roberts, Proc. Roy. Soc. 437, 67 (1992)
P. W. Anderson, Phys. Rev. 109, 1492 (1958)
J. B. Pendry, Adv. Phys. 43, 461 (1994)
J. B. Pendry, J. Phys. C 20, 733 (1987)
A. V. Tartakovskii, et al., Sov. Phys. Semicond. 21, 370 (1987)
J. Bertolotti, S. Gottardo, D. S. Wiersma, M. Ghulinyan, and L. Pavesi, Phys. Rev. Lett. 94, 113903 (2005)
K. Y. Bliokh, Y. P. Bliokh, V. Freilikher, A. Z. Genack, B. Hu, and P. Sebbah, Phys. Rev. Lett. 97, 243904 (2006)

About the Author

John Pendry obtained his Ph.D. in 1969 from Cambridge University, UK, where, apart from a year spent at AT&T Bell Laboratories, he remained until 1975. There followed six years at the Daresbury Laboratory as head of the theoretical group. Since 1981 he has worked at the Blackett Laboratory, Imperial College London, where he has served as Dean, Head of the Physics Department, and Principal for Physical Sciences. His research interests are broad, originally centering on condensed matter theory but now extending into optics. He has worked extensively on electronic and structural properties of surfaces, transport in disordered systems, and in the past ten years has developed the theory behind metamaterials, negative refraction, and cloaking.(Author photograph: Imperial College London/Mike Finn-Kelcey)