Quantum computing over the rainbow

Jeremy L. O’Brien

Viewpoint

Quantum computing over the rainbow

Centre for Quantum Photonics, H. H. Wills Physics Laboratory & Department of Electrical and Electronic Engineering, University of Bristol, Merchant Venturers Building, Woodland Road, Bristol BS8 1UB, United Kingdom

September 22, 2008• Physics 1, 23

Laser beams made up of millions of sharply defined and coherently locked optical frequencies, called optical frequency combs, may provide a way to implement a powerful quantum computer.

Figure caption — **Figure 1:** (Left) Schematic representation of the frequency comb (OFC) generated in an optical parametric oscillator (OPO), showing modes 1–12 (out of millions). The OPO contains a nonlinear crystal which has been engineered to couple multiple pump and OFC modes simultaneously, such that pumping the OPO at different frequencies (red and green) entangles pairs of modes in the OFC, as indicated. The simple graphs below show how each of the modes is entangled, e.g., 1 is connected to 12 by the green pump, but 12 is connected to 7 by the red pump, which in turn connects back to 6. (Right) A toroidal cluster state, with substructure, encoded in an optical frequency comb and universal for quantum computation. Circled region at left shows four macro-nodes, each of which contains four physical nodes (magnified view at right), showing the extensive amount of entanglement that is possible with optical frequency combs in an optical parameter oscillator

The worldwide quest to build a quantum computer is being fueled by the promise of exponentially greater computational power for particular tasks. The physical form that such a device might take is the subject of hot speculation owing to the extreme difficulty in manipulating and controlling quantum systems. Now, Nicolas C. Menicucci of Princeton University and the University of Queensland, Steven T. Flammia at the Perimeter Institute, and Olivier Pfister of the University of Virginia present in Physical Review Letters [1] a vision for a quantum computer that encodes information in light beams that are massively entangled. They accomplish this using an optical frequency comb, made of millions of classically coherent optical modes. This “top-down” approach to generating a highly entangled cluster state holds great promise for the massive parallelism required for scaling to a useful device.

Quantum information science investigates what additional power and functionality can be realized by harnessing uniquely quantum mechanical effects, such as state superposition (wavelike behavior in quantum mechanics) and entanglement (nonclassical correlations of physically separated systems) [2]. In addition to fundamental physical insights, this program has already resulted in commercial systems that use quantum key distribution to improve communication security [3]. In the future, quantum metrology may enable greater measurement precision [4] and quantum lithography aims to define features smaller than the wavelength of light [5]. But the grand prize is a quantum computer—a device that encodes information in quantum systems and processes that information using the laws of quantum mechanics to realize unprecedented computational power.

Of the various approaches to realizing quantum technologies, photons are an ideal choice for their low-noise and high-speed transmission and have been widely used in quantum communication [3], quantum metrology [6,7], and quantum lithography [8]. The difficulty in all-optical quantum computing has been the need for a massive optical nonlinearity to realize the interaction between photons required for two-qubit logic gates (photons normally ignore each other unless they can interact via a nonlinear medium). This problem was solved with a scheme devised by Knill, Laflamme, and Milburn (KLM) [9], which showed that single-photon measurements could be used to realize the required nonlinearities. Although the KLM scheme required only single-photon sources, detectors, and linear optical elements (beam splitters and phase shifters), a large number of them are required because these measurement-induced nonlinearities are nondeterministic.

This large resource overhead has been dramatically reduced by another development: one-way quantum computing (OWQC) schemes. In the standard quantum circuit formulation of quantum computing, a register of qubits (discrete two-level quantum systems) is initialized, then subjected to a sequence of quantum logic gates that implement the desired algorithm, and then measured, in close analogy with the circuit model for Boolean logic used in conventional computing (regardless of the physical implementation being used). A major departure from this picture is OWQC, where computation proceeds via a sequence of single qubit measurements on a highly entangled cluster state of many qubits [10]. Loosely, one can think of the cluster state as the hardware and the particular sequence of measurements as the software. Each measurement consumes some of the cluster state and since quantum measurements are fundamentally irreversible, the process is “one way.”

Somewhat surprisingly, optical implementations of OWQC were proposed and shown to dramatically reduce the worrisome resource overhead of KLM [11–13], as well as promising favorable fault tolerance thresholds (the error rate tolerable in a full-scale device) [14,15]. Along with experimental demonstrations [16], these new schemes have seen the optical approach to quantum computing grow in stature to become a leading contender [17]. However, the task of controlling the interactions between individual photons to build the required cluster state remains daunting.

In both quantum circuit and one-way formulations, information is typically encoded in two-dimensional qubits, although higher dimensional systems have been considered (e.g., [18]). Encoding in continuous variable (CV) systems (as opposed to discrete systems, such as two-level qubits) was motivated by the fact that many of the key steps in quantum information protocols could be efficiently realized [19–21]. In particular, encoding in the amplitude and phase of a light field enables important operations to be implemented deterministically with linear optics, in contrast to the single photon case. This is because the type of detection used is interference detection of the fields, which has almost perfect quantum efficiency.

Recently, Menicucci and colleagues showed that OWQC could be extended to the CV regime [22], and proposed an optical implementation relying on “squeezing,” where the uncertainty (or noise) in one variable is reduced at the expense of the uncertainty in another (conjugate) variable, bounded by the Heisenberg uncertainty principle: $Δ x Δ p \geq ħ / 2$ , where $Δ x$ and $Δ p$ are the two conjugate variables. This process requires nonlinear optical crystals to perform the squeezing—which is less demanding than in the single photon case and able to operate deterministically. Continuous variable one-way computing was dramatically simplified in a scheme that reduced the requirements for crystals to do the squeezing, and also addressed finite squeezing errors [23], inspiring an experimental demonstration of a four-mode cluster state [24,25]. However, the problem remained that these schemes built the cluster state in a “bottom-up” fashion, adding one qumode (the CV analogue of a qubit) at a time, thereby leading to the need for a complex multipath optical system.

A significant breakthrough, in terms of practical implementations, came with the realization that a single optical parametric oscillator (OPO)—a nonlinear crystal that fuses or splits photons, sandwiched between the two mirrors of an optical cavity—could be used to directly generate cluster states by pumping it with several laser frequencies simultaneously, thereby removing the need for the complex multipath optics. Now Menicucci, Flammia, and Pfister [1] have shown that a CV cluster state suitable for universal quantum computing can be efficiently generated in the quantum version of an optical frequency comb generated in a single OPO.

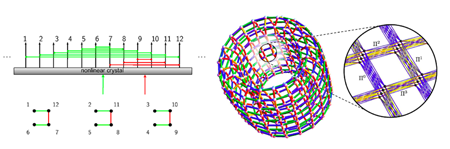
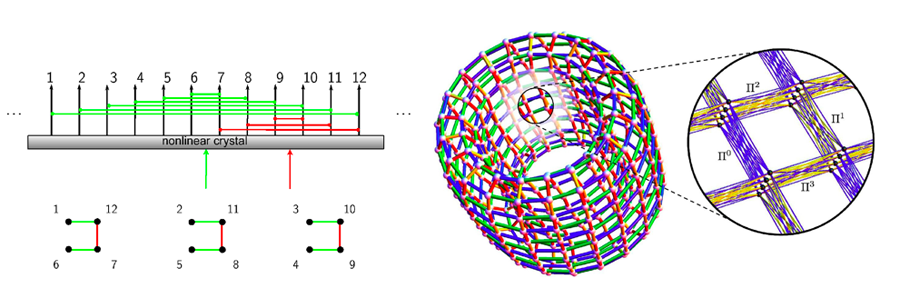
The spectrum (Fig. 1, left ) of an optical cavity consisting of two facing mirrors is made up of equally spaced resonant frequencies—an optical frequency comb (OFC), consisting of millions of modes with coherence properties that have found spectacular application in time and frequency metrology, as highlighted by the 2005 Nobel Prize [26]. Each resonant frequency mode behaves like a quantum harmonic oscillator and can be considered a CV qumode. An OPO is formed when a nonlinear optical material is inserted into such an optical cavity. An OPO enables the absorption of a pump photon at frequency $ω_{p}$ (supplied by an external laser) and simultaneous creation of two daughter photons at OFC frequencies $ω_{m}$ and $ω_{n}$ , where $ω_{p} = ω_{m} + ω_{n}$ , as well as the reverse process where photons are combined. These interactions result in CV entanglement between the $ω_{m}$ and $ω_{n}$ qumodes of the OFC. By engineering the nonlinear material to enable multiple such interactions, and pumping the OPO with several different frequencies, a highly entangled state can be written onto the OFC .

The authors go on to show that an object called a toroidal supergraph, shown in the right panel of Fig. 1, can be created via such a scheme and is universal for quantum computation. This object shows graphically how the qumodes are entangled with each other. Each “macro-node” in the supergraph (left side of right-hand panel) consists of four physical nodes (right side of panel). Measuring one variable ( $x$ , say) on each physical node in three of the four “layers” leaves the remaining layer in a cluster state that is universal for quantum computing.

This scheme represents a remarkably compact and efficient device for generating massive cluster states for OWQC that overcomes many of the challenges standing before the realization of useful quantum processors. The hardest part of the optical nonlinearity engineering has already been demonstrated [27], and the requirement to truncate the nonlinear interactions, so that exactly the right cluster state is created, looks possible. Controlling quantum states of light on an optical chip has recently been demonstrated [28] and may find promising application to frequency comb schemes. In addition, the issue of finite squeezing and other imperfections must be considered in a full fault tolerance analysis. If these challenges can be met we may see massive entangled states being generated in the blink of an eye. In August this year Olivier Pfister presented exciting experimental progress towards these new ideas at the Conference on Quantum Communication, Measurement and Computing (QCMC) in Calgary—so stay tuned for more.

References

N. C. Menicucci, S. T. Flammia, and O. Pfister, Phys. Rev. Lett. 101, 130501 (2008)
M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information (Cambridge University Press, 2000)[Amazon][WorldCat]
N. Gisin, G. Ribordy, W. Tittel, and H. Zbinden, Rev. Mod. Phys. 74, 145 (2002)
V. Giovannetti, S. Lloyd, and L. Maccone, Science 306, 1330 (2004)
A. N. Boto, P. Kok, D. S. Abrams, S. L. Braunstein, C. P. Williams, and J. P. Dowling, Phys. Rev. Lett. 85, 2733 (2000)
T. Nagata, R. Okamoto, J. L. O'Brien, K. Sasaki, and S. Takeuchi, Science 316, 726 (2007)
B. L. Higgins, D. W. Berry, S. D. Bartlett, H. M. Wiseman, and G. J. Pryde, Nature 450, 393 (2007)
Y Kawabe, H. Fujiwara, R. Okamoto, K. Sasaki, and S. Takeuchi, Opt. Express 15, 14244 (2007)
E. Knill, R. Laflamme, and G. J. Milburn, Nature 409, 46
R. Raussendorf and H. J. Briegel, Phys. Rev. Lett. 86, 5188 (2001)
N. Yoran and B. Reznik, Phys. Rev. Lett. 91, 037903 (2003)
M. A. Nielsen, Phys. Rev. Lett. 93, 040503 (2004)
D. E. Browne and T. Rudolph, Phys. Rev. Lett. 95, 010501 (2005)
C. M. Dawson, H. L. Haselgrove, and M. A. Nielsen, Phys. Rev. A 73, 052306 (2006)
M. Varnava, D. E. Browne, and T. Rudolph, Phys. Rev. Lett. 100, 060502 (2008)
P. Walther, K. J. Resch, T. Rudolph, E. Schenck, H. Weinfurter, V. Vedral, M. Aspelmeyer, and A. Zeilinger, Nature 434, 169 (2005)
J. L. O'Brien, Science 318, 1567 (2007)
J. Joo, P. L. Knight, J. L. O’Brien, and T. Rudolph, Phys. Rev. A 76, 052326 (2007)
S. Lloyd and S. L. Braunstein, Phys. Rev. Lett. 82, 1784 (1999)
S. D. Bartlett, B. C. Sanders, S. L. Braunstein, and K. Nemoto, Phys. Rev. Lett. 88, 097904 (2002)
S. L. Braunstein and P. van Loock, Rev. Mod. Phys. 77, 513 (2005)
N. C. Menicucci, P. van Loock, M. Gu, C. Weedbrook, T. C. Ralph, and M. A. Nielsen, Phys. Rev. Lett. 97, 110501 (2006)
P. van Loock, C. Weedbrook, and M. Gu, Phys. Rev. A 76, 032321 (2007)
M. Yukawa, R. Ukai, P. van Loock, and A. Furusawa, Phys. Rev. A 78, 012301 (2008)
X. Su, A. Tan, X. Jia, J. Zhang, C. Xie, and K. Peng, Phys. Rev. Lett. 98, 070502 (2007)
http://nobelprize.org/nobel_prizes/physics/laureates/2005/
R. C. Pooser and O. Pfister, Opt. Lett. 30, 2635 (2005)
A. Politi, M. J. Cryan, J. G. Rarity, S. Yu, and J. L. O'Brien, Science 320, 646 (2008)

About the Author

Jeremy O’Brien is professor of physics and electrical engineering at the University of Bristol, where he leads the Centre for Quantum Photonics (CQP) (http://www.phy.bris.ac.uk/groups/cqp”>www.phy.bris.ac.uk/groups/cqp). He received his Ph.D. in physics from the University of New South Wales in 2002 for experimental work on correlated and confined electrons in organic conductors, superconductors and semiconductor nanostructures, as well as progress towards the fabrication of phosphorus in a silicon quantum computer. As a research fellow at the University of Queensland (2001–2006) he worked on quantum optics and quantum information science with single photons. CQP’s efforts are focused on the fundamental and applied quantum mechanics at the heart of quantum information science and technology, ranging from prototypes for scalable quantum computing to generalized quantum measurements, quantum control, and quantum metrology.