Reconnecting to superfluid turbulence

Joseph J. Niemela

Viewpoint

Reconnecting to superfluid turbulence

The Abdus Salam International Center for Theoretical Physics, Strada Costiera 11, 34014 Trieste, Italy

October 6, 2008• Physics 1, 26

Images of vortex motion in superfluid helium reveal connections between quantum and classical turbulence and may lead to an understanding of complex flows in both superfluids and ordinary fluids.

Figure caption — **Figure 1:** (Left) A vortex reconnection in which two vortex lines meet, the lines break and then reform by swapping the broken lines. A model employing such reconnections was able to account for turbulence in a superfluid [15]. (Right) These reconnections can create Kelvin waves in which a vortex line oscillates about an equilibrium position like a plucked string (the rightmost wavy vortex compared to the undisturbed filament to its left). These waves, in turn can produce phonons in the superfluid that dissipate turbulent energy.

Superfluid flows are interesting playgrounds, where hydrodynamics confronts quantum mechanics. One of the more important and interesting questions is what a complex turbulent flow would look like in a superfluid that was prevented from rotational motion except for circulation about individual, discrete vortex filaments, each having single quanta of circulation about a core of atomic dimensions. This is a great simplification when compared to ordinary turbulence, in which vortices and eddies can have any strength and size. A number of recent works, which have substituted superfluids for ordinary fluids in standard turbulence experiments, have suggested that turbulence in the two fluids is nearly indistinguishable. However, in a recent paper in Physical Review Letters, M. S. Paoletti, M. E. Fisher, and D. P. Lathrop at the University of Maryland, and K. R. Sreenivasan of the Abdus Salam International Center for Theoretical Physics, Trieste, have probed turbulent superfluid flow at small enough scales to see a clear difference [1]. This was achieved by dressing the quantized vortices in turbulent superfluid liquid $^{4} He$ with small clusters or particles of frozen hydrogen, formed by injecting a small amount of $H_{2}$ diluted with helium gas into the liquid helium, and then optically tracking their motion.

The difference is not only dramatic—strongly non-Gaussian distributions of velocity replacing the near-Gaussian statistics in classical homogeneous and isotropic turbulence—but it appears to also have a simple explanation. Reconnections between quantized vortices occurring at the microscopic level of the core can give rise to the same statistical signature that these authors have observed. Such events, established experimentally here as a robust feature, are necessary to fully explain turbulence in superfluids and fundamental to understanding how a pure superfluid like $^{4} He$ at absolute zero can shed its turbulent energy in the complete absence of viscosity.

The reconnections we have in mind can be roughly described as follows: two vortex filaments that approach each other closely, attempt to cross, forming sharp cusps at the point of closest approach. At this point they can break apart, so that part of one vortex reconnects with part of the other, and so forth, significantly changing topology. Reconnections, which are a significant feature of superfluid turbulence, are not unique to it, and can occur in ordinary fluids [2], magnetized plasmas [3], and perhaps even between cosmic strings [4]. Reconnection between broken magnetic field lines in the sun is a relatively common occurrence leading to solar flares. However, there is a fundamental difference: classical reconnections are related to energy dissipation through viscosity, whereas in quantum fluids they take place due to a quantum stress acting at the scale of the core without changes of total energy [5].

Liquid $^{4} He$ becomes superfluid below about 2.2 K, resulting from a type of Bose condensation as the de Broglie wavelength of the individual helium atoms becomes comparable to the average spacing between them. It then behaves as if it were composed of two intermingling and independent fluids: a superfluid with zero viscosity and zero entropy, and a viscous normal fluid, each having its own velocity field and density, where the ratio of superfluid to normal fluid density varies from 0 at the transition to 1 at absolute zero. From this model it follows that the superfluid component must also be irrotational (the curl of velocity must be zero) and this would have seemed to rule out turbulence altogether were it not for the peculiar vortices that are at the “core” of this story.

These vortices, first proposed by Onsager [6] and Feynman [7], can easily be seen [8] in solutions of the nonlinear Schrödinger equation (NLSE) for the condensate wave function of an ideal Bose gas. For these vortex solutions, a coherence length gives the distance over which the amplitude of the wave function rises radially from zero to some constant value. Since the superfluid density is given by the squared modulus of the wave function, this approximately defines the size of the vortex core, which for superfluid $^{4} He$ is extremely small, on the order of one angstrom. The vortex circulation is obtained by integrating the superfluid velocity around a loop enclosing the superfluid-free core (thus avoiding the irrotational condition of the two fluid model) and the solitary stable value that results, namely Planck’s constant divided by the mass of a single helium atom, yields singly quantized line vortices [9].

M. S. Paoletti et al. [1]

Video 1: individual reconnection events are annotated by white circles and evidenced by groups of hydrogen clusters rapidly separating from one another. The clusters that are trapped on the vortices enable the authors to measure the separation as the vortices approach and retract from one another.

Feynman [7] suggested a model for turbulence in the superfluid, which he envisioned as a tangle of such quantized line vortices. But how could a collection of these vortices, having just one quanta of circulation each, resemble classical turbulence in a viscous fluid with all its swirls from large to small? More specifically, would the statistical properties of a turbulent superfluid match those of classical turbulence? For this, we start with the following picture for ordinary fluids: energy injected into a flow at some large scale is transferred without dissipation by a cascade process to smaller and smaller scales, until it is finally dissipated into heat at the smallest scale where viscosity becomes important.

In the 1940s, a dimensional analysis by Kolmogorov [10] corresponding to this picture of turbulence produced the well-known spectral energy density $E (k) = c ϵ^{2 / 3} k^{- 5 / 3}$ for wave numbers $k$ between those of energy injection and dissipation, where $c$ is a constant and $ϵ$ the energy dissipation rate per unit mass. This spectral distribution should be independent of how the turbulence was generated in the first place. With this as background, Maurer and Tabeling [11] showed that for the turbulent flow between two counter-rotating discs, the same Kolmogorov energy spectrum with wave-number exponent -5/3 could be observed above and below the transition temperature in liquid $^{4} He$ . Similar experiments with moving grids [12] also showed this quantum mimicry of classical turbulence. What is going on here?

These experiments had at least two things in common: the fraction of normal nonsuperfluid was small but not negligible, and the measurements were sensitive to scales much larger than that of individual vortex lines in the turbulent state. About the first, note that motion of a quantized vortex relative to the normal fluid produces a mutual friction force [13], coupling the two fluids at large scales (as well as providing dissipation at small ones), so it is not unthinkable then that both normal and superfluid act together to produce a Kolmogorov spectrum. This may take place [14] as a result of a partial or complete polarization, or local alignment of spin axes, of a large number of vortex filaments that mimics the range of eddies we see in classical flows. A simple example of such polarization under nonturbulent conditions is the well-known mimicking of solid body rotation in a rapidly rotating container filled with superfluid helium, which results from the alignment of a large array of quantized vortices all along the axis of rotation [8].

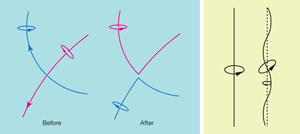
At the scale of individual vortices, Schwarz [15] developed numerical simulations of superfluid turbulence, based on the assumption that vortex filaments approaching each other too closely will reconnect (see the left panel of Fig. 1). Using entirely classical analysis, he was able to account for most of the experimental observations in the commonly studied thermal counterflow, a flow in which the normal fluid carries thermal energy away from a heater and a mass-conserving counter-current of superfluid is produced. Koplik and Levine [8], using the nonlinear Schrödinger equation, showed that Schwarz’ assumptions about reconnections were correct. Even this flow, which unlike the other experiments mentioned above, has no classical analog, also exhibits a classical decay when probed on length scales that are large compared to the average intervortex line spacing [16].

Vortex reconnections should be frequent in superfluid turbulence [17] and this is a fundamental difference from the classical case. At absolute zero, where there is neither viscosity nor mutual friction to dissipate energy, reconnections between vortices are expected [18] to lead to Kelvin waves along the cores (see right panel of Fig. 1), allowing the energy cascade to proceed beyond the level of the intervortex line spacing. Kelvin waves are defined as helical displacements of a rectilinear vortex line propagating along the core. When a vortex reconnection occurs, the cusps or kinks at the crossing point (see above) can relax into Kelvin waves and subsequent reconnections in the turbulent regime generate more waves whose nonlinear interactions lead to a wide spectrum of Kelvin waves extending to high frequencies. At the highest frequencies (wave numbers) these waves can generate phonons, thus dissipating the turbulent kinetic energy. The bridge between classical and quantum regimes of turbulence [19,20], it seems, must be provided by numerous reconnection events.

In the work of Paoletti et al. [1], a thermal counterflow as described above is allowed to decay and then probed at the level of discrete vortex lines by illuminating the hydrogen particles moving with the vortices with a laser light sheet. Viewing the scattered light at right angles to the sheet with a CCD camera allows the motion of the vortices to be tracked (see Video 1). This relies on previous work showing that hydrogen tracers could be trapped on the vortices [21,22]. Large velocities of recoil associated with reconnection events have recently been observed experimentally [23] and in simulations [24]. Paoletti et al. [1] are able to show that the observed, strongly non-Gaussian distributions of velocity due to these atypically large velocities are quantitatively consistent with the frequent reconnection of quantized line vortices. To the extent that turbulent flows are necessarily characterized by their statistical properties, this work provides a clear experimental foundation for a bridge connecting the classical and quantum turbulent regimes.

While insights from the well-studied turbulence problem in ordinary flows have allowed us to move forward in understanding quantum turbulence, the reverse might be said as well: the knowledge we gain there may well yield new insights into classical turbulence, a problem of immense interest in both engineering and large natural flows in fluids and plasmas, and for which a satisfying theoretical framework has yet to be found. Just as in the classical problem, experiments and simulations play a large role, and this leads to many challenges, especially as the temperature is lowered to a pure helium superflow regime. The work of Paoletti et al. [1] is a large step in this direction, allowing us to experimentally confirm our picture of how quantum turbulence proceeds. Going to very low temperatures will require different and more difficult techniques of generating the turbulence than these authors used (in the almost complete absence of the normal component) but ultimately the freely vibrating vortices there may give us the best opportunity to listen clearly to the strange and complex sounds emitted from an “instrument” whose quantum strings are plucked by reconnections.

References

M. S. Paoletti, M. E. Fisher, K. R. Sreenivasan, and D. P. Lathrop, Phys. Rev. Lett. 101, 154501 (2008)
S. Kida, M. Takaoka, and F. Hussain, J. Fluid Mech. 230, 583 (1991)
E. R. Priest and T. G. Forbes, Magnetic Reconnection: MHD Theory and Applications[Amazon][WorldCat] (Cambridge University Press, 2007)
A. Hanany and K. Hashimoto, arXiv:hep-th/0501031v2 (2005)
M. Leadbeater, T. Winiecki, D. C. Samuels, C. F. Barenghi, and C. S. Adams, Phys. Rev. Lett. 86, 1410 (2001); C. F. Barenghi, Physica D 237, 2195 (2008)
R. J. Donnelly, Quantized Vortices in Helium II[Amazon][WorldCat] (Cambridge University Press, 1991)
R. P. Feynman, in Progress in Low Temperature Physics, Vol. 1, edited by C. J. Gorter (North-Holland, Amsterdam, 1955)
J. Koplik and H. Levine, Phys. Rev. Lett. 71, 1375 (1993)
W. F. Vinen, Proc. Roy. Soc. Lond. A Mat. 260, 218 (1961)
A. Kolmogorov, Dokl. Acad. Nauk SSSR 30, 301 (1941)
J. Maurer and P. Tabeling, Europhys. Lett. 43, 29 (1998)
S. R. Stalp, L. Skrbek, and R. J. Donnelly, Phys. Rev. Lett. 82, 4831 (1999)
H. E. Hall and W. F. Vinen, Proc. Roy. Soc. A238, 215 (1956)
W. F. Vinen and J. J. Niemela, J. Low Temp. Phys. 128, 167 (2002)
K. W. Schwarz, Phys. Rev. B 31, 5782 (1985)
L. Skrbek in Vortices and Turbulence at Very Low Temperatures[Amazon][WorldCat], edited by C. F. Barenghi and Y. A. Sergeev (Springer, New York, 2008), p. 91
M. Tsubota, T. Araki, and S. K. Nemirovskii, Phys. Rev. B 62, 11751 (2000)
B. V. Svistunov, Phys. Rev. B 52, 3647 (1995)
W. F. Vinen, J. Low Temp. Phys. 145, 7 (2006)
E. Kozik and B. V. Svistonov, arXiv:cond-mat/0703047v3 (2007)
D. R. Poole, C. F. Barenghi, Y. A. Sergeev, and W. F. Vinen, Phys. Rev. B 71, 064514 (2005)
G. P. Bewley, D. P. Lathrop, and K. R. Sreenivasan, Nature 441, 588 (2006)
G. P. Bewley, M. S. Paoletti, K. R. Sreenivasan and D. P. Lathrop, Proc. Natl. Acad. Sci. U.S.A. (to be published)
S. Nazarenko, J. Low Temp. Phys. 132, 1 (2003)
C. F. Barenghi, in Vortices and Turbulence at Very Low Temperatures[Amazon][WorldCat], edited by C. F. Barenghi and Y. A. Sergeev (Springer, New York, 2008), p.1

About the Author

Joseph J. Niemela is a member of the permanent scientific staff at the Abdus Salam International Center for Theoretical Physics in Trieste, Italy, where he conducts research in fluid dynamics and low-temperature physics, and coordinates activities in optics and lasers as well as science education. He is also a member of the faculty of the Doctoral School of Environmental and Industrial Fluid Mechanics of the University of Trieste.