Spinning fermions
The field of ultracold atomic gases continues to be driven by the great degree of experimental control over these systems achieved in recent years. In particular, researchers have used this control to better understand phenomena known from conventional condensed-matter physics and to push toward new regimes that cannot be achieved in solid-state materials. In the current issue of Physical Review Letters, X. Du, L. Luo, B. Clancy, and J. E. Thomas of Duke University report on the observation of spin waves—wavelike oscillations in the spin direction well known from studies of ferromagnetism—in trapped gas fermionic atoms [1]. The observed time scales are extremely long, which cannot be explained by the hydrodynamic theory that was successful in describing similar phenomena in Bose gases [2–5]. These results are among the first to explore spin-dependent phenomena with cold-atom Fermi gases, a direction relevant for exploring new regimes of magnetism and spintronics.
With the combination of laser cooling and evaporative cooling it has become possible to achieve temperatures in the micro- to nanokelvin range in atomic gases. This led to the successful creation of an atomic Bose-Einstein condensate in 1995 [6], a discovery that gave birth to the research field of ultracold atomic gases. These gases, which are made up of identical fermions or bosons, or mixtures thereof, are either trapped optically by laser light or magnetically. A magnetic field couples to the total spin of the atoms, which is the sum of their nuclear and electron spin, and leads to splitting of energy levels into so-called hyperfine states.
The energy of each hyperfine state depends on its particular nuclear and electronic spin configuration and on the magnitude of the applied field. The interaction properties of the atoms also depend on the hyperfine states they are in. This makes it possible to tune so-called Feshbach resonances by changing a magnetic field [7]. Specifically, a Feshbach resonance occurs when two atoms collide with a kinetic energy equal to the energy of a bound state of the atoms that is coupled to the colliding atoms by the hyperfine interactions. These resonances enable experimental control over the magnitude and sign of the interaction properties of cold-atom systems, simply by turning a knob that changes the magnetic field strength.
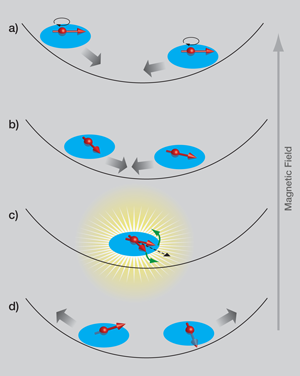
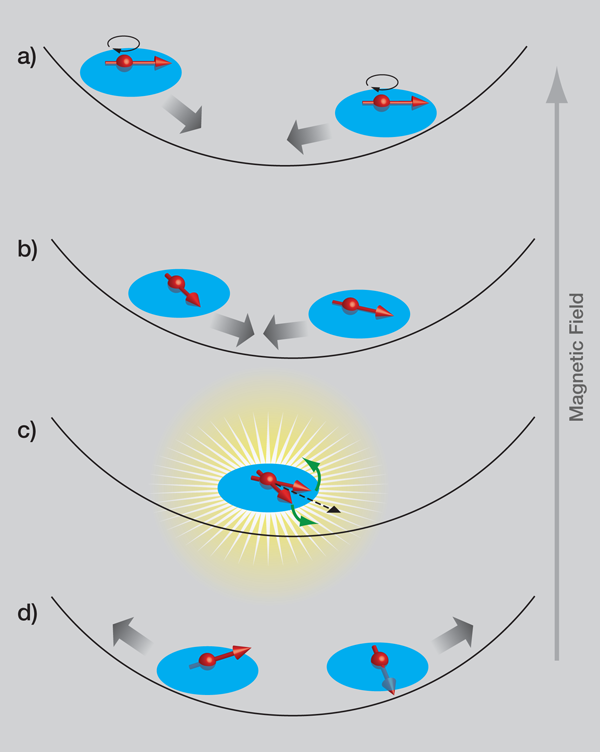
In the experiments by Du et al., atoms in the two lowest-energy hyperfine states of lithium-6 (a fermion) are confined in an optical trap. Because the total spin quantum number is conserved, the other hyperfine states play no role and the atoms behave effectively as spin one-half particles with two spin projections: “up” and “down.” With a radio frequency (RF) pulse tuned to their energy difference the two spin states can be mixed, and Du et al. prepare their system such that every atom is in a coherent superposition of the two hyperfine states (see Fig. 1(a)). Because of the magnetic field used to tune the interatomic interaction via a Feshbach resonance, there is an energy difference between the up and down states which causes the superposition that each atom is in to precess in the plane perpendicular to the magnetic field. The rate of this precession is proportional to the magnetic-field strength, which is not homogeneous but rather varies quadratically across the trap. Atoms at different positions in the sample therefore acquire a different precession angle as shown in Fig. 1(b).
When two atoms, each having a different in-plane precession angle, collide, the interaction conserves their total spin. The spins of the individual atoms do change, however, because of so-called exchange interactions that cause the spins of the individual atoms to precess around each other (Fig. 1(c)). This causes the atoms to acquire an out-of-plane spin component along the magnetic field. Atoms at different positions (and therefore different spin precession angles) in the trap have different velocities, which correlates the spin direction with the velocity. This causes a spin current in the system: ultimately atoms with out-of-plane spin aligned with the magnetic field move in one direction, the atoms with opposite spin move in the other. The absorption imaging commonly used to obtain density profiles of trapped atomic vapors is sensitive to hyperfine states, which allows separate imaging of the two states. In the experiment, the spin wave that is set up by the spin current is therefore observed as spin segregation, where one spin species moves to the edges of the atomic cloud. The sign of the exchange interaction determines the precession angle in the atomic collision and, therefore, whether up or down atoms move to the edge. This is nicely confirmed by Du et al. by using the Feshbach resonance that tunes the interactions.
The experiments of Du et al. were carried out at temperatures of about , which for their densities implies that they are in the nondegenerate regime in which there is not much difference between bosons and fermions in equilibrium. Their results, therefore, are at first sight similar to experiments carried out with bosons [2]. A spectacular difference, however, is in the time scales in both experiments. With bosons the spin segregation was found to decay after a few hundreds of milliseconds. However, Du et al. find that the spin waves with fermions can persist for times of up to five seconds. To make a more quantitative comparison, Du et al. have applied the theory that was successful in explaining previous results obtained with bosons [3–5] to their experiments. They find that the theory is not suitable to explain the time scale and amplitude of the observed effect quantitatively, although there is some qualitative agreement. The key difference is most likely that, because of the Pauli exclusion principle, fermionic atoms at low temperatures have a much harder time interacting and coming to equilibrium than their bosonic counterparts. Furthermore, the interaction between different hyperfine states is weak in the experimental situation of Du et al. As the theoretical approach is hydrodynamical in nature and therefore hinges on strong collisions that enforce local equilibrium, it is perhaps not immediately suited to treat this experimental situation. A quantitative explanation of the experiments would have to take into account the possible far-from-equilibrium situations and has not yet been worked out.
The physical basis for the spin segregation observed by Du et al. is the formation of spin currents and spins that precess about each other while conserving their total spin angular momentum. In the field of spintronics, similar phenomena give rise to spin transfer, where a spin current is used to excite or reverse a nanomagnet [8,9], a concept that is relevant for future magnetic-memory applications. These experimental results are a first step in exploring cold-atom analogues of spin transfer and show that it can be studied in a regime of long relaxation times that could never be achieved with ordinary ferromagnetic materials because of dissipation mechanisms that are not present in cold-atom systems. Of course, to really study the physics of ferromagnetism and its interaction with a spin current, the Fermi gas should undergo a transition to spontaneous spin polarization, which has not yet been observed and which requires strong repulsive interactions [10]. So far, most experiments with cold fermionic atoms have focused on attractive interactions where the Bardeen-Cooper-Schrieffer state occurs. This state underlies superconductivity, one of the two most important phase transitions in condensed-matter physics. The other is ferromagnetism and the observation by Du et al. of spin waves in a Fermi gas is an important step towards exploring spin-dependent phenomena, and possibly ferromagnetism, in these systems.
References
- X. Du, L. Luo, B. Clancy, and J. E. Thomas, Phys. Rev. Lett. 101, 150401 (2008)
- H. J. Lewandowski, D. M. Harber, D. L. Whitaker, and E. A. Cornell, Phys. Rev. Lett. 88, 070403 (2002)
- M. Ö. Oktel and L. S. Levitov, Phys. Rev. Lett. 88, 230403 (2002)
- J. N. Fuchs, D. M. Gangardt, and F. Laloë, Phys. Rev. Lett. 88, 230404 (2002)
- J. E. Williams, T. Nikuni, and C. W. Clark, Phys. Rev. Lett. 88, 230405 (2002)
- M. H. Anderson, J. R. Ensher, M. R. Matthews, C. E. Wieman, and E. A. Cornell, Science 269, 198 (1995)
- E. Tiesinga, B. J. Verhaar, and H. T. C Stoof, Phys. Rev. A 47, 4114 (1993)
- J Slonczewski, J. Magn. Magn. Mater. 159, L1 (1996)
- L. Berger, Phys. Rev. B 54, 9353 (1996)
- R. A. Duine and A. H. MacDonald, Phys. Rev. Lett. 95, 230403 (2005)