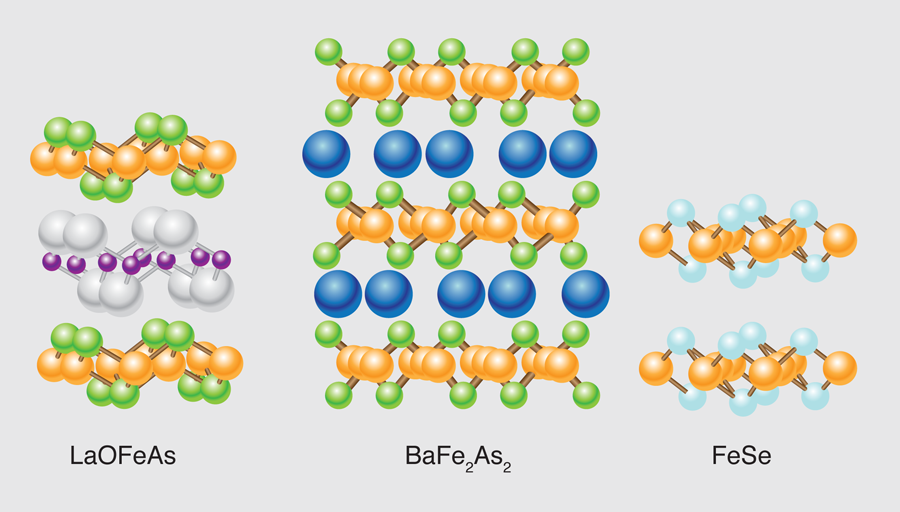The iron age of superconductivity

Michelle Johannes

Viewpoint

The iron age of superconductivity

Center for Computational Materials Science, Code 6390, Naval Research Laboratory, Washington DC 20375, USA

October 13, 2008• Physics 1, 28

The discovery of superconductivity in iron-based compounds with a similar, but simpler, structure to the iron-pnictides could provide an important testing ground for unconventional superconductivity.

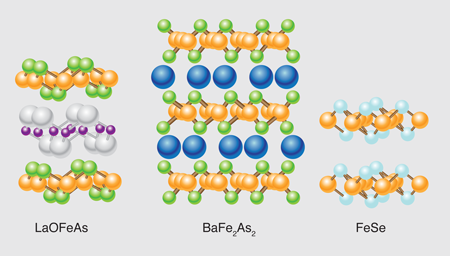
Figure caption — **Figure 1:** Even though it has a much simpler crystal structure, FeSe (right) has many of the same magnetic and electronic properties (including superconductivity) as the iron-based pnictide superconductors (left, center). Fe (orange), As (green), La (white), O (purple), Ba (dark blue), Se (light blue).

The discovery less than one year ago of superconductivity with $T_{c} = 26 K$ in doped $LaOFeAs$ [1] began a wave of research into the iron-based “pnictide” family of superconductors that quickly pushed the transition temperature to its current record of 56 K [2]. Interestingly, what we have learned so far about these materials is that they do not resemble conventional superconductors, nor do they operate according to the same underlying physics found in the high $T_{c}$ cuprates (for a useful review, see [3]). Writing in Physical Review B, Alaska Subedi, Lijun Zhang, David Singh, and Maohua Du of Oak Ridge National Laboratory in the U.S. [4] show that the electronic, magnetic, and structural effects relevant to superconductivity in the iron-based pnictides are also present in $FeSe$ . Like the pnictides, this material superconducts when doped and the Fe atoms are tetrahedrally coordinated. Yet what is interesting about this iron-based compound is that its structure is substantially simplified compared to the pnictides (see Fig. 1). In particular, $FeSe$ has a chalcogen anion, and no intercalating plane of atoms, such as the LaO plane in the pnictides (the central plane of atoms in Fig. 1, left), where the doping usually occurs. This establishes that the operative physics takes place in doped $Fe X$ tetrahedral planes ( $X$ =pnictogen or chalcogen) and that intercalant layers are conclusively inert. This provides the opportunity to study this intriguing new type of superconductivity using the simpler $FeSe$ series [where $Se$ can be replaced by other chalcogens, such as sulfur ( $S$ ) and tellurium ( $Te$ )], which are both easier and, because they contain no arsenic, safer to synthesize.

How will exploring this class of materials help us to better understand unconventional superconductivity, particularly in the pnictides? In conventional superconductors, the mechanism that binds electrons together to form “Cooper pairs” is electron-phonon coupling. If electrons respond strongly to lattice distortions (phonons), then the coupling is strong. This increases the tendency toward pairing and raises the superconducting transition temperature. A formula has been developed for figuring out the transition temperature in terms of the electron-phonon coupling $λ$ , the logarithmically averaged phonon frequency $ω_{ln}$ , and the effective Coulomb repulsion $μ^{*}$ . Subedi et al. calculate that, even taking the lowest reasonable estimate of $μ^{*}$ , the strength of the electron-phonon coupling in $FeSe$ can only produce transition temperatures of less than 1 K, which is an order of magnitude below what is observed. This places $FeSe$ in the category of unconventional superconductivity, along with $LaOFeAs$ , which was earlier shown to have a similarly weak electron-phonon coupling compared to its $T_{c}$ [5,6]. Interestingly, despite being isostructural to LaOFeAs, the transition temperature of the non-iron-based superconductor $LaONiP$ can be accurately accounted for by electron-phonon coupling [7]. This indicates that the specific chemistry of the $Fe$ atom is a nontrivial factor in the physics of this new family.

Once electron-phonon coupling has been eliminated as the superconducting mechanism, the next logical direction to explore is magnetic fluctuations. In the same way that lattice vibrations, which are essentially charge fluctuations, can mediate an effective attractive interaction between electrons, fluctuations in the spin channel can accomplish the same thing. In the iron-based pnictides, the ground state of undoped compounds is a spin-density wave—a spatial modulation of the electron spin that extends throughout the material. Doping the intercalant plane (by substituting some $F$ for $O$ , for example) or applying pressure, destroys the spin-density wave and allows the superconducting phase to occur. The superconductivity is never concurrent with the spin-density wave, but the two are always near one another, indicating that they are likely competitive phases. Because spin fluctuations grow strongest just before a magnetic transition, this could signal a necessary role for fluctuations in creating Cooper pairs.

There is good evidence that strong magnetic fluctuations are indeed present in the pnictides. First, there is the experimental evidence from resistivity and spectroscopic data [8,9]. Second, the measured magnetic moments on the $Fe$ atoms of pnictides are substantially smaller than those calculated using density-functional theory. The fact that calculation and measurement disagree is not itself particularly unusual, but the direction of disagreement is surprising. While density-functional methods are known to frequently underestimate the moment in magnetic compounds (most dramatically in strongly correlated systems where the magnetism stems from localized $d$ or $f$ atomic states), in the pnictides, the theory substantially overestimates the magnetic moment [10,11]. This can happen in materials where the magnetic moment fluctuates in time. Since experimental measurements probing the magnetic moment take place over a finite interval of time, the observed magnetic moment is actually an average over all moments that occur during the time of observation. Density-functional theory, on the other hand, is a static approximation. No account is made for time variation in the magnitude or direction of the moment. The strongly depressed value of the measured moment compared to calculation can therefore be nicely explained by strong fluctuations.

Where do appreciable spin fluctuations come from? One mechanism is Fermi-surface nesting. This phenomenon occurs when a vector in reciprocal space—the space defined by the electrons’ momenta rather than their position—connects substantial portions of a Fermi surface (or connects separate Fermi surfaces). Subedi et al. show that the same tendency toward Fermi-surface nesting seen in the pnictides exists also in the $FeSe$ family. Interestingly, very strong nesting will favor a spin-density wave state, whereas weaker or partial nesting will favor pairing via spin fluctuations. Because the shape of the Fermi surfaces and thereby the strength of nesting can be changed by manipulating the electron count, the balance between the spin-density wave state and the superconducting state can be tipped by doping. The Fermi-surface shape can also be changed by pressure, perhaps explaining the strong pressure and doping dependencies of $T_{c}$ in both pnictides and $FeSe$ .

Density-functional calculations have been shown to be successful at reproducing the experimentally observed spin-density wave ground state as well as an accompanying structural transition in pnictides [12]. The success of these calculations gives credence to Subedi et al.’s prediction that the same magnetic ordering should be the ground state of $FeSe$ , $FeTe$ , and perhaps $FeS$ . They show that the tendency of $FeTe$ to adopt a spin-density wave state is quite a bit stronger than that of $FeSe$ . This points to $FeTe$ having an even higher transition temperature if spin fluctuations are behind the superconductivity and if, like its $Se$ analogue, $FeTe$ can be doped.

The revelation that the fundamental interactions present in the iron-based pnictides are also present in the simple structure of $FeSe$ essentially gives researchers an entirely new family of compounds in which to explore both superconducting and normal state properties. Researchers have already pushed the original 8 K transition temperature [13] in $Se$ -deficient $FeSe$ to 27 K by using pressure [14]. Now, Subedi et al. calculate that $FeTe$ may be coaxed to give an even higher $T_{c}$ . Research along this direction is only just beginning, but the work of Subedi et al. establishes that these materials, in addition to serving as a useful tool for study of the physics of pnictides, could themselves prove to be remarkable superconductors.

References

Y. Kamihara, T. Watanabe, M. Hirano, and H. Hosono, J. Am. Chem. Soc. 130, 3296 (2008)
C. Wang, L. Li, S. Chi, Z. Zhu, Z. Ren, Y. Li, Y. Wang, X. Lin, Y. Luo, S. Jiang, X. Xu, G. Cao, and Z. Xu, Europhys. Lett. 83, 67006 (2008)
M. Norman, Physics 1, 21 (2008)
A. Subedi, L. Zhang, D. J. Singh, and M. H. Du, Phys. Rev. B 78, 134514 (2008)
L. Boeri, O. V. Dolgov, and A. A. Golubov, Phys. Rev. Lett. 101, 026403 (2008)
D. J. Singh and M-H. Du, Phys. Rev. Lett. 100, 237003 (2008)
A. Subedi, D. J. Singh, and M-H. Du, Phys. Rev. B 78, 060506 (2008)
M. A. McGuire, A. D. Christianson, A. S. Sefat, B. C. Sales, M. D. Lumsden, R. Jin, E. A. Payzant, D. Mandrus, Y. Luan, V. Keppens, V. Varadarajan, J. W. Brill, R.P. Hermann, M. T. Sougrati, F. Grandjean, G. J. Long, arXiv: 0806.3878
F. Bondino, E. Magnano, M. Malvestuto, F. Parmigiani, M.A. McGuire, A.S. Sefat, B.C. Sales, R. Jin, D. Mandrus, E.W. Plummer, D.J. Singh, and N. Mannella, arXiv:0807.3781
I. I. Mazin, M. D. Johannes, L. Boeri, K. Koepernik, and D. J. Singh, Phys. Rev. B 78, 085104 (2008)
Z. P. Yin, S. Lebègue, M. J. Han, B. P. Neal, S. Y. Savrasov, and W. E. Pickett, Phys. Rev. Lett. 101, 047001 (2008)
A. Jesche, N. Caroca-Canales, H. Rosner, H. Borrmann, A. Ormeci, D. Kasinathan, K. Kaneko, H.H. Klauss, H. Luetkins, R. Khasanov, A. Amato, A. Hoser, C. Krellner, C. Geibel, arXiv:0807.0632
F. C. Hsu, J. Y. Luo, K. W. Yeh, T. K. Chen, T. W. Huang, P. M. Wu, Y. C. Lee, Y. L. Huang, Y. Y. Chu, D. C. Yan and M. K. Wu, arXiv:0807.2369
Y. Mizuguchi, F. Tomioka, S. Tsuda, T. Yamaguchi and Y. Takano, arXiv:0807.4315

About the Author

Michelle Johannes received her Ph.D. in Computational Physics in 2003 from the University of California, Davis. Her work there on superconductivity and magnetism continued during her postdoctoral fellowship at the Naval Research Laboratory in Washington D.C., where she became a permanent staff member in 2005. In addition to continuing work on superconducting materials, her current interests include magnetism on triangular lattices and the electrochemistry of oxide battery materials.