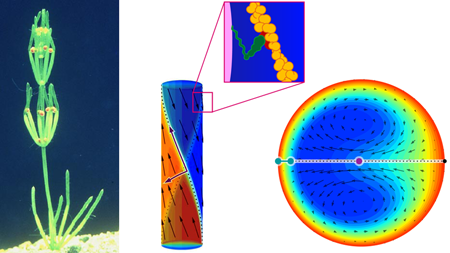
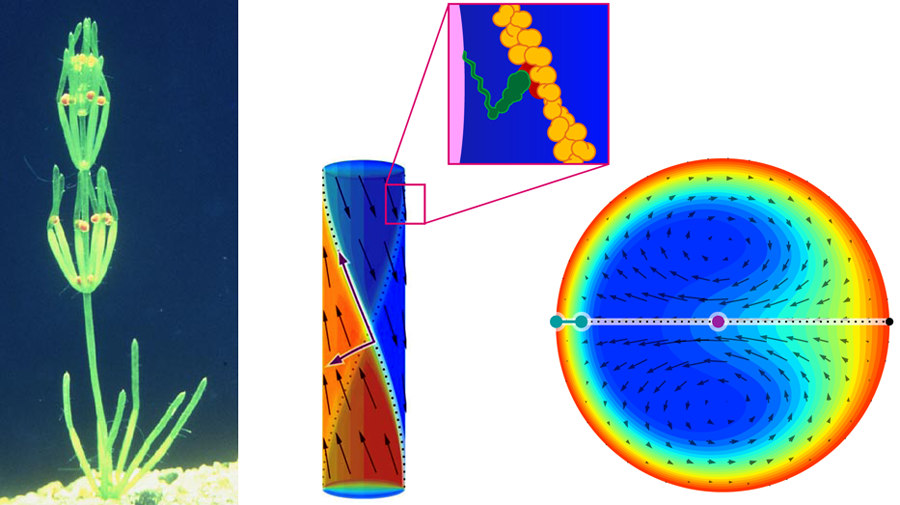
The inner life of mesoorganisms
The physical world as experienced by microorganisms looks and feels very different than the one we perceive every day—so different, in fact, that the strategies evolved by small creatures to perform life’s basic functions in their world would not be effective in ours. Writing in Physical Review Letters, Jan-Willem van de Meent, Idan Tuval, and Raymond Goldstein of the University of Cambridge have analyzed the inner workings of a curious set of aquatic plants (see Fig. 1), in which single cells have radii on the order of hundreds of microns and lengths on the order of centimeters [1]. Such “mesoorganisms” find themselves in an odd position: their cells are large enough that standard microorganism strategies for transporting nutrients through the cell interior are unacceptably slow, yet small enough that the strategies employed by us “macrobeasts” are overwhelmed by viscous damping and also do not work. The group’s study provides a fascinating window into a very different biophysical world than is usually considered in biophysics (namely that of a single molecule or bacteria). Furthermore, the length scales and aspect ratios they consider are essentially identical to those of microfluidic devices—suggesting biomimetic strategies for transport and mixing based on those evolved by these tiny plants about a half-billion years ago.
In his now classic lecture “Life at Low Reynolds Number,” Nobel Laureate Edward Purcell used basic physical observations to lay out a series of compelling observations about the counterintuitive world in which microorganisms live [2]. On the micron length scales relevant to bacteria and most other single-celled organisms, the viscous forces encountered as they move through water render inertia essentially irrelevant: when a bacterium stops spinning its flagella, it only glides for about a microsecond, during which time it travels less than an angstrom! Clearly, the strategies that these simple microorganisms evolved to move themselves through their fluid environment differ substantially from most multicellular organisms.
These simple physical observations about the micron-scale, viscosity-dominated world lead to profound consequences for micron-scale life. How should microorganisms eat, find friends, or dispose of waste? Microbes can collect far more nutrients by diffusion alone than by swimming to scoop them up. So, if the act of swimming doesn’t increase food uptake, then why bother swimming? Some microorganisms don’t; others do to find “greener pastures” that are richer in nutrients. Diffusion also dominates chemoreception—the manner in which microorganisms sense the chemical world around them. A relatively small number of chemoreceptor proteins, well separated on a cell surface, is as efficient as a surface completely covered in chemoreceptors [3].
Diffusion within simple microorganisms is typically fast enough to render directed transport (along microtubles, etc.,) unnecessary for food, waste, information, and proteins to work their way in and out of the cell. Larger organisms, of course, use a hierarchical set of structures, where large-scale (inertial) flows are actively driven through, for example, airways and arteries, and progressively into smaller spaces, until such time as diffusion takes over (for example, across alveoli in the lungs or through capillary walls into cells).
This sets the stage for the Cambridge group, who have identified and analyzed a variety of mesoorganisms that contain unusually large cells. They study the plant Chara corallina (Fig. 1), in which cylindrical cells, a few hundred microns in diameter and centimeters in length, link together to form branches of the plant. Although large compared with most cells, the cells of these plants are small enough that viscous stresses render inertia irrelevant and turbulent mixing out of the question as mechanisms to transport nutrients throughout the cell. At the same time, however, Chara cells are large enough that diffusive transport of nutrients and wastes would be too slow for the plant to stay alive.
How can such a large, single cell drive the steady flows required for life, without the benefit of “macroscopic” moving parts like pumps or muscles? These transport challenges require an altogether different strategy. Approximately 500 million years ago, Chara and its relatives evolved a technique, cyclosis, to drive a steady flow of cytoplasm within the cell walls. It employs the molecular machinery familiar to mainstream biophysicists—the molecular motor myosin, which pulls cargo along actin filaments that serve as its track—but with a decidedly non-mainstream twist. Actin filaments spiral along the walls of Chara cells in a helical fashion, with two distinct hemicylinders oriented in opposite directions (Fig. 1, center). As the myosin motors traverse the filaments with their cargo, the moving cargo pulls the (viscous) fluid along with it, effectively establishing fluidic “conveyor belts” along the walls. The long-range nature of viscous (Stokes) flows ensures the influence of the walls is felt throughout the cell (Fig. 1, right). Cyclosis flows are, in this regard, the biophysical analog of electro-osmotic flows [4–6].
van de Meent et al. established and solved a model for cyclosis that describes two counter-directed, helically wrapping “conveyor belts” driven along the walls of a cylinder. Although the geometry can be described simply, the calculation itself is rather untraditional—after all, the flow is itself helical, which is not easily captured by any of the standard coordinate systems or typical eigenfunctions for Stokes flows. By introducing a natural helical coordinate system, they found simple expressions for the most dominant eigenmode—which corresponds to two helically-intertwined dipolar vortices, wherein fluid flows quickly from one wall to the other. Their technique is itself significant, as it provides a natural fashion to treat Stokes flows with helical symmetry.
Armed with this velocity field, they then compared diffusive and convective transport of solute within the cell. The vortical flows take solute across the cell far faster than diffusion would—this is a consequence of the cell’s long length scales. In addition to enhanced mass transport to the walls, they found a reduction of Taylor dispersion [5]—an axial convective dispersion that typically transforms a nice “plug” of sample into a “diffusively” growing blob. The reduction occurs because the vortical velocity fields force solute to sample all streamlines more quickly than diffusion alone would.
This brings us back to the issue of biomimetic strategies that borrow nature’s designs to engineer useful devices. Strategies to increase mass transport rates in microchannels, for example, will be essential for rapid sensing of extremely dilute systems [7]. In microfluidics, the “staggered herringbone mixer” [8] incorporates ridges along the walls to drive counter-rotating, helical flows to enhance mixing across the channel, while reducing dispersion along the channel. The mesoorganisms studied by van de Meent et al. illustrate a case where nature, faced with a similar problem, found a similar solution. Hundreds of millions of years later, in developing new microfluidic technologies, humans have found solutions that are not so far from those evolved in nature. Even though the methods for driving the flows are different (pressure-driven vs “cargo-driven,” and chaotic vs regular), the resulting double-helical flows share much in common.
While much of biophysics has been devoted to single-molecule and molecular-level studies, many mysteries remain on larger scales, at the cell level and above, where perceptive questions and keen physical insight reveal many surprises and useful insight into nature’s bag of tricks. van de Meent et al. nicely highlight the interesting and potentially important implications of cyclosis, and more generally the seemingly endless supply of fascinating physical processes at work in biological systems of all scales.
References
- J-W. van de Meent, I. Tuval, and R. E. Goldstein, Phys. Rev. Lett. 101, 178102 (2008)
- E. M. Purcell, Am. J. Phys. 45, 3 (1977)
- H. C. Berg and E. M. Purcell, Biophys. J. 20, 193 (1977)
- R. B. Schoch, J. Han, and P. Renaud, Rev. Mod. Phys. 80, 839 (2008)
- T. M. Squires and S. R. Quake, Rev. Mod. Phys. 77, 977 (2005)
- H. A. Stone, A. D. Stroock, and A. Ajdari, Annu. Rev. Fluid Mech. 36, 381 (2004)
- T. M. Squires, R. J. Messinger, and S. R. Manalis, Nat. Biotechnol. 26, 417 (2008)
- A. D. Stroock et al., Science 295, 647 (2002)