The primordial power spectrum revisited

Carlos Barceló

Viewpoint

The primordial power spectrum revisited

Andalusian Institute of Astrophysics (CSIC), Granada, Spain

October 20, 2008• Physics 1, 31

The universe we see today is the result of mass-energy fluctuations during the rapid inflationary expansion that followed the big bang. A new approach to analyzing those fluctuations brings theory into better alignment with observational data.

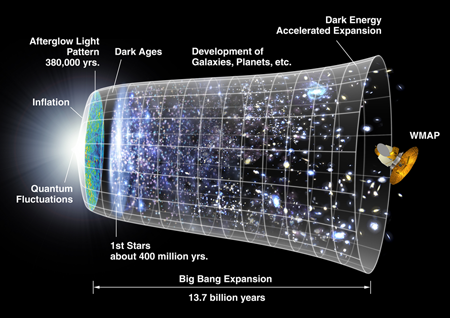
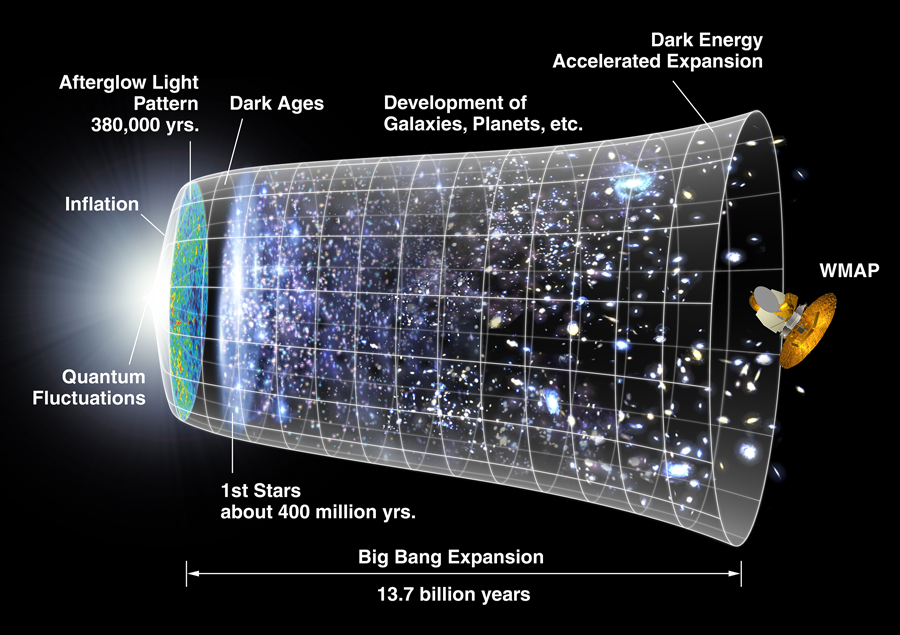
Figure caption — **Figure 1:** A schematic model of the evolution of the universe from the big bang to the present. Quantum fluctuations just after the big bang develop during the rapid period of inflationary expansion into the inhomogeneities that lead to formation of stars and galaxies. Agulló *et al.* [3] propose a new definition of the distribution of primordial fluctuations that overcomes some of the problems of the inflationary model.

A period of rapid expansion (called inflation) in the early stages of the Universe is believed to be responsible for the generation of inhomogeneities in the distribution of matter [1]. These primordial inhomogeneities have evolved to form all the structures that we observe in the Universe, from the inhomogeneities in the cosmic microwave background to galaxies, stars, and planets (Fig. 1). However, calculations of the primordial distribution of inhomogeneities (or fluctuations) lead to values for their magnitudes that are too large unless the parameters of the models of inflation acquire seemingly unnatural values [2]. Writing in Physical Review Letters, Iván Agulló and José Navarro-Salas (University of Valencia), Gonzalo Olmo (Perimeter Institute and Institute of Materials Science, Madrid), and Leonard Parker (University of Wisconsin) argue that this problem might be alleviated if the physical spectrum of inhomogeneities was not the one usually assumed, but a modified version of it [3].

Some 13.5 billion years ago the whole Universe that we observe today was concentrated in an extremely tiny volume. All the observations we have, together with their interpretation in terms of general relativity and quantum mechanics, confirm this. At some moment the Universe started to inflate, rapidly doubling its volume every $\sim 10^{- 39} s$ (the precise numbers depend on the specific model). In only approximately 60 of these time intervals the Universe acquired a huge volume (although still much smaller than it is today) becoming a vast and extremely homogeneous space with no trace of matter. Matter appeared later (as a product of the decay of the fields responsible for driving the inflation) in a process called reheating.

However, the Universe cannot have been completely homogeneous or else there would have been nothing to give birth to the density contrasts characterizing the structures that we see today. Certainly the Universe became very homogeneous after inflation but not completely. The violent dynamics of inflation itself were enough to create quantum inhomogeneities from the vacuum. As is well known, the quantum vacuum can be visualized as a fluctuating entity in which all sorts of virtual pairs of particles are continuously being created and annihilated. (Here I use the word “particles” generically, meaning any quanta associated with any field present in the Universe, in particular with the fields describing departures from homogeneity of the geometry.) In addition, one can think of each individual virtual particle as characterized by a frequency (directly proportional to its virtual energy). If the curvature of spacetime changes with time, some of these virtual pairs can absorb energy and become real. This is what is supposed to have happened during inflation.

Consider virtual particle-antiparticle pairs at the start of the inflationary period having a frequency $ν = E / h$ (where $E$ is the virtual particle energy and $h$ is Planck’s constant) that is larger than the Hubble frequency scale $H$ (this is an almost constant frequency scale that characterizes the rapidity of inflation). As inflation develops, the frequency of these virtual pairs gets rapidly red-shifted by the expansion. At some moment of the inflationary period, this virtual particle frequency becomes comparable to the Hubble frequency scale. It is then that the dynamics of inflation enters in resonance with these virtual pairs, transferring energy to the pairs and making them real. Associated with each frequency there is a wavelength, which in this case gives us a measure of the average spatial extent of an inhomogeneity. In this way, during inflation, a primordial spectrum of inhomogeneities (or particles) is produced. (In analogy with the spectral analysis of electronic signals, this has come to be called a “power spectrum.”)

This is the physical picture, but technically what do we define as the primordial power spectrum? The standard definition of the power spectrum over time $| δ_{k} (t) |^{2}$ is essentially the Fourier transform of the two-point correlation function associated with the initial vacuum state (where $k$ represents the comoving wave number associated with each particle). This provides essentially a description of the typical magnitude of the inhomogeneities of spatial extent $2 π / k$ at different times. For the case of a universe undergoing an exponential or de Sitter inflation (after the so-called de Sitter solution to Einstein’s equations, which cosmologists often use as a starting point because it is a geometry with many symmetries and so one in which calculations can be done analytically), one finds that at the end of the inflationary era a power spectrum $| δ_{k} |^{2} \sim ħ H^{2} / 2 π$ has been generated [3,4].

From the analysis of the correlations in the Cosmic Microwave Background (CMB) data we know that the primordial power spectrum has to be (nearly) scale invariant (that is, it cannot depend on $k$ ) [5]. This is precisely the result of the previous calculation, which is often considered the most important prediction of inflation [6]. However, the same CMB data tell us that the magnitude of the primordial power spectrum has to be of the order of $10^{- 5}$ . This latter observation is not naturally reproduced by inflation; in the previous expression, for example, the Hubble frequency scale during inflation cannot be made small enough.

The central point of work reported by Agulló et al. is to propose an alternative definition of the primordial power spectrum in which the previous two-point function is substituted by the subtraction of two different two-point functions associated with two different quantum states. Although the authors don’t say it explicitly, their analysis suggests that the two quantum states should be chosen to be a natural vacuum state before inflation and a natural vacuum state after inflation (note that in curved spacetimes the same quantum state can appear as vacuum, or empty of particles, for some observers and as a nonvacuum state for others). With the standard definition of the power spectrum one obtains a nonzero $| δ_{k} |^{2} \neq 0$ , even in the absence of inflation. Instead, with this new definition in the absence of inflation both quantum states almost coincide, so that one would obtain $| δ_{k} |^{2} \sim 0$ , which makes more sense. Thus the new definition removes spurious contributions from the power spectrum.

The explicit calculations in the paper are done in an eternal de Sitter space, so the authors illustrate their proposal by using for the two quantum states the natural de Sitter vacuum and one of the equivalent comoving vacua (selected because it sets the reference for a local future observer). In particular, they show that by using their subtraction prescription, the main contribution to the power spectrum depends not on the Hubble frequency scale, but on the mass of the field-driving inflation (the proposed field of particles called inflatons).

In this situation Agulló et al. find that the new power spectrum can still be scale invariant but orders of magnitude smaller than the standard one, thus alleviating the problem of concordance with the magnitude of the inhomogeneities in the CMB. However, it remains to be seen whether this suppression effect continues to be present in more realistic models of inflation. Also, we must determine whether the suppression depends strongly on specific characteristics of those models or whether, on the contrary, it is quite generic. Further work will be needed to sort out these questions.

References

See, for example, the review by A. Linde, Prog. Theor. Phys. Suppl. 163, 295 (2006)
See, for example, V. F. Mukhanov, H. A. Feldman, and R. H. Brandenberger, Phys. Rep. 215, 203
I. Agulló, J. Navarro-Salas, G. J. Olmo, and L. Parker, Phys. Rev. Lett. 101, 171301 (2008)
G. W. Gibbons and S. W. Hawking, Phys. Rev. D 15, 2738 (1977)
E. Komatsu et al. (WMAP Collaboration), arXiv:0803.0547
The first calculation of the primordial power spectrum appeared in V. F. Mukhanov and G. V. Chibisov, JETP Letters 33, 532 (1981); it was soon followed by S. W. Hawking, Physics Letters B 115, 295; A. H. Guth and S-Y. Pi, Phys. Rev. Lett. 49, 1110 (1982); A. A. Starobinsky, Physics Letters B 117, 175; J. M. Bardeen, P. J. Steinhardt, and M. S. Turner, Phys. Rev. D 28, 679 (1983)

About the Author

Carlos Barceló is a staff member at the Andalusian Institute of Astrophysics (CSIC), Granada, Spain. Previously, he was a postdoctoral researcher at Washington University in St. Louis, and at the Institute of Cosmology and Gravitation of Portsmouth University in the UK. His research interests include the analysis of semiclassical corrections to classical configurations in general relativity. He is currently very much involved in the analogue gravity program: Obtaining insights on quantum gravity by analyzing analogue properties in condensed-matter systems.