A new phase in quantum computation
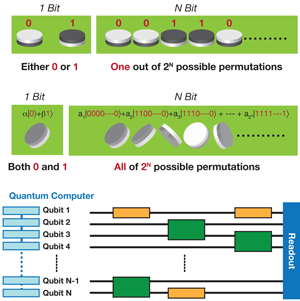
Peter Shor’s demonstration [1] in the mid 1990s of an efficient algorithm for factorizing prime numbers has triggered an immense interest in various aspects of quantum computation. Researchers have proposed several ways to implement quantum computers, ranging from systems that store information in trapped atoms [2] or ions [3] to computers based on condensed matter systems such as Josephson junctions [4] and quantum dots [5]. Such computers would rely on the phenomena of quantum coherence and quantum entanglement among a set of such “qubits” (Fig. 1). Despite these efforts, quantum computers of any useful size still seem far beyond the scope of present day technology, mainly because of the difficulties in maintaining the necessary coherence of all the qubits. Achievable error probabilities for qubit manipulations are still far above the value of required for efficient fault-tolerant quantum computation [6]. A key challenge for quantum computation research is to achieve this precision.
One approach towards this goal is to use quantum geometric phases (that is, the effects of moving a set of quantum parameters around a curved parameter space) [7–9] to implement quantum gates that manipulate states of physical qubits. Such gates would be the quantum computing equivalent of the logic gates found on today’s microchips. The idea of using geometric phase is known as holonomic or geometric quantum computation, and has become one of the key approaches to achieving quantum computation that is resilient against errors. In 1999, Zanardi and Rasetti [10] laid the theoretical foundations of holonomic quantum computation by showing that any quantum circuit can be generated by using suitable Hamiltonians that depend on experimentally controllable parameters, such as those related to the manipulation of a bosonic mode in a quantum optical system [11]. At the same time, Jones et al. [12] demonstrated experimentally a quantum gate based on geometric phase that was able to entangle a pair of nuclear spins in a nuclear magnetic resonance (NMR) setup. This experiment provided the first explicit example of geometric quantum computation and helped to boost the interest in this field.
Holonomic quantum computation
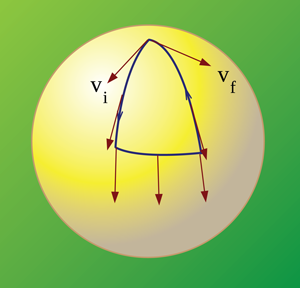
A quantum holonomy or geometric phase is the quantum analogue of a well-known rotation effect in differential geometry that arises when a vector is parallel transported around a loop on a curved surface (see Fig. 2). This vector may return rotated although there has been no local rotation along the loop. Such a “global rotation without local rotation” is the holonomy caused by the curvature of the underlying space. In quantum mechanics, states are represented by vectors in a Hilbert space and rotations of such vectors are given by applying unitary matrices or phase factors to them. Just as in the differential geometric case, a quantum state vector can be transported without locally rotating it around a loop in some quantum parameter space, and the resulting transformation has the same effect on the state vector as applying a unitary matrix [7] or phase factor [8,9] that depends only on the global geometric properties of the loop.
In the original form of holonomic quantum computation [10], the states of the quantum bits (the qubits) are encoded in a degenerate energy eigenspace of a suitable parameter-dependent Hamiltonian. When the parameters change adiabatically around a loop, a state that starts in such an energy eigenspace of the initial Hamiltonian will end at another state in the same eigenspace. The final and initial states of the qubits will be related by a unitary rotation that depends only on the properties of the loop in parameter space, but is independent of the energy of the state and the time it takes to traverse the loop. This rotation is the desired holonomy transformation that constitutes the holonomic quantum gate—the basic building block of holonomic quantum computation. This is very different from the more conventional kind of quantum computing where qubits in a register of some kind are acted upon by various logic operations to dynamically evolve the system in time toward a result. Geometric quantum computation, which is discussed in the next section, is holonomic quantum computation, or some nonadiabatic extension thereof, restricted to nondegenerate (one-dimensional) energy eigenspaces of Hamiltonians.
In practice, to perform quantum computation it is sufficient to implement certain elementary one- and two-qubit operations, forming universal sets. These operations are analogous to the fundamental building block OR, AND, NOT operations of conventional microelectronics. Such a set of operations on qubits can be used to simulate any quantum computation with arbitrary precision. A first goal for holonomic quantum computation is to find physical implementations of universal sets of gates that are all-geometric, i.e., based entirely upon quantum holonomies.
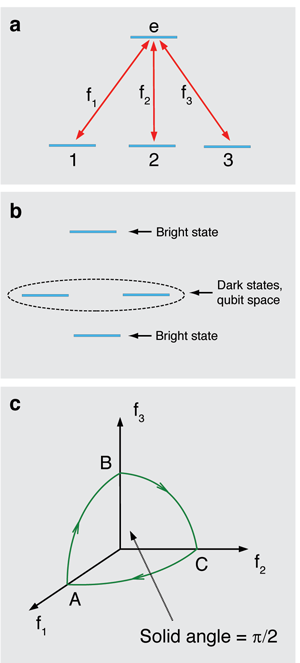
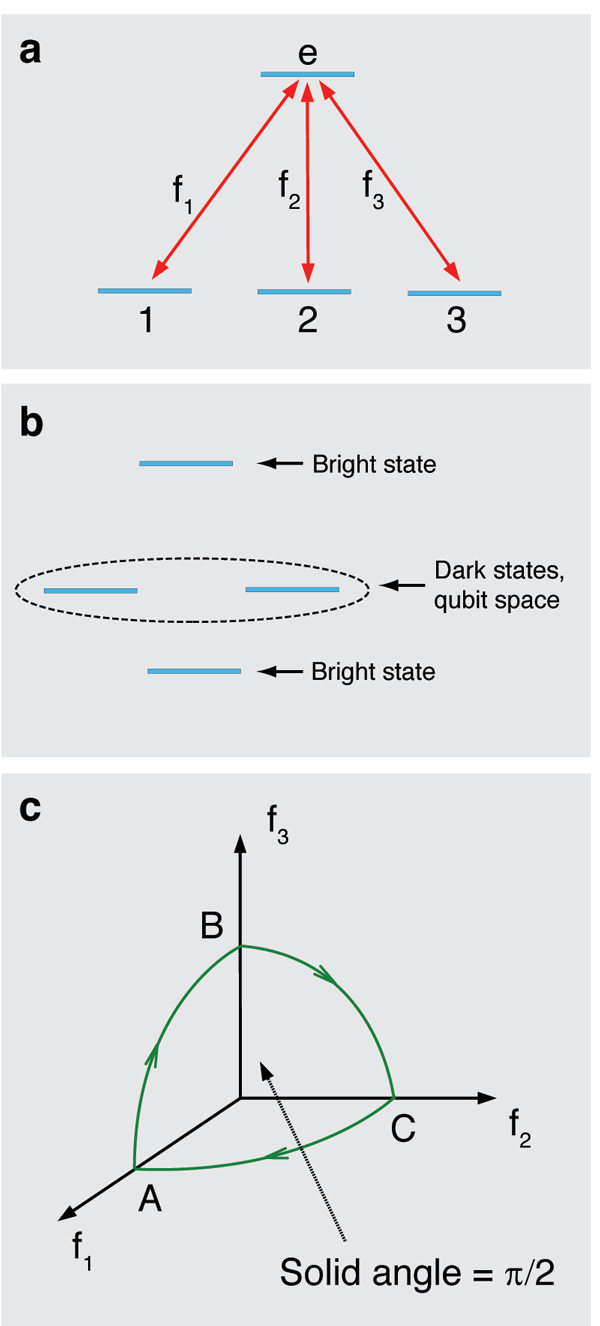
Basically what we are looking for are physical qubits (two-level quantum systems) whose evolution can be controlled by means of parameters in a curved space. Unanyan et al. [13] discovered that a four-level atom forming a “tripod” system (see Fig. 3) could represent a curved parameter space. This system consists of three degenerate internal atomic states, each state coupled to an excited state by a laser field. The fields lift the degeneracy of the internal states, but only partially: two of the energy levels remain degenerate for all field configurations. These degenerate levels have zero energy and do not involve the excited state, i.e., they form a pair of “dark” states that can be used to encode the states of a single qubit.
One can perform computation on the qubit if the amplitudes and phases of the laser fields are varied around suitable loops. In this way, one can achieve a pair of noncommuting holonomic gates that are universal for the qubit. Next, if the atoms that store the different qubits are allowed to interact, and the fields are varied around a suitable loop, the result is an entangling two-qubit gate of purely geometric origin, which completes the all-geometric universal set.
Remarkably, the above-described scenario for purely geometric quantum computation can be implemented for other quantum gate architectures, such as ion traps [14], superconducting nanocircuits [15], and semiconductor quantum dots [16]. This has made the tripod energy-level system the paradigm scenario for holonomic quantum computation.
Geometric quantum computation
Geometric quantum computation employs one-dimensional geometric phase factors instead of multidimensional holonomies to achieve universal sets of quantum gates. There are three different ways to achieve quantum computation based on geometric phases.
First, consider the Berry phase [8], which occurs in situations like the Aharonov-Bohm setup where a charged particle confined to a box acquires a geometric phase while slowly taking the box around a magnetic flux. Just as in the more general holonomies, described in the previous section, this phase arises in adiabatic evolution, but now for nondegenerate eigenspaces of Hamiltonians. In fact, the Berry phase can be thought of as an adiabatic quantum holonomy restricted to a one-dimensional energy eigenspace.
Berry phases may be used for quantum computation by encoding the logical states in nondegenerate energy levels, such as in the spin-up and spin-down states of a spin−1/2 particle in a magnetic field. When this field rotates slowly around a loop, the spin states will pick up Berry phases of magnitude given by half the enclosed solid angle and of opposite sign, which defines an adiabatic geometric phase-shift gate acting on the two spin states. But these states also pick up different dynamical phases (due to the Zeeman splitting caused by the magnetic field interacting with the spins), which one needs to compensate for. Jones et al. [12] removed these dynamical phases by a clever sequence of radio-frequency fields interrupted by suitable -pulses (which swap the spin-up and spin-down states) applied to a pair of coupled nuclear spins in an NMR setup.
The second approach to geometric quantum computation is based on the fact that geometric phases may accumulate also in nonadiabatic processes [9], as in cases where the parameters in the Hamiltonian (for instance the magnetic field in the spin-1/2 system) vary rapidly in time, causing transitions between different energy levels. These phases are determined by geometric properties of loops in the state space, such as the space representing the direction of a quantum spin, rather than loops in a space of slow parameters, such as the direction of the rotating magnetic field in the above Berry phase scenario. Compared to the Berry phase, one can identify two important advantages of nonadiabatic geometric phases: they can be implemented much faster, which means that unwanted decoherence effects have a shorter time to take effect, and they may occur even if the dynamical phases vanish, which circumvents the need to introduce complicated techniques to remove these phases.
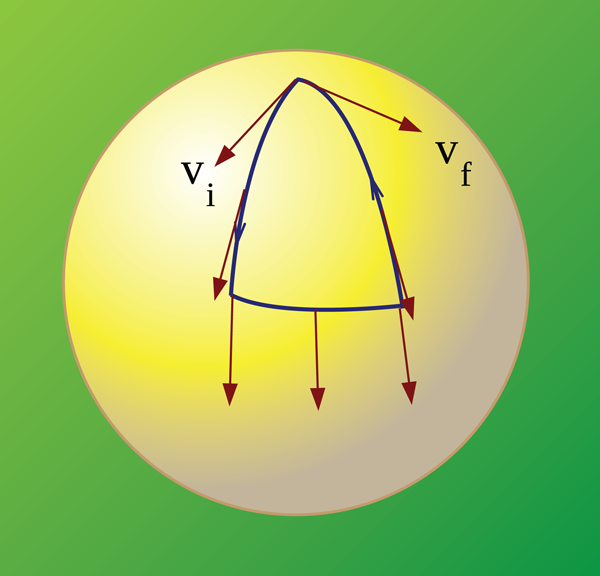
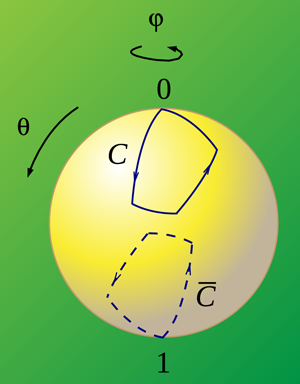
The key idea of nonadiabatic geometric quantum computation is to find paths in state space along which the dynamical phase is zero. Let us consider a single qubit whose state space is a two-dimensional sphere, called the Bloch sphere, where the polar angle (azimuthal angle ) describes the relative weight (relative phase) between the two computational basis states 0 and 1. No dynamical phases occur if we move the qubit along a great circle (geodesic) on this sphere. Now, consider evolution around a loop consisting of segments of great circles, forming a geodesic polygon (see Fig. 4). It results in a phase factor of purely geometric origin, since the dynamical phase vanishes along each geodesic segment. The geometric phase becomes half the solid angle enclosed by the loop on the Bloch sphere.
To see how nonadiabatic geometric quantum computation [17,18] can be implemented in a physical setup, one may think of a spin−1/2 particle in a magnetic field. If this magnetic field is varied so that it is always orthogonal to the evolving spin, the dynamical phase vanishes and the resulting phase becomes purely geometric. The sign of the acquired geometric phase depends on the direction of the spin, i.e., a superposition of spin-up and spin-down states picks up a relative phase that is equal to the enclosed solid angle carved out by the motion of the state vector. This phase rotation corresponds to moving the qubit state in the -direction on the Bloch sphere (see Fig. 4) and is a nonadiabatic geometric phase gate, one of the required ingredients for a universal set.
The third way to implement geometric quantum computation is based on the idea that in some cases the dynamical phase may be proportional to the geometric phase. For such evolutions, there is no need to remove the dynamical phase, as it should show the same resilience to errors as the geometric phase. This idea goes under the name unconventional geometric quantum computation [19].
As an example of this, Leibfried et al. [20] performed an experimental realization of a robust two-qubit phase gate based on an unconventional geometric phase. They demonstrated how laser beams can move two beryllium ions in space and how this motion results in a quantum phase that is conditional on the internal states of the ions. Zhu and Wang [19] subsequently proved that this phase was in fact an unconventional geometric phase being, in this case, equal to the conventional geometric phase but with a negative sign. The exceptionally high fidelity of the gate implemented by Leibfried et al. [20] indicates that unconventional geometric phase scenarios, which have also been proposed for superconducting [21] and atomic [22] qubits in cavities, could be useful for quantum computation.
Robustness
Geometric phases and quantum holonomies are global properties of quantum evolutions and are therefore robust to local errors. This is the basic reason for the conjectured resilience of holonomic and geometric quantum computation—a conjecture that has been examined in some detail recently.
To understand how geometric phase ideas can be used to achieve error resilience, consider a spin exposed to a magnetic field that fluctuates around an adiabatic loop. These fluctuations cause errors in the acquired phase of the spin. The errors reside only in the dynamical phase since the solid angle of the loop is preserved on average if the fluctuations are sufficiently random. Thus, if the dynamical phases can be removed, one can expect resilience to parameter fluctuations.
Now, the key point is that the influence of dynamical phases on quantum gates can be removed in a systematic way. There are at least two ways to do this: either use spin-echo, or encode qubit states in dark energy eigenspaces. Spin-echo is achieved by traversing the cyclic evolution twice, with the second application in the reverse direction surrounded by a pair of short -pulses that flip the qubit(s), such as in the NMR setup demonstrated by Jones et al. [12]. This results in an effective removal of the dynamical phase (including fluctuation-induced corrections) as this phase becomes an overall phase with no influence on the gate. Dark states have zero energy and therefore pick up no dynamical phase. Thus, gates based on dark states are automatically robust for adiabatic evolution—a robustness that has been confirmed in simulations of the tripod system [23]. These results constitute strong evidence for the conjectured robustness of holonomic quantum computation in the case of parameter fluctuations.
Parameter fluctuations, however, are not the only error source in quantum computation. Errors can also be introduced via environment-induced decoherence, i.e., processes where the computational system loses its coherence through entanglement with its environment. But decoherence makes it less obvious how to separate the geometric and dynamical contributions to quantum gates. These two contributions become fundamentally intertwined for decohering evolutions of quantum systems. Therefore, how the geometric phase can protect quantum information from environment-induced errors is indeed a subtle issue.
The behavior of the geometric phase in the presence of decoherence has been analyzed from different perspectives recently. Carollo et al. [24] proposed a concept of geometric phase that is based on the quantum trajectory model. This model starts from an assumption of Markovian-type evolutions, which can be decomposed into sets of trajectories of pure state evolutions. Each such quantum trajectory picks up an error-dependent geometric phase. The point with this approach is that it can be used to understand how the effect of different error sources to the geometric phase or quantum holonomy can be prevented. Using this idea, Cen and Zanardi [25] proposed a method, similar to spin-echo, to prevent dissipative errors associated with the lowest order trajectories, by traversing the trajectories twice but in the opposite direction.
Tong et al. [26] introduced a general theoretical framework to study geometric phases for nonunitary evolutions, based on quantum kinematics in interferometry. This approach catches another feature of nonunitary evolution, namely that the state of a quantum system in contact with an environment must be described by a density matrix, i.e., a statistical mixture of several wave functions. When these wave functions evolve, they acquire different geometric phases resulting in an overall geometric phase being a certain average over the statistical mixture. A key point of this approach is that it is kinematic, which means that it applies to any form of underlying dynamics. It has been used to demonstrate the existence of time [27] and temperature [28] scales on which the geometric phase is practically unaffected by decoherence and therefore useful for quantum computation.
Outlook
Advances in the field of geometric phases and quantum holonomies have led to an interesting merging of ideas in geometry and computation. We have witnessed not only new ways to implement quantum holonomies and geometric phases in real systems, but also how these implementations can be used to do robust quantum computation. The results from several groups have provided novel ideas to address the robustness of geometric phases and holonomic quantum computation.
Experiments on quantum computation using adiabatic holonomies have so far been limited to the one-dimensional case: one- and two-qubit gates implemented by geometric phases. A challenge for the future is to perform also matrix-valued holonomies in the laboratory. These are needed for all-geometric universal quantum computation and have the attractive feature of being intrinsically robust to dynamical errors. Therefore, the experimental realization of matrix-valued holonomies would be a key step towards error resilient quantum computation.
Another experimental issue worth further investigation concerns the geometric phase in the presence of open system effects. Du et al. [29] performed an NMR experiment to measure the geometric phase for mixed quantum states, theoretically proposed in [30]. Leek et al. [31] analyzed experimentally the Berry phase for a superconducting qubit affected by parameter fluctuations. A challenge for the future would be to extend this work to more general forms of open system effects, such as dissipation and quantum jumps. Such experiments would be useful to test the error resilience of holonomic and geometric quantum computation in real systems.
Research has reached a level where it becomes relevant to combine holonomic and geometric quantum computation with other forms of error-avoiding and error-correcting methods to improve error resilience. Some steps in that direction have in fact already been taken. Wu et al. [32] demonstrated how to combine the resilience of holonomic quantum computation to parameter fluctuations with the inherent robustness of decoherence free subspaces. Very recently, Oreshkov et al. [33] demonstrated how to combine holonomic quantum computation with active error correction. It seems highly desirable to develop these ideas further with the aim to find ways to reach the required precision for fault-tolerant quantum computation.
References
- P. W. Shor, inProceedings of the 35th Annual Symposium on the Foundations of Computer Science[Amazon][WorldCat] (IEEE Press, Los Alamitos, CA, 1994)
- T. Pellizzari, S. A. Gardiner, J. I. Cirac, and P. Zoller, Phys. Rev. Lett. 75, 3788 (1995)
- J. I. Cirac and P. Zoller, Phys. Rev. Lett. 74, 4091 (1995)
- A. Shnirman, G. Schön, and Z. Hermon, Phys. Rev. Lett. 79, 2371 (1997)
- D. Loss and D. P. DiVincenzo, Phys. Rev. A 57, 120 (1998)
- E. Knill, Nature 434, 39 (2005)
- F. Wilczek and A. Zee, Phys. Rev. Lett. 52, 2111 (1984)
- M. V. Berry, Proc. R. Soc. London A 392, 45 (1984)
- Y. Aharonov and J. Anandan, Phys. Rev. Lett. 58, 1593 (1987)
- P. Zanardi and M. Rasetti, Phys. Lett. A 264, 94 (1999)
- J. Pachos and S. Chountasis, Phys. Rev. A 62, 052318 (2000)
- J. A. Jones, V. Vedral, A. Ekert, and G. Castagnoli, Nature 403, 869 (2000)
- R. G. Unanyan, B. W. Shore, and K. Bergmann, Phys. Rev. A 59, 2910 (1999)
- L.-M. Duan, J. I. Cirac, and P. Zoller, Science 292, 1695 (2001)
- L. Faoro, J. Siewert, and R. Fazio, Phys. Rev. Lett. 90, 028301 (2003)
- P. Solinas, P. Zanardi, N. Zangh`ı, and F. Rossi, Phys. Rev. B 67, 121307 (2003)
- W. Xiang-Bin and M. Keiji, Phys. Rev. Lett. 87, 097901 (2001)
- S.-L. Zhu and Z. D. Wang, Phys. Rev. Lett. 89, 097902 (2002)
- S.-L. Zhu and Z. D. Wang, Phys. Rev. Lett. 91, 187902 (2003)
- D. Leibfried, B. DeMarco, V. Meyer, D. Lucas, M. Barrett, J. Britton, W. M. Itano, B. Jelenkovic, C. Langer, T. Rosenband, and D. J. Wineland, Nature 422, 412 (2003)
- S.-L. Zhu, Z. D. Wang, and P. Zanardi, Phys. Rev. Lett. 94, 100502 (2005)
- C. Y. Chen, X.-L. Zhang, Z. J. Deng, K.-L. Gao, and M. Feng, Phys. Rev. A 74, 032328 (2006)
- P. Solinas, P. Zanardi, and N. Zangh`ı, Phys. Rev. A 70, 042316 (2004)
- A. Carollo, I. Fuentes-Guridi, M. Franca Santos, and V. Vedral, Phys. Rev. Lett. 90, 160402 (2003)
- L.-X. Cen and P. Zanardi, Phys. Rev. A 70, 052323 (2004)
- D. M. Tong, E. Sjöqvist, L. C. Kwek, and C. H. Oh, Phys. Rev. Lett. 93, 080405 (2004)
- F. C. Lombardo and P. I. Villar, Phys. Rev. A 74, 042311 (2006)
- A. T. Rezakhani and P. Zanardi, Phys. Rev. A 73, 052117 (2006)
- J. F. Du, P. Zou, L. C. Kwek, J.-W. Pan, C. H. Oh, A. Ekert, D. K. L. Oi, and M. Ericsson, Phys. Rev. Lett. 91, 100403 (2003)
- E. Sjöqvist, A. K. Pati, A. Ekert, J. S. Anandan, M. Ericsson, D. K. L. Oi, and V. Vedral, Phys. Rev. Lett. 85, 2845 (2000)
- P. J. Leek, J. M. Fink, A. Blais, R. Bianchetti, M. G¨oppl, J. M. Gambetta, D. I. Schuster, L. Frunzio, R. J. Schoelkopf, and A. Wallraff, Science 318, 1889 (2008)
- L.-A. Wu, P. Zanardi, and D. A. Lidar, Phys. Rev. Lett. 95, 130501 (2005)
- O. Oreshkov, T. A. Brun, and D. A. Lidar, arXiv:0806.0875
- J.-S. Tsai and Y. Nakamura, NEC Research, http://www.nec.co.jp/rd/Eng/innovative/E3/top.html