High-energy physics in a new guise

Marcel Franz

Viewpoint

High-energy physics in a new guise

Department of Physics and Astronomy, University of British Columbia, Vancouver, BC, Canada V6T 1Z1

November 24, 2008• Physics 1, 36

The esoteric concept of “axions” was born thirty years ago as an attempt to resolve a puzzle in the description of the strong interaction between quarks. It appears that the same physics—though in a much different context—applies to an unusual class of insulators.

Figure caption — **Figure 1:** A magnetoelectric effect in a topological insulator. (Left) A quantum Hall effect occurs without strong magnetic field when an electric field applied in the plane of the interface between a topological (red region) and an ordinary (blue region) insulator (or vacuum) induces a precisely quantized current perpendicular to the field. (Right) A magnetic field applied perpendicular to the same interface introduces $(n + 1 / 2)$ electrons for each flux quantum of applied field. The shaded region corresponds to the charge density, $ρ$ , of the electrons, which mainly concentrates around the boundary between the two insulators and is largest where the magnetic field is strongest.

In a prescient but until recently largely forgotten 1987 paper, Frank Wilczek [1] analyzed the effect of hypothetical elementary particles called “axions” on the laws of electricity and magnetism. Axions had been postulated in 1977 in an attempt to explain the absence of charge-parity (CP) violation in the strong interaction between quarks. Wilczek showed that the electrodynamics of axions can be described if one adds a term of the form $Δ L_{a x i o n} = θ (e^{2} / 2 π h c) B \cdot E$ to the ordinary Maxwell Lagrangian that governs the behavior of the electromagnetic field, where $θ$ describes the strength of the axion field. Such a term is allowed by symmetry, but causes nontrivial modifications to Maxwell’s equations.

As far as we know today, axions do not occur in empty space, and the electrodynamics of these particles appeared to have gone down in history as an interesting curiosity, not relevant to the universe we live in. In a paper appearing in Physical Review B, however, Xiao-Liang Qi, Tayor Hughes, and Shou-Cheng Zhang of Stanford University [2] show that a term $Δ L_{a x i o n}$ , analogous to what was predicted in high-energy physics, is present in the theoretical description of a class of crystalline solids called topological insulators. The existence of topological insulators—materials characterized by a bulk energy gap and the presence of conducting surface states that are robust (or “topologically protected”) to impurities and defects—had been predicted in a series of recent theoretical works [3–5] and was confirmed experimentally this year in the semiconducting alloy ${Bi}_{1 - x} {Sb}_{x}$ by a group at Princeton [6]. All of these developments have propelled axion electrodynamics from an idle curiosity to an experimentally observable reality. Aside from establishing the axion term, Qi et al. [2] provide a number of important insights into the physics of topological insulators and make connections with other known topological states of matter, notably the quantum Hall liquids.

Wilczek showed that the axion term has two important consequences: it modifies Gauss’ law by adding to the source term an extra charge density, so that $\nabla \cdot E = ρ$ becomes $\nabla \cdot E = ρ - (e^{2} / 2 π h c) \nabla θ \cdot B$ , and revises Ampère’s law by contributing an additional current density, so that $\nabla \times B = \partial_{t} E + j$ becomes $\nabla \times B = \partial_{t} E + j + (e^{2} / 2 π h c) (\nabla θ \times E + \partial_{t} θ B)$ .

The extra charge and current density only appear when the quantity $θ$ varies in space or time. Of course, $θ$ in crystalline solids describes something much different than the original “axions” that were hypothesized in high-energy physics. The Stanford group show that, provided the electrons’ equations of motion are time-reversal invariant, all three-dimensional insulating solids can be characterized by a quantized value of the axion field in their bulk: $θ = 2 π n$ , with $n$ integer in ordinary insulators, while $θ = 2 π (n + 1 / 2)$ in topological insulators. It follows then that $θ$ must vary near any boundary between two insulators characterized by different bulk values of $θ$ , and the effects of axion electrodynamics should become apparent in that region of space.

There is an important subtlety in the above classification of time-reversal invariant insulators. It turns out that while the boundary between either two ordinary or two topological insulators does not necessarily exhibit interesting behavior vis-à-vis axion electrodynamics, the boundary between a topological insulator and an ordinary insulator (or the vacuum, which presumably has $θ = 0$ ) is a very special place where Maxwell laws do not hold in their conventional form.

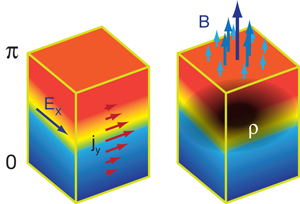
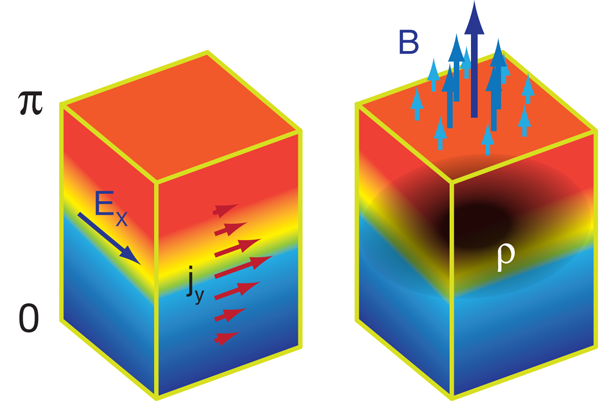
The modifications to Maxwell’s equations give rise to some very interesting phenomena illustrated in Fig. 1. Perhaps the most remarkable of these is the finding that the boundary between a topological insulator and a normal insulator exhibits a quantum Hall effect: when an electric field $E$ is applied in the plane of the boundary, a current flows in the direction perpendicular to $E$ (Fig. 1, left). This is a direct consequence of the modification to Ampère’s law. This Hall current is dissipationless, a property that could be potentially useful in future electronic devices. The magnitude of the current is given by $σ_{H} E$ with the “Hall” conductance quantized as $σ_{H} = (e^{2} / h) (n + 1 / 2)$ . The factor of 1/2 means that the surface exhibits a fractional quantum Hall effect. It is also notable that, unlike what is found in two-dimensional electron gasses, the Hall effect occurs here in the absence of a strong external magnetic field (although a weak magnetic field, or another time-reversal breaking perturbation is needed to determine the direction of the Hall current [1,2]).

Similarly, according to the modified Gauss’ law, a magnetic field applied perpendicular to the plane of the surface leads to accumulation of charge (Fig. 1, right). The total accumulated charge corresponds to $e (n + 1 / 2)$ per flux quantum of the applied field. Thus, interestingly, one can think of a fractional charge, equal to a half-integer number of electrons, as being bound to each flux quantum. In this context, one can hypothesize that, in analogy with the fractional quantum Hall states, these flux-charge composites will exhibit fractional exchange statistics and thus be potentially useful in schemes that seek to implement fault-tolerant quantum computation [7,8]. Finally, the surface of a topological insulator can rotate the polarization vector of reflected light (Kerr effect) and would be another experimental signature of axion electrodynamics in these materials.

What is the microscopic picture for these effects? The key ingredient is the presence of strong spin-orbit coupling, which typically occurs in crystalline solids that are made from the heavier elements, such as $Pb$ and $Bi$ . Under the right conditions, the spin-orbit terms can give rise to anomalous band structure that can in turn support topologically robust gapless states at the surfaces of a bulk insulator. This means that bands associated with the surface states are guaranteed to meet at a certain number of points in the surface Brillouin zone, while the bulk bands remain separated by a gap. These surface states are chiral—specifically, the electron spin and momentum are aligned—and at low energies resemble states of massless Dirac fermions, now familiar from the physics of graphene.

The precise definition of the topological insulator involves counting these surface states: an odd number corresponds to a topological insulator, whereas an even number implies ordinariness [3,4]. That number $N$ is also related to $θ$ from the above discussion of axion electrodynamics. Specifically, it holds that $N = θ / π$ . Remarkably, whether $N$ is odd or even depends only on the bulk properties of the insulator. This situation is reminiscent of the integer quantum Hall systems where the number of chiral edge states is determined by the bulk Hall conductance. In fact, Qi et al. make this connection more transparent by deriving the topological invariant of a three-dimensional insulator from the fictitious four-dimensional quantum Hall system employing an ingenious procedure of dimensional reduction.

Having an odd number of chiral Dirac fermions at a surface is itself odd. In fact, the famous Nielsen-Ninomyia “no-go” theorem [9] states that under very general conditions such Dirac fermions must always come in pairs of opposite chirality, e.g., as they do in graphene. A topological insulator evades this theorem by spatially separating the states of opposite chirality so that they appear on its opposite surfaces. In this way the three-dimensional system as a whole satisfies the no-go theorem but its surfaces, when viewed in isolation, seemingly violate it. Qi et al. explain how the axion phenomenology discussed above arises at the microscopic level from the odd number of topologically robust chiral surface states.

The anomalous surface states that are characteristic of topological insulators have other possible applications that go beyond axion electrodynamics. An example is the proposal put forward by Fu and Kane [10] to pair the surface electrons of a topological insulator into a superconducting state by means of the proximity effect. Owing to the chiral nature of the surface electrons, this superconducting state has unusual topological excitations, with just the right properties to be potential fundamental blocks for quantum computers [7].

The unusual phenomenology of topological insulators arises from the interplay between their unique band structure and the well understood physics of spin-orbit coupling. Thus, remarkably, these systems can be thought of as weakly interacting in the sense that electron-electron interactions play no significant role. Ever since Anderson’s famous 1972 essay “More is different” [11], no condensed-matter physicist has doubted the virtually limitless potential for discovery of new phenomena in interacting quantum many-body systems. That something radically new can appear even in noninteracting systems came both as a great surprise and a promise that profound discoveries can be made where no one expects them.

References

F. Wilczek, Phys. Rev. Lett. 58, 1799 (1987)
X-L. Qi, T. L. Hughes, and S-C. Zhang, Phys. Rev. B 78, 195424 (2008)
L. Fu, C. L. Kane, and E. J. Mele, Phys. Rev. Lett. 98, 106803 (2007)
J. E. Moore and L. Balents, Phys. Rev. B 75, 121306 (2007)
R. Roy, arXiv:cond-mat/0607531
D. Hsieh, D. Qian, L. Wray, Y. Xia, Y. S. Hor, R. J. Cava, and M. Z. Hasan, Nature 452, 970 (2008)
A. Y. Kitaev, Ann. Phys. 303, 2 (2003)
C. Weeks, G. Rosenberg, B. Seradjeh, and M. Franz, Nature Phys. 3, 796 (2007)
H. B. Nielsen and M. Ninomiya, Phys. Lett. 105B, 219 (1981)
L. Fu and C. L. Kane, Phys. Rev. Lett. 100, 096407 (2008)
P. W. Anderson, Science 177, 393 (1972)

About the Author

Marcel Franz studied physics as an undergraduate at the Comenius University in Bratislava, Czechoslovakia, and received his Ph.D. from the University of Rochester in 1994. After postdoctoral appointments at McMaster and Johns Hopkins Universities, he was appointed Assistant Professor (2000), and later Associate Professor (2006) at the University of British Columbia. He received the A. P. Sloan Fellowship (2004), and become a member of the Canadian Institute for Advanced Research (2003). His main research interests include superconductivity, strongly correlated electron systems, and all things unusual. He also likes to spend time at the Aspen Center for Physics and the Kavli Institute for Theoretical Physics (KITP) in Santa Barbara.