The many shapes of spinning drops
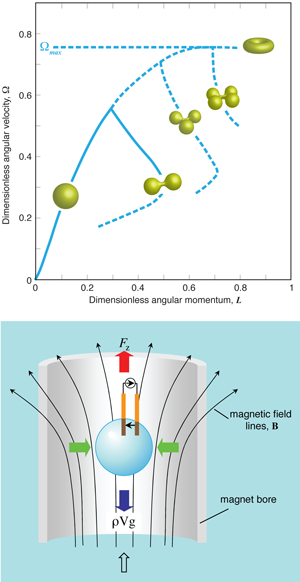
Liquids, such as water or oil, can form droplets that are held together by surface tension—a cohesive force that causes the surface of many liquids to behave as an elastic membrane. Because liquid droplets are fairly simple to study and control under different conditions, they have fascinated experimentalists and theoreticians—including Laplace, Gauss, Poincarè, Chandrasekhar, Bohr, and Wheeler—for more than two centuries. A droplet on a surface, for example, spreads out or balls up depending on its interaction with the surface. But what happens to the shape of droplets in motion? As a freely suspended droplet rotates at higher and higher velocity, the droplet will tend to get pulled apart and deform. Droplets distort according to a minimum energy principle, always seeking the lowest energy state for a given rotational frequency, and theorists predicted that they would form the series of equilibrium shapes shown in the top of Fig. 1 [1].
To see the full range of shapes shown in Fig. 1 requires a carefully designed experiment. First, the effects of gravity must be removed, since the theoretical predictions assume a freely suspended droplet. Second, the viscous drag on the droplet must be as small as possible. Finally, the droplets must spin at a controllable rate. Writing in Physical Review Letters, Richard Hill and Laurence Eaves of the University of Nottingham in the UK have been able to achieve this by ingeniously combining diamagnetic levitation of water droplets in air with a liquid electric motor technique to spin up the droplets [2]. They are able to observe several different families of rotating water droplets, compare with theoretical expectations, and even record the centimeter-sized droplets in several movies. Because liquid drop models are used to describe systems like atomic nuclei and black holes that cannot be controlled in the laboratory, their work opens the way to a whole new series of measurements of direct interest to several branches of physics.
The first experimental investigations of rotating fluid droplets were conducted by a blind Belgian physicist named Joseph-Antoine-Ferdinand Plateau [3] (Plateau, who also performed experiments with light, once kept his naked eyes fixed for too long on the sun, which brought on a choroid inflammation and total blindness in 1843). Plateau suspended olive oil in a mixture of water and alcohol that had the same density as the oil, thereby balancing gravity with the buoyant force and leaving the droplet effectively weightless. Starting with a nonrotating drop of spherical shape, Plateau found that as he rotated the droplet at higher and higher speeds, the droplet transformed from a spherical shape (at zero rotation), to axisymmetric shapes (at slow speeds), to ellipsoidal and 2-lobed “peanut” shapes, and finally a toroidal shape at very large rotational speeds. These are the same shapes shown in Fig. 1, which were fully understood theoretically about 100 years after Plateau’s experiments.
Unfortunately, in Plateau’s setup the surrounding fluid exerted a large viscous drag on the rotating droplets, which induced unwanted shape deformations. The droplets were also hard to control and to spin, therefore comparisons with theoretical results were mainly qualitative. More recently, precise experiments with silicone oil droplets have been performed in orbiting spacecraft [4], and it has been possible to see the 2-lobed droplet shape. Unfortunately, special care is needed to control and spin up the droplet using acoustic pressure waves, not to mention that it requires going into space!
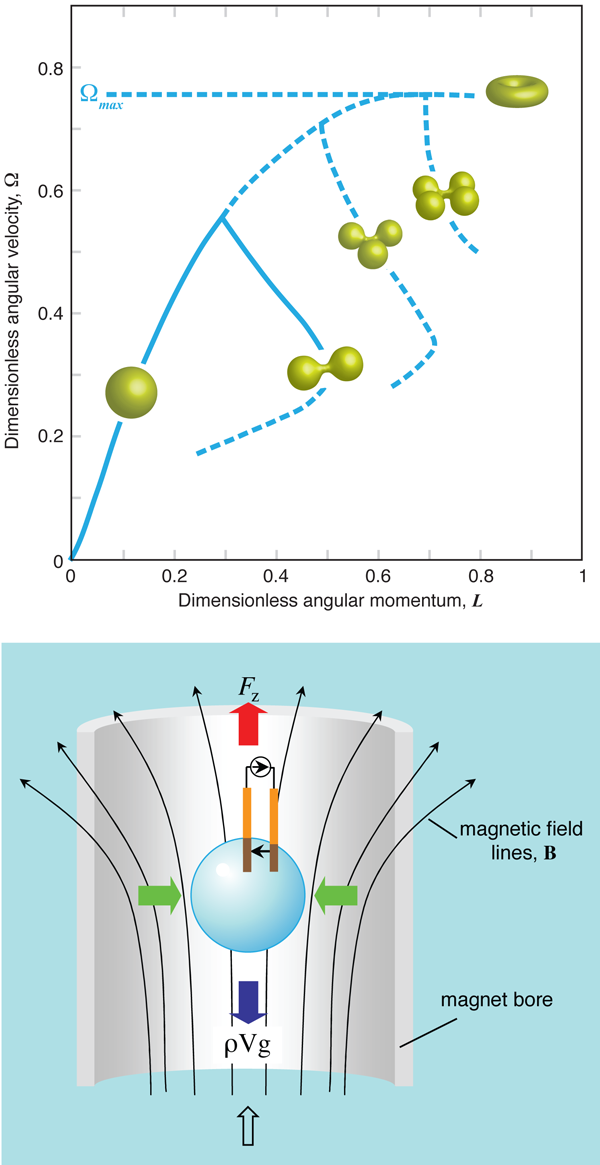
Hill and Eaves found an innovative way to compensate for the effects of gravity and to make the droplets spin. They solved the gravity problem by using diamagnetic levitation (Fig. 1, bottom). Many substances, including water, are diamagnetic. When acted upon by external magnetic fields, the electrons in diamagnetic materials rearrange themselves creating small currents, which oppose the external field. In a magnetic field that is not constant in space, a diamagnet will always seek the lower field strength. Thus, diamagnetic substances, despite being weakly magnetic, can easily be levitated if the exterior magnetic field has high enough intensity and a well-defined gradient (in fact, even animals, such as frogs, can be levitated diamagnetically [5]).
To set the droplet into rotation, the Nottingham group designed a “liquid electric motor,” also shown in the bottom part of Fig. 1. They inserted two thin wire electrodes in the droplet, with one wire aligned with the droplet center and with the magnetic field. The other wire was set parallel to the first a distance away. A current was set to flow through these wires. It follows that a Lorentz force acts on the droplet, causing a torque of on the droplet that accelerates it to rotate around the vertical axis with a frequency that can be easily controlled by adjusting the current.
There is one final catch to the experiment: the off-axis electrode can excite small amplitude waves on the surface of the droplet, like a boat moving on a water surface. These excited waves have an important effect, in that they can help stabilize otherwise unstable configurations [6]. For instance, 3-lobed configurations cannot usually be observed since they are unstable and rapidly decay into another configuration (typically the 2-lobed shapes). However, if the small waves excited by the off-axis electrode are in resonance with this configuration, they are able to sustain 3-lobed configurations far longer than expected. As the rotation of the droplet increases, it progresses through an elliptical (not shown in Fig. 1) and then a 2-lobed shape. As the rotation increases even further, the droplet assumes a 3-lobed configuration, which was measured accurately for the first time in this experiment. It turns out that the critical rotational frequency at which 2 and 3-lobed shapes start to develop agrees very well with theoretical predictions (see Video 1 and 2). A sequence of beautiful movies of this experiment can be seen at http://netserver.aip.org/cgi-bin/epaps?ID=E-PRLTAO-101-065848).
Attempts to understand rotating fluid droplets have been more than an academic exercise. Since surface tension is a cohesive force, it can be used to model other cohesive forces, such as gravity, that hold together stars and planets, and the nuclear interactions that hold together nuclei [7,8]. Higher dimensional objects (that is, objects which only exist in a large number of space-time dimensions) with an event horizon seem to behave in general as fluid membranes [7,9]. Recently, the breakup of extended black-hole-like objects that are called “black strings” was explained in terms of the same classical fluid mechanics instability that is responsible for the breakup of fluid jets in a water tap, or for the formation of water droplets in rain [7,10]. Simultaneously, it has been understood that many field theories have a hydrodynamic description in the limit of high energy density [11]. If we combine this description with the now famous gravity/quantum field duality [12], we are left with a gravity/hydrodynamic duality, where fluids are literally dual to black holes [13]. Therefore droplets, fluid cylinders, and other fluid configurations could teach us how gravity behaves, with the experimental solution of Hill and Eaves providing a simple way to investigate these exciting issues in table-top experiments.
Acknowledgments
This work is supported by Fundação para a Ciência e Tecnologia (FCT) - Portugal through project PTDC/FIS/64175/2006 and by a Fulbright Scholarship. I thank E. Berti, M. Casals, Ó. Dias, M. Lemos, P. Pani, J. Rocha, P. Ricarte, A. Sousa, U. Sperhake, and H. Witek for a careful reading of the manuscript and useful comments.
References
- R. A. Brown and L. E. Scriven, Proc. R. Soc. London A 371, 331 (1980)
- R. J. A. Hill and L. Eaves, Phys. Rev. Lett. 101, 234501 (2008)
- J. Plateau, Statique Expérimentale et Théorique des Liquides Soumis aux Seules Forces Moléculaires, (Paris, Gauthier-Villars, 1873).
- C. P. Lee, A. V. Anilkumar, A. B. Hmelo, and T. G. Wang, J. Fluid Mech. 354, 43 (1998)
- http://www.hfml.ru.nl/froglev.html
- K. Ohsaka and E. H. Trinh, Phys. Rev. Lett. 84, 1700 (2000)
- V. Cardoso and Ó. J. C. Dias, Phys. Rev. Lett. 96, 181601 (2006); V. Cardoso and L. Gualtieri, Class. Quantum Grav. 23, 7151 (2006)
- N. Bohr and J. A. Wheeler, Phys. Rev. 56, 426 (1939); C. Wong, Ann. Phys. 77, 279 (1973)
- K. S. Thorne, D. A. MacDonald, and R. H. Price, Black Holes: The Membrane Paradigm (Yale University Press, 1986)
- M. M. Caldarelli, O. J. C. Dias, R. Emparan, and D. Klemm, arXiv:0811.2381
- P. Kovtun, D. T. Son, and A. O. Starinets, Phys. Rev. Lett. 94, 111601 (2005); J. High Energy Phys. 0310, 064 (2003)
- J. M. Maldacena, Adv. Theor. Math. Phys. 2, 231 (1998)
- S. Bhattacharyya et al., J. High Energy Phys. 0806, 055 (2008)