Topological states of quantum matter

Shou-cheng Zhang

Viewpoint

Topological states of quantum matter

Department of Physics, Stanford University, Stanford, CA 94305-4045 USA

July 23, 2008• Physics 1, 6

Electrons in graphene can be described by the relativistic Dirac equation for massless fermions and exhibit a host of unusual properties. The surfaces of certain band insulators—called topological insulators—can be described in a similar way, leading to an exotic metallic surface on an otherwise ‘ordinary’ insulator.

Figure caption — **Figure 1:** When we think of topology, we normally think of objects that cannot be simply transformed into each other, such as a rubber band and a Möbius strip (top). The metallic surface of a topological insulator is different from an ordinary surface because its metallic nature is protected by certain symmetry invariants. In this sense, it cannot be simply transformed into the surface of a normal insulator. The sketches (bottom) show the electronic structure (energy versus momentum) for a “trivial” insulator (left) and a strong topological insulator (right), such as ${Bi}_{1 - x} {Sb}_{x}$ . In both cases, there are allowed electron states (black lines) introduced by the surface that lie in the bulk band gap (the bulk valence and conduction bands are indicated by the green and blue lines, respectively). In the trivial case, even a small perturbation (say, changing the chemistry of the surface) can open a gap in the surface states, but in the nontrivial case, the conducting surface states are protected. Note that in the topological insulator, the surface states are linear in momentum and meet at an odd number of points in $k$ -space.

Most quantum states of matter are categorized by the symmetries they break. For example, the crystallization of water into ice breaks translational symmetry or the magnetic ordering of spins breaks rotational symmetry. However, the discovery in the early 1980s of the integer and fractional quantum Hall effects has taught us that there is a new organizational principle of quantum matter. In the quantum Hall state, an external magnetic field perpendicular to a two-dimensional electron gas causes the electrons to circulate in quantized orbits. The “bulk” of the electron gas is an insulator, but along its edge, electrons circulate in a direction that depends on the orientation of the magnetic field. The circulating edge states of the quantum Hall state are different from ordinary states of matter because they persist even in the presence of impurities. The reason for this is best expressed mathematically (it is related to the quantization of Berry’s phases, see, for example, Physics Today August 2003 [1]), and is not intuitively obvious, but the effect—circulating current—is real and measurable.

In the last few years, a number of theorists realized that the same “robust” conducting edge states that are found in the quantum Hall state could be found on the boundary of two-dimensional band insulators with large spin-orbit effect, called topological insulators. In these insulators, spin-orbit effects take the role of an external magnetic field, with spins of opposite sign counter-propagating along the edge [2-5]. In 2006, my colleagues and I predicted this effect (later confirmed) on the edge of $HgTe$ quantum wells [2,3]—the first experimentally realized quantum spin Hall state. In 2007 Liang Fu and Charles Kane of the University of Pennsylvania predicted that a three-dimensional form of the topological insulator with conducting surface states could exist in ${Bi}_{1 - x} {Sb}_{x}$ , an alloy in which spin-orbit effects are large [6]. Earlier this year, photoemission measurements of the surface of ${Bi}_{1 - x} {Sb}_{x}$ supported this picture [7], strongly suggesting that ${Bi}_{1 - x} {Sb}_{x}$ is the first realization of a topological insulator in three dimensions and that its surface is a topological metal in two dimensions. Now, in an article appearing in the current issue of Physical Review B [8], the same authors and Jeffrey Teo present a detailed calculation of the electronic structure of the surface states in this material that can be directly tested in future experiments.

To understand why the surface of ${Bi}_{1 - x} {Sb}_{x}$ is exotic, it helps to think about what a surface is like in a “normal” insulator. Recall that the surface and bulk states of electrons inside crystalline solids are described by wave functions obtained from solving Schrödinger’s equation. This quantum mechanical framework predicts that there are gaps in the electronic energy spectrum where no wave solutions are possible inside the bulk crystal. If the Fermi level lies inside this energy gap (or “band gap”), the solid is insulating. However, dangling bonds or a reorganization of atoms on the surface can introduce states that have energies that lie within the forbidden energy gap, but are restricted to move around the two-dimensional surface. In most situations these conducting surface states are very fragile and their existence depends on the details of the surface geometry and chemistry. In contrast, in a topological insulator, these surface states are protected, that is, their existence does not depend on how the surface is cut or distorted. Again, the reason for this is, at its root, mathematical, and lies in the fact that the Hamiltonian describing the surface states is invariant to small perturbations.

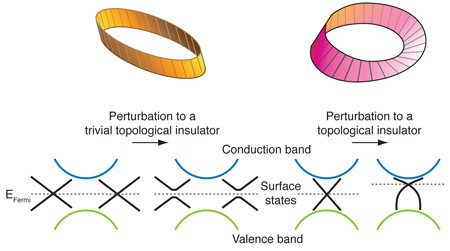
The concept of a topological insulator is perhaps confusing, because when we think of two objects as topologically distinct, we imagine the difference between say, a Möbius strip and a rubber band (Fig. 1). We can’t deform one into the other. The same is true for the Hamiltonian that describes a topological insulator: the Hamiltonian permits conducting states that circulate along the edge (in a two-dimensional insulator) or the surface (in the three-dimensional case) and no simple deformation to the edge (or surface) can destroy these conducting states. Moreover, the conducting states are real and can be measured, and in the case of the quantum spin Hall state, are naturally spin polarized, which can have interesting applications in spintronics.

What’s special about the surface of ${Bi}_{1 - x} {Sb}_{x}$ that it has these properties? It turns out that the surface states of this alloy are similar to the two-dimensional states in graphene. Near the Fermi level, electrons and holes in graphene are described by energy states that are linear in momentum. Electrons with a constant velocity are conveniently described by the relativistic Dirac equation for massless fermions. (The electrons in graphene are not actually massless; the linear bands result from the atomic structure of this two-dimensional system.) In two-dimensional k-space, the dispersion relation looks like two cones that meet at discrete (Dirac) points at the Fermi level. However, while graphene has an even number of Dirac points at the Fermi level, ${Bi}_{1 - x} {Sb}_{x}$ has an odd number. Kramers theorem tells us that the degeneracy of states with an even number of electrons that obeys time reversal symmetry will always be lifted. For this reason, the surface states in graphene are easily destroyed because a gap will open (they are “topologically trivial”) while the surface states of ${Bi}_{1 - x} {Sb}_{x}$ are said to be “topologically protected” (see Fig. 1). In fact, in graphene, if one distorts the energies of the two carbon atoms in one unit cell relative to each other, the Dirac points disappear immediately. In contrast, the massless Dirac states on the surface of ${Bi}_{1 - x} {Sb}_{x}$ are robust, even if the surface itself is slightly imperfect or possesses impurities.

In their paper, Teo et al. use a tight-binding model (a well-established method for determining the band structure in an insulator) that they solve numerically to determine the electronic structure on a particular ${Bi}_{1 - x} {Sb}_{x}$ surface. The model reproduces the surface structure of ${Bi}_{1 - x} {Sb}_{x}$ and the authors can determine which surfaces will behave as topological metals. However, the paper also makes general symmetry arguments that are model independent that could potentially be applied to determine if other materials are good candidates for topological insulators.

Topological quantum states of matter are very rare and until recently the quantum Hall state provided the only experimentally realized example. The application of topology to physics is an exciting new direction that was first initiated in particle physics and quantum field theory. However, there are only a few topological effects that have been experimentally tested in particle physics. Topological states of quantum matter now offer a new laboratory to test some of the most profound ideas in mathematics and physics. In 2007, the theoretical prediction and experimental observation of the quantum spin Hall state—a topological insulator in two dimensions—in $HgTe$ quantum wells was highlighted as one of the top ten breakthroughs among all sciences [2,3,9].

Topological states of quantum matter are generally described by topological field theories. Readers may already be familiar with Maxwell’s field theory describing the electromagnetic fields and Einstein’s field theory describing the gravitational fields. These field theories depend on the geometry of the underlying space. In contrast, topological field theories do not depend on the geometry, but only on the topology of the underlying space.

One of the most striking predictions of topological field theory is the so-called topological magnetoelectric effect, where an electric field induces a magnetic field along the same direction inside a topological insulator, with a constant of proportionality given by odd multiples of the fine structure constant [13]. Such a prediction can be readily tested in ${Bi}_{1 - x} {Sb}_{x}$ . Although the tight-binding model that the authors use to calculate the electronic band structure for ${Bi}_{1 - x} {Sb}_{x}$ is more complicated that that for $HgTe$ , and there are some quantitative disagreements with the first principle calculations, its essential properties can be understood with a simple topological field theory.

Now that two topological states of quantum matter have been experimentally discovered—the quantum Hall and the quantum spin Hall states—one may naturally wonder about how they would fit into a bigger unifying picture. For example, the periodic table gives an organizational principle of all elements, and symmetry principles fit all elementary particles into their right places. The paper from the Kane group suggests that what we know about topological insulators may be just the tip of the iceberg and that other classification schemes exist as well. Once we discover the deeper organizational principle of topological states of quantum matter, we may be able to predict many more, each with its own unique and beautiful properties.

References

J. E. Avron, D. Osadchy, and R. Seiler, Phys. Today 56, 38 (2003)
B. A. Bernevig, T. L. Hughes, and S.-C. Zhang, Science 314, 1757 (2006)
M. Konig, S. Wiedmann, C. Brune, A. Roth, H. Buhmann, L. W. Molenkamp, X.-L. Qi, and S.-C. Zhang, Science 318, 766 (2007)
C. L. Kane and E. J. Mele, Phys. Rev. Lett. 95, 146802 (2005)
B. A. Bernevig and S-C. Zhang, Phys. Rev. Lett. 96, 106802 (2006)
L. Fu and C. L. Kane, Phys. Rev. B 76, 045302 (2007)
D. Hsieh, D. Qian, L. Wray, Y. Xia, Y. S. Hor, R. J. Cava, and M. Z. Hasan, Nature 452, 970 (2008)
J. C. Teo, L. Fu and C. L. Kane, Phys. Rev. B 78, 045426 (2008)
E. Kintisch and R. A. Kerr, Science 318, 1846 (2007)
L. Fu, C. L. Kane and E. J. Mele, Phys. Rev. Lett. 98, 106803 (2007)
J. E. Moore and L. Balents, Phys. Rev. B 75, 121306 (2007)
R. Roy, arXiv:cond-mat/0604211v2
X. L. Qi, T. Hughes, and S.-C. Zhang, arXiv:0802.3537

About the Author

Shou-cheng Zhang received his B.Sc. in physics (1983) from the Free University of Berlin in Germany and his Ph.D. degree in physics (1987) from the State University of New York at Stony Brook. He subsequently held a postdoctoral fellowship at the Institute for Theoretical Physics at Santa Barbara (1987–1989) and a staff position at IBM Almaden Research Center (1989–1993). Since 1993 he has been a Professor of Physics at Stanford University. He also holds an appointment in the Applied Physics and Electrical Engineering Departments and is currently the co-director of the Stanford Center for Spintronics Science and Application. His research interests lie in the areas of quantum spin transport, the quantum spin Hall effect and the theory of high-temperature superconductivity.