A Superconducting Qubit that Protects Itself
Today, noise poses one of the biggest challenges for quantum computation efforts. Be it in the form of dissipated heat, electromagnetic radiation, or something else, noise can disrupt fragile quantum superpositions and lead to errors. The jury is still out on which approach will be most successful in protecting quantum information against noise, but the hope clearly lies in quantum error correction (QEC) protocols. Now, Martin Rymarz of RWTH Aachen University in Germany and colleagues have proposed a novel superconducting circuit implementation that realizes a QEC strategy in which robustness against noise is an intrinsic feature of the hardware [1]. This strategy, known as the Gottesman-Kitaev-Preskill (GKP) code, was proposed in 2001 [2]. However, implementing it with superconducting circuits has so far been impossible because it requires a large magnetic field. The newly proposed architecture circumvents this obstacle by employing a synthetic magnetic field, pushing the GKP protocol closer to a possible realization.
The noise processes that threaten quantum computing are assumed to be local, meaning that they act on specific parts of circuits, such as individual physical qubits. In the “scaling-up” approach to QEC, quantum information is encoded into multiple physical qubits that form each logical qubit used for the actual computation tasks. So even if one physical qubit is disrupted by noise, the information carried by the logical qubit will not be corrupted. In the “exotic-state” approach to QEC, each computational unit is a single oscillator, and the logical bits are represented by two special states of the oscillator, called nontrivial states, that are robust against local noise. The exotic-state technique employs continuous-variable systems, such as electromagnetic modes, which are initialized in states that are either robust by themselves (passive QEC) or can be stabilized via operations that do not affect the logical qubit (active QEC).
The GKP strategy is one example of the exotic-state approach [2]. In the GKP code, the exotic states are called grid states, which are superpositions of an oscillator’s position eigenstates [2]. The robustness to noise in an active GKP protocol stems from the fact that small shifts in the momentum and position of the oscillator can be identified and corrected before they can corrupt the logical information. An experimental demonstration of grid states was recently realized in a superconducting circuit architecture with an active QEC protocol [3]. A GKP code with passive QEC, however, has not yet been demonstrated. Compared to active QEC, which requires complicated operations for error recovery, a passive QEC approach promises to be more efficient and could be advantageous for scaling up to larger computing architectures, as it requires fewer physical units.
A prototypical implementation of a passive GKP code involves an electron confined to two dimensions in a large magnetic field. Realizing such a passive GKP-code design with superconducting circuit architectures is not straightforward. The design would require a magnetic field to interact with microwave photons, which are the oscillations of the electromagnetic field in the superconducting circuit. But photons are neutral particles and do not interact with magnetic fields in the same way that charged particles, such as electrons, do. Strategies for creating artificial magnetic fields that can interact with photons have been discussed and demonstrated in some superconducting systems [4–6]. The role of magnetic fields, whether real or artificial, in these systems is to break time-reversal symmetry, creating “nonreciprocal” circuits with multiple ports. The nonreciprocity means that the circuits process photons in a different way depending on which port they are injected into. This asymmetry can be exploited to build nonreciprocal devices that transmit microwave signals in one direction while blocking them in the reverse direction [6].
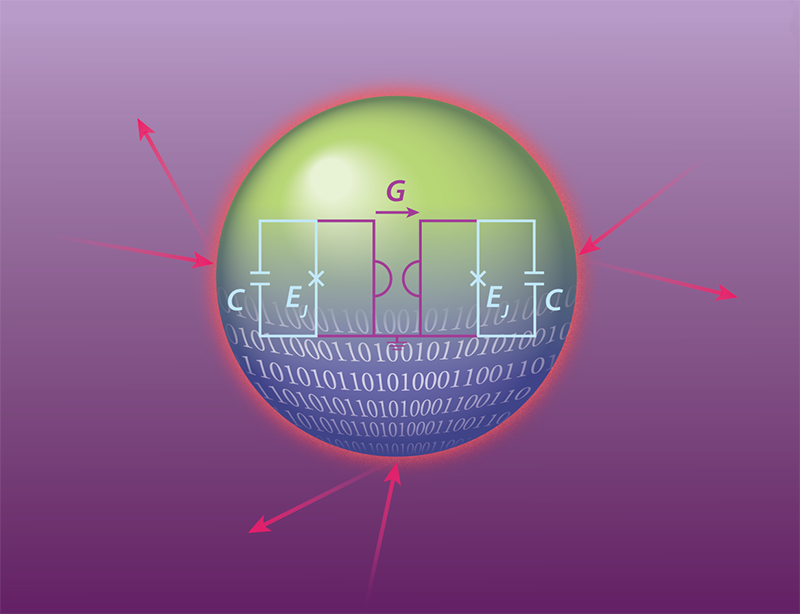
Rymarz and colleagues have proposed a way of utilizing synthetic magnetic fields, allowing for a superconducting qubit realization of the GKP code. They propose a system in which two superconducting anharmonic oscillators, called fluxonium circuits, are coupled via a gyrator, a device that can invert the current-voltage characteristics of a circuit element (Fig. 1). The asymmetric response of the gyrator implies a breaking of time-reversal symmetry like that produced by a magnetic field. The team shows that the ground states of the system correspond to the GKP “code words”—the grid states that are used to encode the logical information. The huge advantage here is that the logical qubit is constructed from the ground states of the system—in which the system will reside if no external energy is supplied. Leaving the ground state would corrupt the logical qubit, but it comes with an energy penalty, so the protection is naturally built in.
The researchers show that the proposed superconducting circuit simulates the model of an electron confined to a two-dimensional plane and subjected to a magnetic field. As such, the circuit’s energies resemble those of a quantum oscillator with discrete energy levels. For a given magnetic flux, the lowest-energy states can be used to encode the GKP code words.
A qualitative analysis of the circuit predicts a robustness against common noise sources, such as charge and flux noise, making it a promising passive-QEC candidate. Clearly, the characteristics of the circuit needed to implement the new scheme require improvements of existing technology. For example, the fluxonium circuit should have a very large inductance, which isn’t currently attainable but will hopefully be possible in next generation designs. The proposed implementation of the hardware-encoded grid states represents a novel utilization of synthetic magnetism and a new application for gyrators based on the anomalous quantum Hall effect [7, 8]. It remains to be seen, however, whether these gyrators can successfully be married with two fluxonium circuits on-chip. Another question is whether an actively driven nonreciprocal on-chip device [5] could be a better alternative than a gyrator based on the anomalous quantum Hall effect.
This hardware-encoded GKP code implementation complements other ongoing efforts in designing intrinsically error-protected, superconducting circuit qubits, such as the realization of the qubit [9] and the proposal of the doubly nonlinear qubit, or dualmon [10]. All designs come with challenging demands on the parameters of the employed materials and of the circuit elements. Encouragingly, the implementation proposed by Rymarz and colleagues comes within feasible reach of near-future technology. Realizing GKP code words using superconducting circuits is especially promising, as it makes it relatively straightforward to implement a subset of logic gates called Clifford gates, which are required for fault-tolerant computation [2, 3]. The realization of an intrinsically robust computation unit is only the first step on the complex path towards fault-tolerant quantum computation. But every new design pushes the field of superconducting circuits towards new horizons.
References
- M. Rymarz et al., “Hardware-encoding grid states in a nonreciprocal superconducting circuit,” Phys. Rev. X 11, 011032 (2021).
- D. Gottesman et al., “Encoding a qubit in an oscillator,” Phys. Rev. A 64, 012310 (2001).
- P. Campagne-Ibarcq et al., “Quantum error correction of a qubit encoded in grid states of an oscillator,” Nature 584, 368 (2020).
- J. Koch et al., “Time-reversal-symmetry breaking in circuit-QED-based photon lattices,” Phys. Rev. A 82, 043811 (2010).
- K. M. Sliwa et al., “Reconfigurable Josephson circulator/directional amplifier,” Phys. Rev. X 5, 041020 (2015).
- A. Metelmann and A. A. Clerk, “Nonreciprocal photon transmission and amplification via reservoir engineering,” Phys. Rev. X 5, 021025 (2015).
- G. Viola and D. P. DiVincenzo, “Hall effect gyrators and circulators,” Phys. Rev. X 4, 021019 (2014).
- A. C. Mahoney et al., “On-chip microwave quantum Hall circulator,” Phys. Rev. X 7, 011007 (2017).
- A. Gyenis et al., “Experimental realization of an intrinsically error-protected superconducting qubit,” arXiv:1910.07542.
- D. T. Le et al., “Doubly nonlinear superconducting qubit,” Phys. Rev. A 100, 062321 (2019).