The universal behavior of a disordered system

Gil Refael

Viewpoint

The universal behavior of a disordered system

Department of Physics, California Institute of Technology, MC 114-36, Pasadena, California 91125

January 5, 2009• Physics 2, 1

The presence of disorder in a quantum many-body system may appear to make an already difficult problem nearly impossible to solve. However, scientists show that the details of the disorder often do not matter, allowing them to describe realistic systems from magnets to superconductors.

Figure caption — **Figure 1:** Fermions on the random-hopping chain. Instead of moving freely throughout the chain, fermions are confined to pairs of sites (connected by the arcs), which are often nearest neighbors, but can also be very far apart. The pair formation is scale invariant: if we zoom out, and only draw sites that are separated by a distance matching our new reduced resolution, the localization pattern looks the same.

The Landau theory of phase transitions and the concept of symmetry breaking provide a unifying description of even such seemingly different many-body systems as a paramagnet cooled to the verge of ferromagnetic order or a metal approaching the superconducting transition. What happens, however, when these systems can lose energy to their environment? For example, in rare-earth compounds called “heavy-fermion” materials, the $f$ -shell magnetic moments interact with a sea of mobile electrons [1]. Similarly, near the metal-superconductor transition in ultrathin wires, the electrons pair up in a connected network of small, superconducting puddles that are surrounded by a bath of unpaired metallic electrons [2]. The surrounding metal gives rise to a parallel resistive channel and hence dissipation. Introducing dissipation into a many-body quantum mechanical problem presented a theoretical challenge that was only resolved in the last quarter of the 20th century [3–5].

Phase transitions in quantum systems with both dissipation and disorder are, not surprisingly, even more complicated. Whether we like it or not, all experimental systems, and especially the examples above, have some degree of disorder such as a structural imperfection or the presence of impurities. Therefore understanding the effects of disorder is not merely an abstract intellectual challenge, it is necessary for explaining what we actually measure in these systems. In particular, even a small amount of disorder can have a big effect in low-dimensional quantum systems, where ordering is more difficult and interaction effects are enhanced. A notable example is Philip Anderson’s discovery of localization in metals (see his Nobel address [6]).

In a paper appearing in Physical Review B, Thomas Vojta and Chetan Kotabage of the Missouri University of Science and Technology and José Hoyos, now at Duke University, provide yet another example of the profound impact that disorder has on a large class of low-dimensional quantum systems [7]. In their paper, they derive the theory for a quantum phase transition in a one-dimensional system that is akin to both the magnetic and superconducting examples noted above: a chain of magnetic moments, whose motion is dissipative, and whose local interaction parameters are random. Unlike previous work, Vojta, Kotabage, and Hoyos tackle both dissipation and randomness on equal footing. Despite the complexity of this problem, they find the low-energy behavior of such dissipative random chains through a series of intuitive and simple arguments. Furthermore, they demonstrate that the low-energy behavior is independent of the type and amount of disorder in the chain. That is, it is universal.

To understand this perhaps unintuitive result, we first discuss the concept of universality and explain how it arises in random systems using a simple example. The term universality entered our vocabulary with the development of renormalization group theory, which was based on the realization that an important but overlooked symmetry of nature is scale invariance [8]. This symmetry is not omnipresent. Rather, it describes systems at critical points on the boundary between two phases, for instance, between a ferromagnet and a paramagnet. As a paramagnet is cooled to the verge of ferromagnetism, finite, strongly magnetized droplets start to form, albeit with each droplet pointing in a different direction. At the critical point, these droplets appear in all sizes, and if we zoom out, the size distribution of the droplets looks the same. But, if zooming out leaves the system looking the same, this is equivalent to saying that microscopic details are unimportant in determining the magnet’s behavior. This insensitivity to microscopic details is called universality. (We should add that in a quantum system, zooming out is tantamount to only looking at fluctuations on large length scales, or, equivalently, at the low-energy behavior.)

Typically, the description of a nondisordered, many-body quantum system begins with translational invariance and momentum conservation. Such a system of particles can be described by a set of states with a well-defined momentum denoted by the wave number $k$ . A useful example of a simple many-body problem that we can solve in this way is the one-dimensional “tight-binding” model of noninteracting fermions, in which each fermion is tightly bound to a site on a chain, but can hop to a neighboring site with probability $t$ . The energy spectrum for this model has a simple form: $ε_{k} = - 2 t cos (k)$ .

What happens, however, when translational invariance is broken? For our purposes, we can still use the hopping-fermion model, but let the hopping strength $t$ depend on where the fermion is on the chain: $t \Rightarrow t_{i}$ . Instinctively, we would anticipate that the appearance of nonuniformity in this fermion-hopping system would mangle the neat cosine form of the energy spectrum and replace it with a random and noisy spectrum that crucially depends on the details of how the hopping varies from site to site. Quite surprisingly, however, the opposite seems to occur: the disorder introduced through the randomness in the hopping gives rise to an energy spectrum of the fermion states that, albeit different from the pure system’s cosine spectrum, is essentially independent of the details of the disorder. This is also the essence of universality in disordered quantum systems: the low-energy physical properties are independent of the disorder distribution.

The system that Vojta, Kotabage, and Hoyos analyze has much in common with the simple fermion-hopping problem, and it can be solved by the same method: real-space renormalization group. Shang-keng Ma, Chandan Dasgupta, and Chin-kun Hu of the University of California, San Diego proposed this method in 1979 to solve the problem of random interactions between spins on a chain [9]. We can demonstrate and use their basic arguments to understand the random-hopping problem described above.

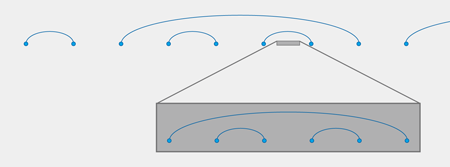
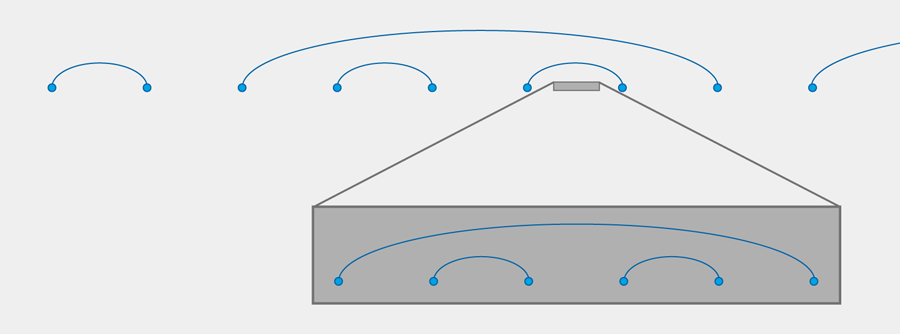
We begin by concentrating on the strongest hopping element, $t_{max}$ , and ignore everything else in the Hamiltonian as a much weaker perturbation. A fermion put in two neighboring sites, say 1 and 2, with $t_{max}$ hopping between them, can minimize its energy by choosing to be in the symmetric superposition $| ϕ 〉 = | 1 〉 + | 2 〉$ , which has the energy $ε_{-} = - t_{max}$ . In fact, this fermion gets stuck in this bond between the two sites, since anywhere else it would have a higher energy. But fermions from neighboring sites, say site 0, can also hop to site 1, locking the first fermion inserted in the bond between the two sites at site 2. This is an excited state with energy $ε = 0$ . This predicament can resolve itself with the fermion of site 2 hopping to site 3, leaving one fermion behind in the state $| ϕ 〉 = | 1 〉 + | 2 〉$ with energy of $ε = - t_{max}$ . This looks as if a fermion hopped directly from site 0 to site 3, leaving the two sites 1 and 2 untouched. So, we might as well forget sites 1 and 2 and solve a new Hamiltonian in which a small “renormalized” $t_{0, 3}$ connects sites 0 and 3. Repeating this procedure with the strongest bond at each stage will result in all fermions inserted localized between two sites, which can be arbitrarily far apart (Fig. 1). From this procedure, we can extract the energy of the fermions’ states: a fermion localized between two sites $L$ links apart will have a binding energy $E$ obeying ln $E \sim - (L)^{1 / 2}$ [10].

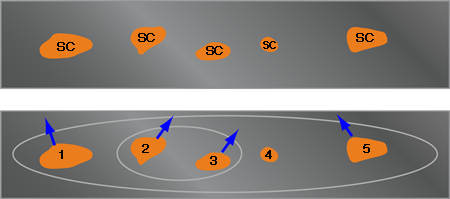
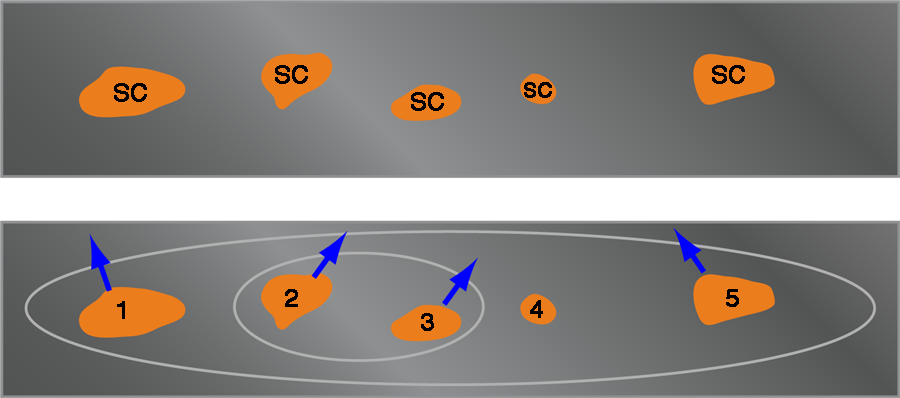
Vojta, Kotabage, and Hoyos have shown that a similar real-space analysis applies quite generally to dissipative disordered chains on the verge of a symmetry-breaking phase transition. Their focus is on a system that is similar to a chain of dynamically fluctuating magnetons (magnetic moments that can be described by a single variable). Each magneton interacts ferromagnetically with its nearest neighbors and has an energy scale $r_{i}$ associated with its dynamic fluctuations. These fluctuations compete with the energy scale $J_{i}$ that prefers neighboring magnetons to align with one another and seeks to establish magnetic order. Just as we solved the hopping-fermion problem above, Vojta, Kotabage, and Hoyos show that we can solve the disordered dissipative quantum magnet by either (a) iteratively eliminating the most fluctuating magneton (the moment with the largest $r_{i}$ ), which results in a ferromagnetic interaction between its neighbors, or (b) allowing the two most strongly interacting neighbors (i.e., those with the strongest $J_{i}$ between them), to unite and form a single magneton, with a renormalized lower energy scale, $r$ , of the dynamic fluctuations. A sketch of the resulting state is shown in the bottom of Fig. 2. This, they show, results in essentially the same universal behavior as is found in fermions in the random-hopping chain. Physically, this problem describes the critical behavior of superconducting puddles that form in a metallic wire right above the superconducting transition temperature (top of Fig. 2 ).

Vojta, Kotabage, and Hoyos go beyond solving the model to show that dissipative one-dimensional systems close to criticality are always susceptible to disorder. The ground-state properties of such systems cannot be analyzed using perturbation theory near the point of translational invariance. The results force us to reevaluate much of the research done on superconducting wires and magnetic chains, and to pose the question: How many other low-dimensional electronic systems can be described in the same way and have the same low-energy properties? What properties, so far taken for granted, are altered due to the presence of even a small amount of disorder? As the work of Vojta, Kotabage, and Hoyos proves, the combination of disorder, interactions, and low dimensionality (which enhances fluctuations) is bound to provide us with more surprises and fascinating examples of disorder-dominated phases, waiting to be discovered.

References

P. Coleman, in Handbook of Magnetism and Advanced Magnetic Materials, edited by H. Kronmüller and S. Parkin (Wiley-Interscience, New York, 2007)[Amazon][WorldCat]
A. Bezryadin, C. N. Lau, and M. Tinkham, Nature 404, 971 (2000)
A. O. Caldeira and A. J. Leggett, Ann. Phys. 149, 374 (1983)
J. A. Hertz, Phys. Rev. B 14, 1165 (1976)
A. J. Millis, Phys. Rev. B 48, 7183 (1993)
See http://nobelprize.org/nobel_prizes/physics/laureates/1977/anderson-lecture.pdf
T. Vojta, C. Kotabage, and J. A. Hoyos, Phys. Rev. B 79, 024401 (2009)
K. G. Wilson, Rev. Mod. Phys. 55, 583 (1983)
S. K. Ma, C. Dasgupta, and C. K. Hu, Phys. Rev. Lett. 43, 1434 (1979)
D. S. Fisher, Phys. Rev. B 50, 3799 (1994)

About the Author

Gil Refael earned a B.S. in math and physics from Tel-Aviv University in 1997. He did his graduate studies at Harvard University (under the supervision of Profs. Daniel S. Fisher and Eugene Demler), and obtained a Ph.D. in theoretical condensed matter physics in 2003. After being a postdoctoral fellow at the KITP, UC Santa Barbara, for two years, he joined the physics faculty at the Cailfornia Institute of Technology. His research interests involve a variety of problems of correlated quantum matter, both disordered and out of equilibrium. Gil is also grateful for current support as a Cottrell Scholar and a Packard Fellow.