Looking for parity violation in heavy-ion collisions

Berndt Müller

Viewpoint

Looking for parity violation in heavy-ion collisions

Department of Physics and Center for Theoretical and Mathematical Sciences, Duke University, Durham, NC 27708, USA

December 14, 2009• Physics 2, 104

The STAR detector at RHIC has measured a signal that may indicate parity violation occurs in metastable regions of the superdense matter.

Figure caption — **Figure 1:** When two nuclei collide with a nonzero impact parameter, their velocity vectors define a reaction plane (grey). The magnetic field $B$ created by the moving nuclei points, on average, in the direction of the relative angular momentum $L$ of the nuclei, perpendicular to the reaction plane. The presence of the magnetic field leads to a local violation of P and CP symmetry for strongly interacting, electrically charged particles (quarks). Because of this chiral magnetic effect, particles carrying charges of the same sign will be preferentially emitted into the same hemisphere (arrows $1$ and $2$ ); those with charges of opposite sign will be emitted into different hemispheres (arrows $1$ and $2^{'}$ ). Fluctuations of the charge symmetry with respect to the collision plane, which have been observed by the STAR Collaboration, may therefore be a signature of local parity violation.

When two heavy nuclei collide at high energy, they create strongly interacting matter at energy densities far above that of normal nuclei. This has been the route for creating new phases of matter composed of quarks and gluons for almost a decade at the Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Laboratory in the US. The measurements performed on collisions between two gold ( $Au - Au$ ) or two copper ( $Cu - Cu$ ) nuclei or between two protons ( $p - p$ ), with center-of-mass energies up to $200 GeV$ per nucleon pair, have shown that superdense, strongly interacting matter has an extraordinarily low shear viscosity (compared to its entropy) and is extremely opaque with respect to unbound quarks and gluons. [1,2]

Now, writing in Physical Review Letters, the STAR collaboration, whose detector is based at RHIC, reports results that may constitute evidence for the violation of parity—a fundamental symmetry that says that the physics of a system and its mirror image should be the same—in local domains of hot, strongly interacting matter [3]. Although the theory of quantum chromodynamics (QCD), which governs the strong interactions, does permit parity violation, experiments have so far put stringent limits on its presence.

Collisions between heavy nuclei produce some of the strongest magnetic fields that can be generated under laboratory conditions [4]. The moving nuclei generate a coherent magnetic field that, being long-ranged, acts as an “external” field on the quarks and gluons that make up the nuclei. Interesting effects arise when the magnetic field breaks the natural symmetries of the strong interaction between quarks. Magnetic fields are “odd” under time reversal—a charge moving backward in time creates a field in the opposite direction to the forward moving charge—so the presence of a magnetic field breaks time reversal symmetry in a quantum system. This aspect has been widely employed in the study of quantum chaos and has found many applications in condensed matter physics, such as in the quantum Hall effect.

Experimentally, the strong interactions respect space and time reflection symmetry to a very high degree: this has been established by precise experiments that set limits on the intrinsic electric dipole moment (EDM) of the neutron [5]. Yet the equations of QCD permit terms that violate time reversal symmetry. The present limit on the neutron EDM shows that a possible charge-parity (CP) violating term in the QCD Lagrangian is suppressed by at least a factor of $10$ trillion compared with its expected size. The reason for this suppression, or potentially the complete absence of the EDM, is not known, though one possibility is the existence of a new symmetry, called Peccei-Quinn symmetry [6], which must be broken in the vacuum and whose breaking would give rise to a light neutral, yet undiscovered particle, the axion [7].

There has been speculation for some time that the place to look for the violation of space and time reflection symmetry is in the new phases of nuclear matter that can be created in heavy-ion collisions [8,9]. In recent years, these speculations have focused [10,11] on possible domains of topologically twisted gluon fields that carry a nonvanishing expectation value (the topological charge) of what is called the pseudoscalar density. The pseudoscalar density is a scalar product of the chromoelectric and chromomagnetic field and changes sign under both parity (P) and charge-parity (CP) transformations. The existence of phases of quark-gluon matter with such properties is not forbidden by the laws of QCD, but it is unknown whether any such phase can be metastable and if so, whether it can be formed under the conditions prevailing in a nuclear collision. Even if such domains would be created, the sign of the expectation value of the pseudoscalar density would fluctuate from event to event, or several domains with different signs of the density would be formed in the same event. This makes the unambiguous detection of such a phenomenon difficult [12,13].

A recent theoretical breakthrough was the recognition [14,15] that the CP violating property of the strong magnetic fields naturally present in a heavy-ion collision could be used to probe the response of strongly interacting matter where the pseudoscalar density is expected to be odd with respect to CP. The leading manifestation of the interplay between electromagnetic and color fields with respect to CP symmetry is an effective interaction between fields coupling the topological charge density to the pseudoscalar invariant $E \cdot B$ [16]. In the normal QCD vacuum, where only baryons and mesons exist as free particles, the effective interaction is the well-known anomaly coupling $E \cdot B$ to the neutral pseudoscalar mesons $π^{0}$ , $η$ , $η'$ [17–20]. The interaction mediates, for example, the two-photon decays of the neutral pseudoscalar mesons.

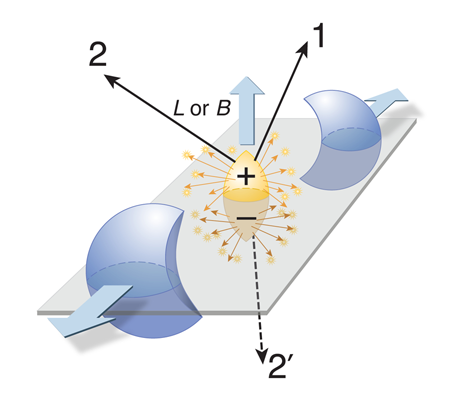
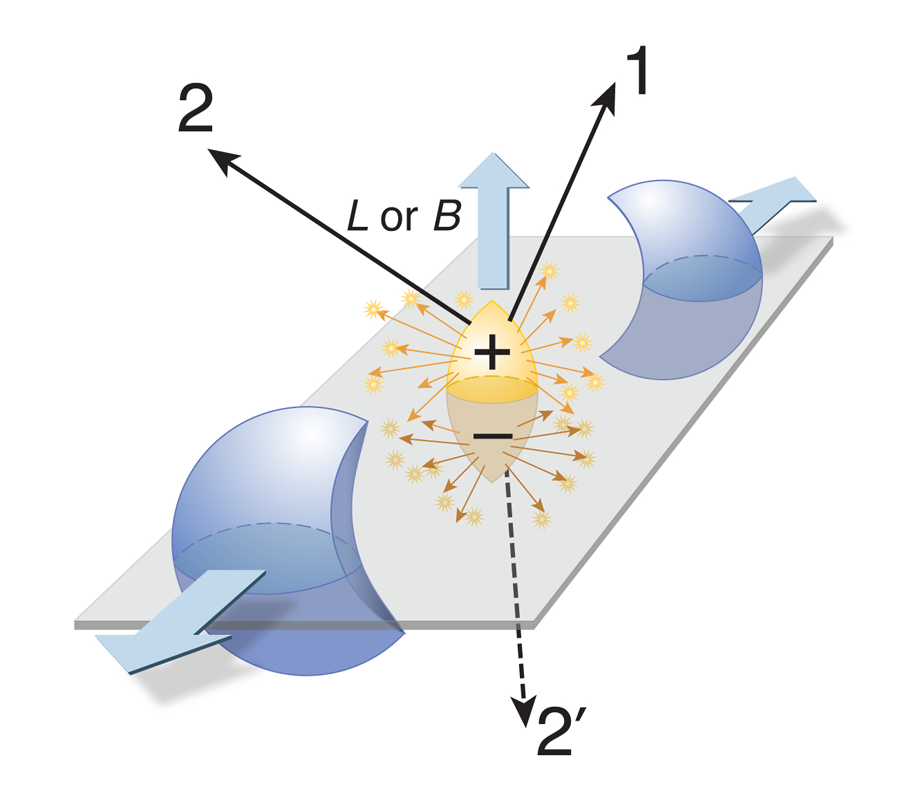
In the presence of an external magnetic field, this interaction can be shown to induce an anomalous, apparently P and CP violating, electromagnetic current pointing in the direction of the magnetic field. This has been called the chiral magnetic effect [15,21]. In an off-central heavy-ion collision, the magnetic field is preferentially oriented perpendicular to the reaction plane (see Fig. 1), pointing in the direction of the angular momentum of the two colliding nuclei. If the topological charge of the dense matter produced in the collision had a definite sign, this current would result in a separation of electrical charges with respect to the reaction plane. If, however, the sign of the pseudoscalar density fluctuates from point to point and event to event, as expected, only fluctuations of the electric charge asymmetry with respect to the reaction plane will be observed.

In the vacuum, nonperturbative configurations of the color field, called instantons, cause fluctuations of the pseudoscalar density; in the presence of thermal matter, fluctuations of the density grow in proportion to the energy density of the matter [22]. Within domains of a given sign of the density, the electric current induced by the chiral magnetic effect also has a uniform sign, resulting in charge separation in the direction of the magnetic field. This consequence of the CP violation is made visible by the violent explosion of the dense matter created in the collision: it will cause a slight charge asymmetry resulting in more “positive” particles exploding into one hemisphere and more “negative” particles into the other.

The STAR collaboration now reports positive results from measuring this asymmetry in $Au + Au$ collisions [3]. In order to detect the charge fluctuations, the STAR scientists used the two-particle correlation defined by $C_{12} = 〈 cos (ϕ_{1} + ϕ_{2} - 2 Ψ_{RP}) 〉$ , where $Ψ_{RP}$ denotes the azimuthal angle of the reaction plane [23]. $Ψ_{RP}$ can be easily determined in off-central collisions from the azimuthal anisotropy (the “elliptic flow”) of the emitted particles. By measuring $C_{12}$ for pairs of charged particles, the STAR scientists finds a clear positive correlation among like-sign charges emitted into the same hemisphere and a smaller positive correlation among unlike-sign charges emitted into opposite hemispheres (see Fig. 1). The strength of the correlation is found to increase with the impact parameter $b$ —a measure of the overlap between the colliding ions—as expected, since the net magnetic field grows with $b$ . The magnitude of the observed effect, $C_{12} \leq 5 \times 10^{- 4}$ , is consistent with the idea that thermal fluctuations of the topological charge density in a quark-gluon plasma, where quarks are liberated from their confinement into hadrons, are creating the domains in which P and CP symmetry is locally violated [14].

The question now is whether the STAR collaboration has reached the correct interpretation of their experimental observation, that is, whether their results are consistent with a sign of P or CP violation. Quantum mechanics does not forbid symmetry-violating quantities from fluctuating locally, so the STAR collaboration’s observation does not constitute direct evidence for local parity violation. Furthermore, the P and CP symmetry of the strong interactions are broken explicitly in the experiment by the presence of the magnetic field. It is also unclear whether the observed effect must be attributed to a new, deconfined phase of QCD matter, or whether interactions in the hadronic phase contribute to the observed effect. On the side of the experiment, the interesting questions that remain to be explored are how the observed effect depends on the collision energy and whether it is robustly and solely associated with the reaction plane.

References

I. Arsene et al., Nucl. Phys. A 757, 1 (2005); K. Adcox et al., 757, 184 (2005); B. B. Back et al., Nucl. Phys. A 757, 28 (2005); J. Adams et al., Nucl. Phys. A 757, 102 (2005)
B. Müller and J. L. Nagle, Ann. Rev. Nucl. Part. Sci. 56, 93 (2006)
B. I. Abelev et al., Phys. Rev. Lett. 103, 251601 (2009); arXiv:0909.1739 (nucl-ex); See also arXiv:0909.1717
J. Rafelski and B. Müller, Phys. Rev. Lett. 36, 517 (1976)
C. A. Baker et al., Phys. Rev. Lett. 97, 131801 (2006)
R. D. Peccei and H. R. Quinn, Phys. Rev. Lett. 38, 1440 (1977)
F. Wilczek, Phys. Rev. Lett. 40, 279 (1978)
T. D. Lee and G. C. Wick, Phys. Rev. 148, 1385 (1966)
P. D. Morley and I. A. Schmidt, Z. Phys. C 26, 627 (1985)
D. Kharzeev, R. D. Pisarski, and M. H. G. Tytgat, Phys. Rev. Lett. 81, 512 (1998)
D. Kharzeev and R. D. Pisarski, Phys. Rev. D 61, 111901 (2000)
S. A. Voloshin, Phys. Rev. C 62, 044901 (2000)
L. E. Finch, A. Chikanian, R. S. Longacre, J. Sandweiss, and J. H.Thomas, Phys. Rev. C 65, 014908 (2002)
D. E. Kharzeev, L. D. McLerran, and H. J. Warringa, Nucl. Phys. A 803, 227 (2008)
K. Fukushima, D. E. Kharzeev, and H. J. Warringa, Phys. Rev. D 78, 074033 (2008)
H. T. Elze, B. Müller, and J. Rafelski, in Proceedings of the International Workshop on Collective Excitations in Fermi and Bose Systems, Serra Negra, São Paulo, Brazil, 1998, edited by Carlos A. Bertulani, L. Felipe Canto, and M. S. Hussein (World Scientific, Singapore, 1999)[Amazon][WorldCat]; arXiv:hep-ph/9811372
J. S. Schwinger, Phys. Rev. 82, 664 (1951)
S. L. Adler, Phys. Rev. 177, 2426 (1969)
J. S. Bell and R. Jackiw, Nuovo Cimento A 60, 47 (1969)
B. L. Ioffe, Int. J. Mod. Phys. A 21, 6249 (2006)
D. E. Kharzeev and H. J. Warringa, Phys. Rev. D 80, 034028 (2009)
G. D. Moore, Phys. Lett. B 412, 359 (1997)
S. A. Voloshin, Phys. Rev. C 70, 057901 (2004)

About the Author

Berndt Müller received his Ph.D. in 1973 from the Goethe University in Frankfurt, Germany, for research on electrons in strong electric fields. After postdoctoral appointments at Yale University and the University of Washington, he joined the Goethe University faculty in 1976. Since 1990 he has been a member of the Physics Department at Duke University, where he holds the position of James B. Duke professor. From 1999 to 2004 he served as Dean of the Natural Sciences; since 2008 has headed the Duke Center for Theoretical and Mathematical Sciences. He received the Jesse Beams award of the Southeastern section of the American Physical Society in 2007. In recent years, the main focus of his research activities has been on relativistic heavy-ion collisions and the physics of the quark-gluon plasma.