Searching for the Higgs

Gail G. Hanson

Trend

Searching for the Higgs

Department of Physics and Astronomy, University of California, Riverside, Riverside, CA 92521, USA

December 14, 2009• Physics 2, 106

Researchers at the Large Hadron Collider are at the start of a challenging hunt for the Higgs boson, a particle thought to confer the property of mass on every other particle.

Since the 1970s, physicists have known that two fundamental forces of nature, the electromagnetic force and the weak force, can be unified into a single force—the electroweak force—if the particles that carry these forces are massless. The photon, which carries the electromagnetic force, is massless, but the particles that carry the weak force have substantial mass, explaining why the weak force is weaker than the electromagnetic force. This unification can still work if a new spin-zero boson, the Higgs boson, is introduced, allowing the particles that carry the weak force to be massive. In addition, interactions with the Higgs boson are responsible for the masses of all particles. These ideas form the basis of the standard model of particle physics, which is consistent with almost all observations. Gravity can act once particles have mass due to the Higgs boson—the Higgs boson is not the source of the gravitational force. The one outstanding missing piece in this entire picture is the Higgs boson itself. What are the prospects for its discovery?

The standard model of particle physics and the Higgs boson

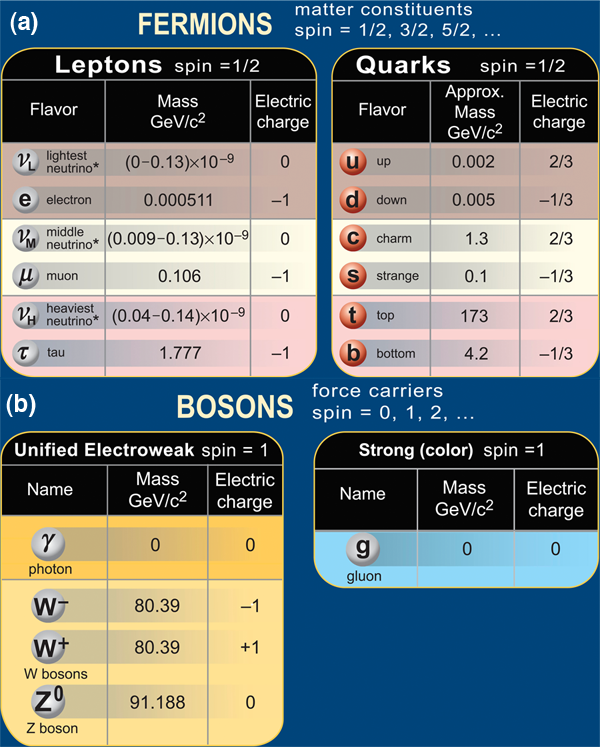
Matter is made up of spin- $1 / 2$ fermions, the particles known as leptons (the “light ones”) and quarks. There are three families of leptons, each consisting of two particles: the electron with its corresponding neutrino ( $ν$ ), the muon ( $μ$ ) and its neutrino, and the tau lepton ( $τ$ ) and its neutrino [1]. Electrons are familiar from electric current and as constituents of atoms; they are the lightest electrically charged particles. Muons and tau leptons are also charged and can be considered to be heavier electrons. Neutrinos are neutral and (almost) massless. All of the leptons can be directly observed, some more easily than others.

Quarks also come in three families, and they also have electrical charge, but their charges are fractions of the charge of the electron ( $+ 2 / 3$ and $- 1 / 3$ ). They cannot be directly observed—the particles we do observe, such as the proton and the pion, are made up of either three quarks or a quark and its antiparticle, an antiquark. Every particle has a corresponding antiparticle with the same mass but opposite charge, for example, the antiparticle of the electron is the positively charged positron. Quarks that are produced in particle interactions or decays materialize as “jets” of ordinary particles collimated close to the original quark direction [2].

Four fundamental forces act on the fundamental fermions: gravity, the weak force (responsible for nuclear beta decay), the electromagnetic force, and the strong force. These forces occur through the exchange of fundamental bosons: the graviton, the charged and neutral $W$ and $Z$ bosons, the photon, and eight gluons. (Gravity will not be discussed further here.) All of the fundamental fermions have interactions via the weak force, and all of the charged fundamental fermions have electromagnetic interactions. Only the quarks can interact via the strong force, and particles such as protons that are made up of quarks and therefore have strong interactions are called hadrons (the “heavy ones”). The fundamental particles and forces are summarized in Fig. 1.

Figure caption — **Figure 1:** The fundamental fermions and force carrying bosons of the standard model. (a) All matter is made up of leptons and quarks, which are spin- $1 / 2$ fermions. There are three families of leptons and three families of quarks. (b) The interactions between the fundamental particles occur through the exchange of bosons: the photon for the electromagnetic force, $W^{+}$ , $W^{-}$ , and $Z^{0}$ for the weak force, and gluons for the strong force. (From Ref. [3].)

Photons, which have no mass, carry the electromagnetic force, whereas the massive charged $W$ and neutral $Z$ are responsible for the weak interactions; all of these particles are spin-one bosons. The minimal standard model [4] requires in addition a massive scalar boson, the Higgs boson, to allow the $W$ and $Z$ to be massive, as described by the Higgs mechanism [5]. The lowest energy state of the Higgs field has a nonzero value, which has the dimensions of mass. Particles obtain their mass from their interactions with this Higgs field—this is the reason the Higgs boson plays such a major role in physics. The photon has no such interactions, so it retains its massless character, while the masses of the $W$ and $Z$ are approximately $100$ times the mass of the proton. The asymmetry between the masses of the photon and the $W$ and $Z$ bosons is called “electroweak symmetry breaking.”

According to theory, the Higgs occurs as a doublet of complex scalar fields, giving four degrees of freedom. Three of the four degrees of freedom are unphysical but are needed as intermediate states in the theory, while the fourth degree of freedom corresponds to the single physical Higgs boson. Once the Higgs mechanism is included, the electromagnetic and weak interactions are unified into one interaction—the electroweak interaction [6].

The Higgs boson, or something else that plays its role, is necessary in the standard model, but it has not yet been observed. Therefore its discovery is of utmost importance in particle physics. Searches have most recently been carried out at the Large Electron Positron collider (LEP) at the European Organization for Nuclear Research (CERN) [7] and at the Tevatron proton-antiproton collider at Fermilab [8]. It is most likely, however, that it will be discovered at the Large Hadron Collider (LHC) [9] at CERN.

At what mass should we be looking for the Higgs? The mass of the Higgs boson is not specified in the standard model, but theorists think that it should be less than about $1000 GeV$ (about $1000$ times the mass of the proton). In certain extensions of the standard model such as supersymmetry there may be other constraints on the mass. The couplings of the Higgs boson to other particles determine its production rate and its decays to other particles, and knowing these coupling strengths within the theory allows the prediction of its decays as functions of its unknown mass alone.

Couplings of the Higgs boson to other elementary particles are directly related to its role in generating their masses. The Higgs boson is produced in interactions involving heavy particles, and its decays are in general into the heaviest particles that are kinematically possible. If the Higgs boson is heavier than twice the mass of the $W$ boson, it decays primarily into $W^{+} W^{-}$ and $Z Z$ . If it is lighter, its decays to pairs of heavy fermions (a $b$ quark and its antiparticle the $\bar{b}$ quark, or a tau lepton $τ^{-}$ and its antiparticle the $τ^{+}$ ) become dominant [10].

Indirect limits on the Higgs boson mass

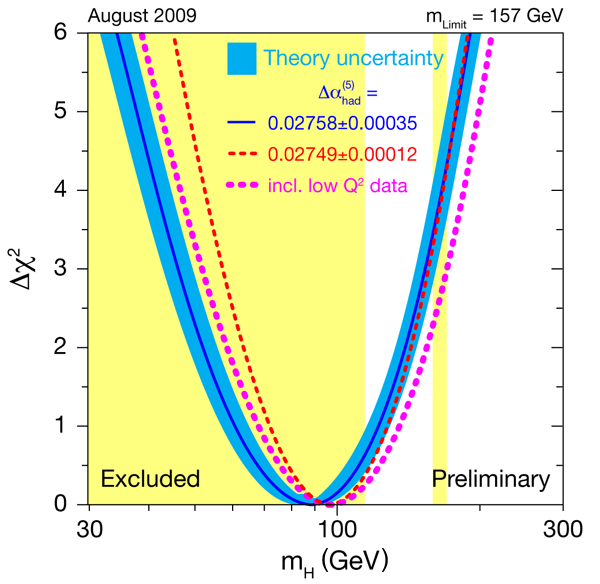
The value of the Higgs boson mass affects the standard model predictions for electroweak quantities, such as the mass and width of the $W$ boson and the width and other parameters of the $Z$ boson, measured in electron-positron colliders, hadron colliders, and elsewhere through higher-order corrections to the basic calculations, which are dependent logarithmically on the Higgs mass. (Such corrections are dependent on the square of the top quark mass and accurately predicted it before the top quark was discovered.) These electroweak quantities have been measured extremely precisely, for example at LEP, and global fits to the data with the standard model Higgs mass as a free parameter provide limits on the Higgs boson mass, as shown in Fig. 2 [11]. The quantity $χ^{2}$ is a statistical measure of the agreement of the fit with the data, with the minimum value, $χ_{min}^{2}$ , at the most probable value of the Higgs mass. The global electroweak fit yields $Δ χ^{2} = χ^{2} - χ_{min}^{2} = 1$ limits, corresponding to a $68 %$ confidence level or one standard deviation errors on the Higgs mass of

m_{H} = 87_{- 26}^{+ 35} GeV

(1)

or a one-sided $95 %$ confidence-level upper limit, including the band of theoretical uncertainty, on $m_{H}$ of $157 GeV$ . Precision electroweak fits thus prefer a relatively low-mass Higgs boson.

The Higgs boson in supersymmetric models

Supersymmetric extensions of the standard model [12,13] are particularly interesting on theoretical grounds. In supersymmetric theories there is a link between fermions and bosons. Every particle has a supersymmetric partner with the same properties except that fermions have supersymmetric partners that are bosons, and bosons have supersymmetric partners that are fermions. For example, the supersymmetric partner of the electron, a spin- $1 / 2$ fermion, is the spin- $0$ scalar electron, or selectron; the supersymmetric partner of the spin- $1 / 2$ top quark is the spin- $0$ stop quark; and the supersymmetric partner of the spin- $1$ gluon is the spin- $1 / 2$ gluino. Since such supersymmetric partners of the known particles have not been discovered, supersymmetry is broken, that is, the partners have larger masses than the known particles. Supersymmetric theories provide a consistent framework for the unification of the interactions at a high-energy scale and for the stability of the electroweak scale. Supersymmetry appears to be essential for string theory. In many supersymmetric models, the Lightest Supersymmetric Particle (LSP) is stable (it does not decay) and is a candidate for dark matter [14]. The measurement of the muon anomalous magnetic moment is significantly inconsistent with the standard model [15] and may be accounted for by supersymmetry.

A general property of any supersymmetric extension of the standard model is the presence of at least two Higgs doublets, but there can be more. The simplest supersymmetric model is the minimal supersymmetric extension of the standard model (MSSM) [13]. In the MSSM there are two Higgs doublets, resulting in five physical Higgs bosons: three neutral ( $h$ , $H$ , and $A$ ) and two charged ( $H^{\pm}$ ). Masses and couplings in the MSSM depend on standard model parameters plus at least two other parameters, tan $β$ and a mass parameter (usually $m_{A}$ ). The mass of the lightest Higgs boson, $m_{h}$ , is less than the mass of the $Z$ , $m_{Z}$ , at the basic level and thus it was thought that it could have been found at LEP. However, $m_{h}$ is increased significantly by corrections due primarily to the effects of the top quark and its supersymmetric partner, the spin- $0$ stop quark. Calculations within the MSSM and other supersymmetry models obtain an upper limit for $m_{h}$ of typically about $130 GeV$ [13]. Thus the lightest Higgs boson must be relatively light, as favored by the precision electroweak data. In fact, fits to the precision electroweak data within the constrained minimal supersymmetric standard model (CMSSM) give [16]

m_{h} = 110_{- 10}^{+ 8} (exp) \pm 3 (theor) GeV .

(2)

In the decoupling limit, $m_{A}^{2} ≫ m_{Z}^{2}$ , the lightest neutral Higgs boson $h$ couples in much the same way as the standard model Higgs. The $H$ , $A$ , and $H^{\pm}$ are much heavier and nearly degenerate.

Searches at electron-positron colliders

Direct searches for the standard model Higgs boson were carried out at the LEP electron-positron collider, running at center-of-mass energies of $91$ to $209 GeV$ , up until the end of 2000, the final year of the LEP program. The four LEP experiments were ALEPH [17], DELPHI [18], L3 [19], and OPAL [20]. In electron-positron colliders the Higgs boson would be produced in association with a $Z$ : $e^{+} e^{-} \to H Z$ (that is, a high-energy collision between an electron and a positron would create a Higgs plus a $Z$ boson). Since electrons and positrons are fundamental particles, the collision makes use of their full energy.

The Higgs and $Z$ bosons were searched for by reconstructing them from their decay products. At LEP energies, the kinematic limit for the mass of the Higgs boson is about $115 GeV$ , so the dominant decay of the Higgs would be into a pair of $b$ quarks, with smaller fractions of tau lepton pairs, $W$ pairs (one $W$ is virtual, that is, its mass is not equal to the rest mass of the $W$ boson), or gluon pairs. An important constraint was the reconstruction of the mass of the accompanying $Z$ through its decay products, and identification of $b$ quarks was also used. The event configurations searched were the four-jet final state ( $H \to b \bar{b}$ , $Z \to q \bar{q}$ ), the missing energy final state ( $H \to b \bar{b}$ , $Z \to v \bar{v}$ ), the leptonic final state ( $H \to b \bar{b}$ , $Z \to e^{+} e^{-}$ or $H \to b \bar{b}$ , $Z \to μ^{+} μ^{-}$ ), and the tau lepton final state ( $H \to b \bar{b}$ , $Z \to τ^{+} τ^{-}$ or $H \to τ^{+} τ^{-}$ , $Z \to q \bar{q}$ ).

Reconstructing these decays requires an array of methods that have been designed into the experiments and used for other physics as well. Charged particles leave trails in tracking devices, such as drift chambers or silicon detectors, and their momenta can be measured from how much they bend in a magnetic field. Neutral particles such as photons leave energy deposits in the detectors. Electrons and muons are identified through their interactions with the material of the detector. Neutrinos do not interact with the amount of material in the detector and so are identified by missing energy in the reconstruction of the event, since the total energy is known from the center-of-mass energy of the electron-positron collision. Quarks are reconstructed from the jets of particles they produce, charged or neutral, since quarks cannot be directly observed. Jets from $b$ quarks can be distinguished by the rather long lifetimes of the hadrons containing the $b$ quarks. These hadrons decay at some distance from the overall event production point along the beams, and this displacement can be measured in precision tracking devices.

When searching for the Higgs boson, physicists look for events that meet the criteria expected for the Higgs. However, there are background events, which are those from other physics processes that mimic the characteristics of the Higgs signal. There are significant numbers of background events due to $W$ pairs and $Z$ pairs, which appear as four-fermion events due to their decays, and quark-antiquark events. A signal due to Higgs boson production would appear as an excess number of events compared with these known standard model backgrounds.

No statistically significant evidence was found for the Higgs boson, and a combination of the data of the four experiments gave a lower limit of $m_{H} > 114.4 GeV$ at the $95 %$ confidence level [21]. However, in the last year of LEP running at center-of-mass energies above $206 GeV$ , some excess events were seen that were consistent with background plus a Higgs boson of mass about $115 GeV$ [22]. The experiments requested an extension of the LEP program for six months, but the request was denied because it would delay the construction of the LHC, which was built in the same tunnel as LEP.

The four LEP experiments also searched for neutral Higgs bosons as predicted by the MSSM. The numbers of events produced and Higgs decays in the MSSM are determined by the parameters of the particular MSSM model, so the interpretations of search results depend on these parameters. The lightest Higgs boson $h$ typically decays into a pair of $b$ quarks or a pair of tau leptons, and the main production mechanisms are $e^{+} e^{-} \to h Z$ and $e^{+} e^{-} \to h A$ , so searches for the standard model Higgs boson can be interpreted within the MSSM. The searches of the four LEP experiments were combined to give limits on $m_{h}$ and $m_{A}$ of about $93 GeV$ at $95 %$ confidence level over most of the MSSM parameter space [23]. The limit on $m_{h}$ gradually approaches that of the standard model Higgs in the decoupling limit. In summary, no statistically significant evidence for a Higgs boson was obtained at LEP.

Searches at hadron colliders

Plans were for Higgs boson searches to take place at the Superconducting Super Collider (SSC), a $40$ - $TeV$ (one $TeV$ equals $1000 GeV$ ) proton-proton collider that had started construction in Texas but was canceled in 1993. However, after LEP the search for the Higgs boson then moved to Fermilab as an upgraded collider and experiments began data taking. At proton-proton or proton-antiproton colliders, unlike at electron-positron colliders, the colliding particles are not fundamental. Protons (antiprotons) are made up of quarks (antiquarks) and gluons, so the collisions involve quarks with quarks (antiquarks) or gluons, or gluons with gluons. The energies of the quarks or gluons within the proton or antiproton vary as steeply falling functions of the fraction of the total energy of the proton or antiproton. Therefore the effective center-of-mass energy of the collision is in general much less than that of the colliding protons and antiprotons and varies over a wide range. The energy transverse to the beam direction roughly balances since the quarks and gluons travel in the same direction as the proton or antiproton.

To date, searches for the standard model Higgs boson have been performed at the Fermilab Tevatron proton-antiproton collider at a center-of-mass energy of $1.96 TeV$ in the CDF [24] and D0 [25] experiments. The dominant production mechanism for Higgs bosons at the Tevatron would be through the interaction of a gluon in a proton with a gluon in an antiproton (gluon-gluon fusion). The Higgs can also be produced in association with a $W$ or $Z$ boson through the interaction of a quark in a proton with an antiquark in an antiproton (similar to the production of $H Z$ in an electron-positron collider).

With the data accumulated so far, the Tevatron experiments are sensitive only to high-mass Higgs bosons that decay into $W$ pairs. Searches for low-mass Higgs bosons are more difficult and require more data—there are very large backgrounds that mask evidence for a low-mass Higgs decaying into a pair of $b$ quarks or a pair of tau leptons. In order to control these backgrounds, researchers look for the low-mass Higgs in association with a $W$ or $Z$ boson, which reduces the number of possible Higgs events. In addition, the low-mass Higgs boson must be identified by reconstructing it from a pair of $b$ -quark jets. There are still large numbers of background events, even with the requirement of identifying an accompanying $W$ or $Z$ , and the mass peak from the pair of $b$ quarks must be well defined in order to observe it above the background.

To search for a Higgs that decays into a pair of $W$ ’s, the subsequent decays of the $W$ into a lepton ( $e$ , $μ$ , or $τ$ ) and a neutrino are used. The signature for the Higgs is therefore events with two energetic electrons with opposite charge, or two muons with opposite charge, or an electron and a muon with opposite charge, plus large missing transverse energy due to the two neutrinos, which are not detected. (The tau contributes through its decay to an electron or a muon.) The main background is due to electromagnetic production of a pair of oppositely charged leptons when a quark-antiquark annihilation occurs (the Drell-Yan process), which is suppressed by the requirement of large missing transverse energy. Other backgrounds are due to $W W$ , $Z Z$ , $W Z$ , and top quark pair production with subsequent decays into leptons. Both experiments compare the numbers of events observed with the numbers of background events expected, plus a possible signal due to a standard model Higgs boson of assumed mass produced at the predicted rate in the standard model. They use statistical methods to determine upper limits (at the $95 %$ confidence level) on the possible production rate for the Higgs boson compared with the standard model prediction. Neither experiment by itself can set a $95 %$ confidence level upper limit below the standard model prediction (exclusion), but the combined results of the two experiments exclude a standard model Higgs boson of mass between $160$ and $170 GeV$ [26]. Discovery of a Higgs boson with mass in the region $115$ – $120 GeV$ by the Tevatron is unlikely [27].

The Large Hadron Collider (LHC) at CERN, which will begin data taking with proton-proton collisions in early 2010 and will ultimately have a center-of-mass energy of $14 TeV$ , will be sensitive to the entire mass range of the standard model Higgs boson. Searches for the Higgs boson will then begin in the ATLAS [28] and Compact Muon Solenoid (CMS) [29] detectors. The most important production mechanisms for the Higgs at the LHC are similar to those at the Tevatron. The Higgs decay into $W$ or $Z$ pairs will be used for the high-mass region. For a low-mass Higgs boson, decays into pairs of $b$ quarks or $τ$ leptons dominate; however, backgrounds from ordinary quarks and gluons are expected to be too large at the LHC to make these decay modes possible for a Higgs search. Therefore the search for the low-mass Higgs will rely on the decay into two photons, with a decay fraction of only about $0.002$ . There is still considerable background in the two-photon channel due to real photon pairs produced in standard model processes and jets misidentified as photons, so the Higgs will be seen as a small peak on top of a large background [30,31]. Accurate reconstruction of the photons in the detector is needed for the best definition of the peak.

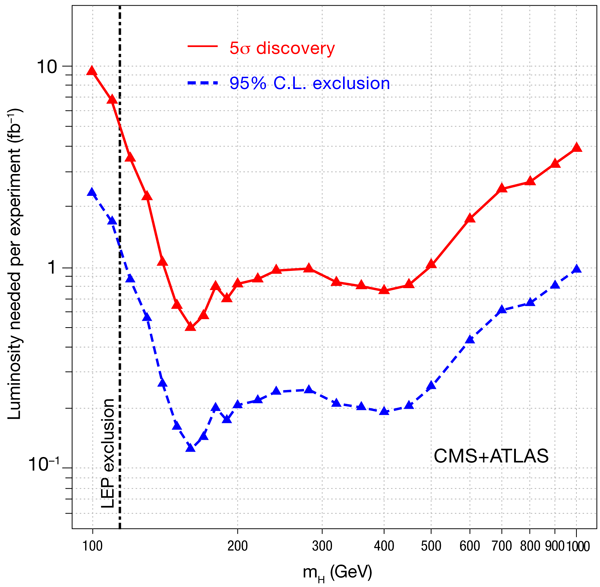
Finding a relatively light Higgs boson (which seems likely judging from the fits to precision electroweak data) at the LHC will be difficult and will require—in the language of high-energy physicists—several ${fb}^{- 1}$ of integrated luminosity [32], as shown in Fig. 3. In this context, luminosity is a measure of the collision rate of the two beams, and integrated luminosity of the number of collisions. One ${fb}^{- 1}$ of integrated luminosity corresponds to the production of one event for a process with a theoretical cross section of $1 fb$ and is thus a measure of the amount of data that needs to be acquired. In practical terms, it means two to three years of data taking after the LHC begins operation at full energy will be required for observation of the Higgs boson. It may be that a Higgs boson of mass $115 GeV$ , just above the LEP limit, will be found. If this Higgs is the lightest MSSM Higgs boson, then it is possible that supersymmetry will be discovered first since the supersymmetric partners of quarks and gluons, the squarks and gluinos, could be produced copiously. This will be truly exciting!

Acknowledgments

The author acknowledges support by the Department of Energy through grants DE-FG02-07ER41465 and DE-FG02-07ER41487 and by the National Science Foundation through grants PHY-0630052 and PHY-0612805. The author would also like to acknowledge fruitful discussions with students and colleagues, especially Nina Byers, Ernest Ma, Harry Tom, and Gillian Wilson.

References

C. Amsler et al. (Particle Data Group), Phys. Lett. B 667, 1 (2008); and 2009 partial update for the 2010 edition, http://pdg.bl.gov
G. Hanson et al., Phys. Rev. Lett. 35, 1609 (1975)
Contemporary Physics Education Project, http://cpepweb.org
S. Weinberg, Phys. Rev. Lett. 19, 1264 (1967); A. Salam, Elementary Particle Theory, edited by N. Svartholm (Almquist and Wiksells, Stockholm, 1968), p.367
P. W. Higgs, Phys. Lett. 12, 132 (1964); F. Englert and R. Brout, Phys. Rev. Lett. 13, 321 (1964); P. W. Higgs, 13, 508 (1964); Phys. Rev. 145, 1156 (1966)
For reviews, see J. F. Gunion, H. E. Haber, G. L. Kane, and S. Dawson, The Higgs Hunter Guide (Addison-Wesley, Reading, Massachusetts, 1990)[Amazon][WorldCat]; J. Ellis, G. Ridolfi, and F. Zwirner, C. R. Physique 8, 999 (2007); A. Djouadi, Phys. Rep. 457, 1 (2008)
CERN official web site http://public.web.cern.ch/public/; John Adams Memorial Lecture, CERN, November 26, 1990, http://sl-div.web.cern.ch/sl-div/history/lep_doc.html
Fermilab official web site http://www.fnal.gov; R. R. Wilson, “The Tevatron,” FERMILAB-TM-0763 (1978)
LHC official web site http://public.web.cern.ch/public/en/LHC/LHC-en.html
A. Djouadi, J. Kalinowski, and M. Spira, Comput. Phys. Commun. 108, 56 (1998)
The ALEPH, CDF, D0, DELPHI, L3, OPAL, SLD Collaborations, the LEP Electroweak Working Group, the Tevatron Electroweak Working Group, the SLD Electroweak, and Heavy Flavour Groups, arXiv:0811.4682v1 (hep-ex) (2008); updates for Summer 2009 from http://lepewwg.web.cern.ch/LEPEWWG/
J. Wess and B. Zumino, Nucl. Phys. B70, 39 (1974); Phys. Lett. B 49, 52 (1974); P. Fayet, 69, 489 (1977); 84, 421 (1979); 86, 272 (1979)
For reviews with references to the original literature, see H. E. Haber, and G. L. Kane, Phys. Rep. 117, 75 (1985); H. E. Haber, Phys. Rev. D 66, 010001 (2002); S. P. Martin, arXiv:hep-ph/9709356v5 (2008); A. Djouadi, Phys. Rep. 459, 1 (2008); Eur. Phys. J. C 59, 389 (2009)
J. R. Ellis, J. S. Hagelin, D. V. Nanopoulos, and M. Srednicki, Phys. Lett. B 127, 233 (1983); J. R. Ellis, J. S. Hagelin, D. V. Nanopoulos, K. A. Olive, and M. Srednicki, Nucl. Phys. B 238, 453 (1984); H. Goldberg, Phys. Rev. Lett. 50, 1419 (1983)
G. W. Bennett et al., Phys. Rev. D 73, 072003 (2006)
O. Buchmueller et al., Phys. Lett. B 657, 87 (2007)
ALEPH Collaboration, Nucl. Instrum. Methods A 294, 121 (1990); 360, 481 (1995); D. Creanza et al., 409, 157 (1998)
P. Aarnio et al. (DELPHI Collaboration), Nucl. Instrum. Methods A 303, 233 (1991); P. Abreu et al. (DELPHI Collaboration), 378, 57 (1996); P. Chochula et al. (DELPHI Silicon Tracker Group), 412, 304 (1998)
B. Adeva et al.(L3 Collaboration), Nucl. Instrum. Methods A 289, 35 (1990); O. Adriani et al. (L3 Collaboration), Phys. Rep. 236, 1 (1993); J. A. Bakken et al., Nucl. Instrum. Methods A 275, 81 (1989); O. Adriani et al., 302, 53 (1991); B. Adeva et al., 323, 109 (1992); K. Deiters et al., 323, 162 (1992); M. Chemarin et al., 349, 345 (1994); M. Acciarri et al., 351, 300 (1994); G. Basti et al., 374, 293 (1996); A. Adam et al., 383, 342 (1996)
K. Ahmet et al. (OPAL Collaboration), Nucl. Instrum. Methods A 305, 275 (1991); S. Anderson et al., 403, 326 (1998); B. E. Anderson et al., IEEE Trans. Nucl. Science 41, 845 (1994); G. Aguillion et al., Nucl. Instrum. Methods A 417, 266 (1998)
R. Barate et al. (ALEPH, DELPHI, L3, OPAL Collaborations, and The LEP Working Group for Higgs Boson Searches), Phys. Lett. B 565, 61 (2003)
R. Barate et al. (ALEPH Collaboration), Phys. Lett. B 495, 1 (2000); M. Acciarri et al. (L3 Collaboration), 495, 18 (2000); G. Abbiendi et al. (OPAL Collaboration), 499, 38 (2001); P. Abreu et al. (DELPHI Collaboration), 499, 23 (2001)
The ALEPH, DELPHI, L3, OPAL Collaborations, and The LEP Working Group for Higgs Boson Searches, Eur. Phys. J. C 47, 547 (2006)
D. Acosta et al. (CDF Collaboration), Phys. Rev. D 71, 032001 (2005); R. Blair et al., “The CDF II Detector Technical Design Report,” Report No. FERMILAB-PUB-96 390-E
D0 Collaboration, Nucl. Instrum. Methods A 565, 463 (2006)
The Tevatron New Phenomena and Higgs Working Group for the CDF and D0 Collaborations, FERMILAB-PUB-09-060-E, arXiv:0903.4001v1 (hep-ex) (2009)
J. Conway, “The Search for the Higgs Boson,” plenary presentation at the 2009 Europhysics Conference on High Energy Physics, Kraków, Poland, July 2009, http://indico.ifj.edu.pl/MaKaC/contributionDisplay.py?contribId=937&sessionId=31&confId=11
G. Aad et al., JINST 3, S08003 (2008)
R. Adolphi et al., JINST 3, S08004 (2008)
ATLAS Physics Performance Technical Design Report, CERN/LHCC/99-15; S. Asai et al., Eur. Phys. J. C 32, Suppl. 2, 19 (2004); arXiv:hep-ph/0402254
CMS Physics, Technical Design Report, vol. II: Physics Performance, CERN/LHCC 2006-021, CMS TDR 8.2
J.-J. Blaising et al. “Potential LHC Contributions to Europe’s Future Strategy at the High-Energy Frontier,” (2006), http://council-strategygroup.web.cern.ch/council-strategygroup/BB2/contributions/Blaising2.pdf.; F. Gianotti, “ATLAS: preparing for the first LHC data,” plenary presentation at the 2009 Europhysics Conference on High Energy Physics, Kraków, Poland, July 2009, http://indico.ifj.edu.pl/MaKaC/contributionDisplay.py?contribId=940&sessionId=32&confId=11

About the Author

Gail G. Hanson received her B.S. degree in physics in 1968 from the Massachusetts Institute of Technology. She began work in experimental particle physics as an undergraduate. She received her Ph.D. degree in 1973 also from the Massachusetts Institute of Technology for research on the electron-positron collider at the Cambridge Electron Accelerator at Harvard University. She did postdoctoral research at the Stanford Linear Accelerator Center (SLAC), working on the SPEAR electron-positron storage ring, where she contributed to the discoveries of the J/ $ψ$ particle and the $τ$ lepton and independently discovered quark jets in 1975, for which she was awarded the American Physical Society’s W. K. H. Panofsky Prize. Hanson continued in staff physicist positions at SLAC until 1989, when she moved to Indiana University to become a Professor of Physics. In 1997, she became a Distinguished Professor at Indiana University. She continued research on electron-positron physics on the PEP storage ring and the SLAC Linear Collider at SLAC and on the OPAL experiment at the LEP electron-positron collider at CERN, where she served as Physics Coordinator and contributed to $b$ -quark hadron discoveries and searches for new particles. In 2002, she moved to the University of California, Riverside, as a Distinguished Professor of Physics. Hanson now carries out research on the Compact Muon Solenoid (CMS) experiment at the Large Hadron Collider (LHC) at CERN and on development of a future $μ^{+} μ^{-}$ collider. Hanson was elected a Fellow of both the American Physical Society and the American Association for the Advancement of Science.