Playing with the geometry of oxide heterostructures

Elbio Dagotto

Viewpoint

Playing with the geometry of oxide heterostructures

Department of Physics and Astronomy, The University of Tennessee, Knoxville, TN 37996
and Materials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, TN 32831

February 9, 2009• Physics 2, 12

Researchers bring the prospect of new electronic devices based on oxide materials closer to reality by doping interfaces via polar discontinuities rather than chemical substitution.

Figure caption — **Figure 1:** Schematic diagram of possible reconstruction processes. (a) Stacking of $- 1$ and $+ 1$ layers, where $E$ is the electric field and $- V$ the electrostatic potential. In this case, the potential diverges since there is no reconstruction. (b) A structure in which the top layer of the V oxide portion of the system reconstructs to a charge $- 1 / 2$ . The electrostatic potential does not diverge in this case. (c) Another example where there is no divergence. In this case, the surface is reconstructed to a charge $- 1 / 2$ . The competition between (b) and (c) is the key observation reported by Higuchi *et al.* [2].

Strongly correlated electron (SCE) compounds exhibit a wide range of exotic and intellectually challenging phenomena [1], such as high-temperature superconductivity in copper oxides, colossal magnetoresistance (CMR) in manganese oxides, and the more recently unveiled, totally unexpected, superconductivity in layered iron pnictides. In these materials, novel phases are often stabilized by altering the density of conduction electrons via chemical substitution. While chemical doping is widely successful, it remains unsatisfactory because it is invariably accompanied by disorder. Sometimes disorder plays a key role, such as amplifying the range of couplings where the CMR effect occurs, but in other cases disorder masks the true clean-limit phase diagrams of some compounds and it may reduce their critical temperatures [1]. Now, in a paper appearing in Physical Review B, T. Higuchi, Y. Hotta, T. Susaki, A. Fujimori, and H. Y Hwang from the University of Tokyo, Japan, have demonstrated disorder-free hole doping in oxide heterostructures by exploiting polar discontinuities [2].

It has recently become possible to make heterostructures of complex oxides, by stacking nanometer scale thin films with atomically smooth interfaces [3]. This breakthrough is important for a variety of reasons. For instance, it allows us to imagine a new class of microelectronic devices made from oxide materials [4]. Namely, if oxides can be prepared in heterostructures similar to those employed in standard electronic devices based on semiconductors, then the richer properties of SCE, as compared to band insulators, may lead to novel functionalities.

Further, atomically precise oxide heterostructures can also advance basic science by stabilizing exotic new phases at the interfaces. This can occur because typically the two materials defining an interface tend to have different conduction electron concentrations and chemical potentials, thus leading to a transfer of charge from one to the other. This charge transfer, stabilizing a different density from the materials on either side, occurs only near the interface, since long-range Coulomb interactions between the electronic carriers and the positively charged ions would prevent the spreading of the transferred charge. Also, the strain at the interface, caused by the different atomic spacing of the components, may lead to interfacial lattice and orbital reconstructions [3]. Since there is no chemical substitution involved, the interfacial phases are expected to be in a “clean” limit, allowing an alternative procedure to investigate the true phase diagram of compounds in the absence of disordering tendencies.

Among the dominant issues in this field is the influence of “polar discontinuities” on charge transfer. Certain compounds employed in heterostructures, such as ${LaAlO}_{3}$ , are “polar” from the ionic perspective since they are formed by stacking $(LaO)^{+}$ and $({AlO}_{2})^{-}$ layers. This stacking of layers can be easily seen to be unstable. From elementary electromagnetic theory it is known that a layer with a uniform charge density produces an electrostatic potential that grows linearly away from the layer. For oppositely charged layers separated by a small distance, the electrostatic potential has a linear dependence in between but, more importantly, a different constant value on either side. Imagine now that we bring together $N$ double layers: the difference in the potential between the left and right side of this ensemble will grow like $N$ . In the bulk limit, where $N$ diverges, so does the energy. Therefore, a configuration of layers $+ 1$ , $- 1$ , $+ 1$ , $- 1$ , …, $+ 1$ , $- 1$ , $+ 1$ , $- 1$ (where $+ 1$ and $- 1$ denote the sign and charge density) cannot be stable for large $N$ .

How does the system solve this problem? The answer is that, at an interface, charge can redistribute itself to avoid the divergence or, alternatively, surface atoms can reconstruct via deviations from stoichiometry and relaxation. Consider the example of an odd number of layers, with charge distribution $+ 1 / 2$ , $- 1$ , $+ 1$ , $- 1$ , $+ 1 / 2$ . This arrangement, achieved either by surface or electronic reconstruction, is charge neutral and presents no difference between the (constant) potential on either side of the ensemble. Intuitively, this is also true for an arbitrary (odd) number of $+ 1$ and $- 1$ layers sandwiched between the two $+ 1 / 2$ layers since the system is invariant under reflections with respect to the center, implying that the potential on either side has to be the same. On the other hand, the configuration described in the previous paragraph involving only perfect double layers $+ 1$ $- 1$ is not invariant under reflections, thus allowing for the divergence problem already described.

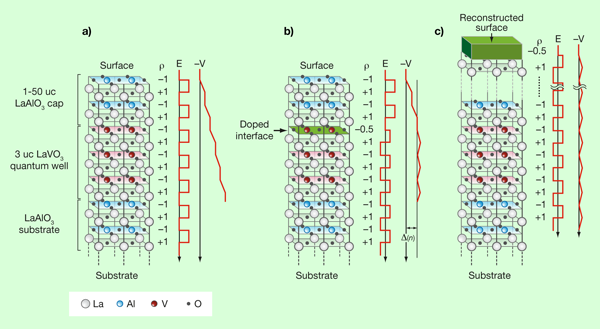
Higuchi et al. [2] have shed new light on the issue of “polar discontinuities” by using an interesting ${LaAlO}_{3} / {LaVO}_{3} / {LaAlO}_{3}$ configuration, as sketched in Fig. 1(a). The first group of ${LaAlO}_{3}$ layers is grown over a substrate and can be considered to be very thick for all practical purposes. Over the initial ${LaAlO}_{3}$ layers, a relatively small number of ${LaVO}_{3}$ layers are grown. This is followed by another small set of ${LaAlO}_{3}$ layers acting as a cap for the full structure. Note that ${LaVO}_{3}$ has the same polar structure as ${LaAlO}_{3}$ , involving $(LaO)^{+}$ and $({VO}_{2})^{-}$ layers. Thus, in the absence of surface or electronic reconstruction, the previously explained divergence of the electrostatic potential will occur, as sketched in Fig. 1(a).

However, in this structure, Higuchi et al. have observed a very interesting competition that solves this divergence problem. When the capping ${LaAlO}_{3}$ layers are thick enough, the way to avoid the diverging electrostatic potential is as it was described before; namely, the first layer (surface) reduces its charge by half via surface reconstruction and the potential does not grow anymore when moving deeper into the sample [Fig. 1(c)]. However, Higuchi et al. have observed a second intriguing possibility when the capping ${LaAlO}_{3}$ is thin. In this case, it may be energetically favorable to create the $- 1 / 2$ layer inside the ${LaVO}_{3}$ region, as opposed to the surface of the entire system, as shown in Fig. 1(b). In this configuration, there is still an energy penalization due to the increase of the potential caused by the unreconstructed capping ${LaAlO}_{3}$ layers, but it may occur that reducing the charge in the top layer of ${LaVO}_{3}$ could still be energetically less costly than the atomic reconstruction at the ${LaAlO}_{3}$ surface. Then, a competition could exist: by varying the number of capping ${LaAlO}_{3}$ layers a transition may be observed between two different regimes of transport properties, since having the charge-modified layer either at the surface or inside the “well” defined by the ${LaVO}_{3}$ layers can induce substantial differences in transport. This effect has been indeed observed experimentally in the interesting seminal work of Higuchi et al. using resistance and Seebeck coefficient measurements.

This line of research provides a novel direction for oxide heterostructures. Via the preparation of systems involving three regions, two of them thin, charge doping of the middle thin region can be achieved and different regimes of transport can be observed. This geometry illustrates the dramatic importance that the polar discontinuity can have: in the specific case studied by Higuchi et al. the electronic charge doping of the ${LaVO}_{3}$ internal layers was achieved by controlling the number of ${LaAlO}_{3}$ top layers. These results will certainly contribute to the design of future oxide heterostructures where carrier doping of materials will be obtained without following the standard, and disordering, chemical substitution procedure.

Acknowledgements

This research is supported by the NSF Grant No. DMR-0706020, and the Div. of Materials Sciences and Eng., U.S. DOE under contract with UT-Batelle, LLC.

References

E. Dagotto, Science 309, 257 (2005)
T. Higuchi, Y. Hotta, T. Susaki, A. Fujimori, and H. Y. Hwang, Phys. Rev. B 79, 075415 (2009)
For a quick overview of the subject see the Perspective articles written by H. Hwang, Science 313, 1895 (2006); and E. Dagotto, 318, 1076 (2007)
A. P. Ramirez, Science 315, 1377 (2007)

About the Author

Elbio Dagotto is a Distinguished Professor of Physics at the University of Tennesse and Distinguished Scientist at the Materials Science and Technology Division of Oak Ridge National Laboratory. He received his Ph.D. in Physics in 1985 at the Instituto Balseiro, Bariloche, Argentina. Dagotto has been working mainly on computational studies of models for systems where strong correlations among the electrons play an important role. He is a Fellow of the American Physical Society, a member of the Solid State Sciences Committee of the National Academy of Sciences, and a former divisional editor of Physical Review Letters (1998–2002). Dr. Dagotto was named an Outstanding Referee by the American Physical Society in 2008.