A view from the edge

H. A. Fertig

Viewpoint

A view from the edge

Department of Physics, Indiana University, Bloomington, IN 47405

February 23, 2009• Physics 2, 15

Measurements of the heat transport at the edges of two-dimensional electron systems appear to provide explanations about the quantum Hall state that have not been forthcoming via charge transport experiments.

Figure caption — **Figure 1:** (a) Energy spectrum of a clean integer quantum Hall system as a function of guiding center position $X$ . States near the edges disperse and carry current. By filling them to different Fermi energies $E_{F}^{(L)}$ and $E_{F}^{(R)}$ , a net current flows down the sample which yields a quantized Hall resistance $R_{H}$ . (b) Interpretation in terms of classical orbits: In bulk, electrons orbit around a fixed position and do not carry current. At the edges specular reflection induces current-carrying motion.

Charged particles tend to undergo circular motion in a magnetic field. The trapping of such particles by magnetic field lines plays a key role in a host of physical phenomena, from protecting the planet from harmful radiation to the confinement of plasmas in fusion experiments. At much lower energies than these examples, quantum mechanics introduces a remarkable range of phenomena, particularly for electrons confined to two dimensions in a perpendicular magnetic field. Here the classical orbits described above become quantized with microscopically small radii of approximately $10 nm$ in a $10 T$ magnetic field. With electrons pinned to such small areas, one might expect that such systems would be rather poor conductors. However, the most basic observation in this system is the quantum Hall effect, where for sufficiently clean and cold samples one may pass a current $I$ between two contacts, and observe a voltage drop $V_{H}$ essentially perpendicular to the current flow, such that the Hall resistance $R_{H} = V_{H} / I$ takes the form of $h / e^{2} N$ , with $N$ an integer (integer quantized Hall effect) or a rational fraction (fractional quantized Hall effect), independent of the details of the sample geometry.

In such systems edges play a crucial role, where persistent local currents lead to the quantization of the Hall effect. This extremely precise quantization, however, limits how much may be learned from charge transport at the edge. But now a new type of measurement, reported in Physical Review Letters by G. Granger, J. P. Eisenstein, and J. L. Reno at Caltech, involving heat transport at the edge, may provide new insight [1].

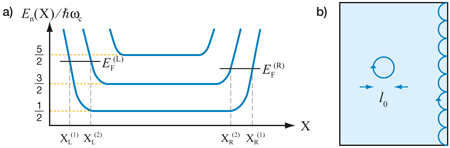
A resolution of the seeming paradox of the existence of persistent currents despite the pinning of electrons by the magnetic field was introduced by Bert Halperin years ago [2]. In an idealized situation where a sample is very clean, one can solve the Schrödinger equation for the system in the presence of an edge. The wave functions are extended parallel to the edge but are confined around a positional quantum number $X$ , called the guiding center coordinate, perpendicular to the edge. States far from the edge have a simple harmonic oscillator spectrum with discrete energy levels called Landau levels. The separation between allowed values of $X$ is tiny and so there is a huge number of allowed states for each Landau level $n$ .

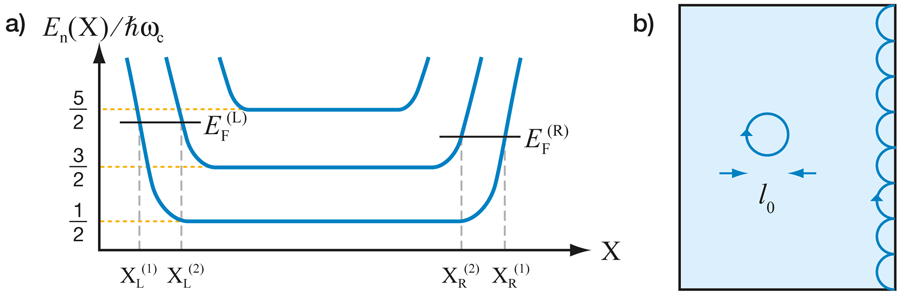
The energies of states with guiding center closer to the edge deviate from the bulk value, generally increasing as $X$ approaches the edge [see Fig. 1(a)]. Classically, this corresponds to skipping trajectories involving specular reflection of the electrons [Fig. 1(b)], allowing their transport down the length of the system. Thus each edge carries a current, even in equilibrium, and these currents are chiral; they have a unique direction determined only by the relative orientation of the magnetic field and the edge itself.

The edge currents have a number of remarkable properties. Because there is a large gap between the Fermi energy and states in the bulk, disorder cannot admix the edge states with states deeper in the sample such that current might leak away from an edge. Moreover, the chirality of the edge states guarantees that neither disorder nor roughness at the edge will backscatter edge electrons, as would happen in more standard one-dimensional systems [3]. Thus the Hall currents, and the quantized Hall effect, are very robust, provided the Fermi energy is well inside a gap between Landau levels in the bulk [2]. Clear evidence for these chiral edge currents has been found in experiment, for example, in careful studies of the Hall currents as a function of sample width [4], or by detecting the magnetic moment associated with them [5].

Edge states play a crucial role in the thermodynamics of the quantum Hall system at low temperatures: they are the only gapless excitations available in the system, at least in the clean limit. These excitations are formed by exciting electrons from just below the Fermi energy at an edge to just above [see Fig. 1(a)], and can have arbitrarily low energy, so they are important at any temperature, no matter how small. The actual occupation of the guiding center states for integer quantum Hall states follows a Fermi-Dirac distribution in equilibrium. This is very difficult to detect through charge transport because of the robustness of the total current, which is nearly unaffected for temperatures well below the bulk gap.

Granger and coauthors have developed a method for probing this property of the edge states. Using very small contacts laid out around the system edges, they injected electrons at a higher temperature than the system bulk, and measured the local electron temperature a distance away from the injection point. The result was that the electrons were warmer than the bulk electrons on only one side of the injection point, down the direction that the hot electrons should be carried by the edge current. This constitutes one of the most direct experimental demonstrations of chiral edge currents to date.

This new method is promising in that it probes properties near the quantum Hall edge that are inaccessible in charge transport experiments. The cooling of the electrons along the edge must involve inelastic processes, including coupling with lattice phonons and localized electron states in the bulk. For the $N = 1$ quantized Hall effect there are thought to be exotic, gapless collective excitations involving spin textures [6], to which charge transport is insensitive but heat transport may couple. There are also situations in the fractional quantized Hall regime in which several edge states may carry currents in different directions at the same edge; such counterpropagating modes have not been observed in charge transport, most likely due to the effects of disorder when states of opposite chirality are proximate to one another [3,7].

The fractional quantum Hall edge is more complicated than its integer counterpart; it cannot be described in terms of single particle physics, and is best described in terms of a correlated state known as a Luttinger liquid [8]. One possible explanation of the missing counterpropagating modes is that disorder restructures the edge modes into a single charged forward propagating mode and one or more neutral counterpropagating modes [9]. Experiments that measure charge transport do not appear to be sensitive to the latter. But neutral modes carry energy, and may be detectable in thermal transport.

In principle such experiments could open a long-sought window on fractional quantum Hall states. These highly correlated states have subtle topological properties that can be distinguished by their edge state structure [10]. In real disordered samples these are likely to carry only a single charged mode [7] so that detection of neutral modes will be needed to learn about their edge state structure. Such measurements could also provide insight into fractional quantum Hall states involving pairing [11] or larger clustering of electrons that are at the heart of proposals to realize topological quantum computation [12].

While the robustness of charge transport at the quantum Hall edge yields up the beauty of precise quantization of the Hall resistance, it limits what can be learned from it. The observation of chiral heat transport offers a new and potentially exciting window into the low-energy physics of the quantum Hall system.

References

G. Granger, J. P. Eisenstein, and J. L. Reno, Phys. Rev. Lett. 102, 086803 (2009)
B. I. Halperin, Phys. Rev. B 25, 2185 (1982)
T. Giamarchi, Quantum Physics in One Dimension (Oxford, New York, 2004)[Amazon][WorldCat]
B. E. Kane, D. C. Tsui, and G. Weimann, Phys. Rev. Lett. 59, 1353 (1987)
E. Yahel, D. Orgad, A. Palevski, and H. Shtrikman, Phys. Rev. Lett. 76, 2149 (1996)
R. Côté et al., Phys. Rev. Lett. 78, 4825 (1997)
C. L. Kane and M. P. A. Fisher, Phys. Rev. B 51, 13449 (1995)
X. G. Wen, Phys. Rev. B 41, 12838 (1990)
C. L. Kane, M. P. A. Fisher, and J. Polchinski, Phys. Rev. Lett. 72, 4129 (1994)
X. G. Wen, Adv. Phys. 44, 405 (1995)
G. Moore and N. Read, Nucl. Phys. B 360, 362 (1991)
C. Nayak et al., Rev. Mod. Phys. 80, 1083 (2008)

About the Author

Herbert Fertig is a Professor of Physics at Indiana University in Bloomington. He received his undergraduate degree from Princeton University and his Ph.D. from Harvard University under the direction of Bert Halperin in 1988. After a postdoctoral fellowship with Sankar Das Sarma at the University of Maryland, he joined the faculty of the University of Kentucky in 1991, moving to Indiana in 2004. Professor Fertig was elected a Fellow of the American Physical Society in 2001, was chosen as a Lady Davis Fellow for 2006–7, and in 2008, he was recognized as an Outstanding Referee for the Physical Review journals. His research focuses mostly on low-dimensional electron systems, with particular interests in quantum Hall effects, and recently on graphene.