Cloaking at a distance

Thomas Philbin

Viewpoint

Cloaking at a distance

Thomas Philbin

School of Physics and Astronomy, University of St Andrews, North Haugh, St Andrews, Fife KY16 9SS, Scotland, UK

March 2, 2009• Physics 2, 17

A proposal for a new type of cloaking device suggests a way to hide both a distant object and the cloak itself.

Figure caption — **Figure 1:** (a) The slab of empty space $0 < x < L$ is optically cancelled by a slab of negative-index material in $- L < x < 0$ . (b) The same cancellation effect works with an object in $0 < x < L$ , if the negative-index slab contains an anti-object. (c) A spherical shell $b < r < c$ is optically cancelled by a negative-index shell $a < r < b$ . If the core $r < a$ is optically equivalent to a sphere of radius $c$ , then this device is invisible. (d) The same as (c) but with an object in the cancelled shell $b < r < c$ . The object is cloaked: both it and the cloaking sphere are invisible.

Electromagnetic cloaking devices that render objects invisible are now an active research subject, a development that has understandably aroused considerable interest among researchers, the military, and the general public. The basic idea of cloaking is a device that guides incoming light around an interior region such that the light emerges as if it had propagated through empty space; any object in the interior region is thereby rendered invisible. In a paper appearing in Physical Review Letters, Yun Lai and colleagues at the Hong Kong University of Science and Technology present a theoretical design for cloaking that is far less intuitive than this simple picture [1]. In their design, the object to be hidden is placed at a specific position in the vicinity of a new type of cloaking device that is tailor-made for the object. At this position, and only at this position, both object and cloak become invisible. In practice, this “cloaking at a distance” would be severely limited, but it is another example of how geometrical ideas can reveal strange possibilities.

The original cloaking recipes [2,3] used coordinate transformations of Maxwell’s equations as a design tool. In simple terms: they introduced a material medium that, as regards electromagnetism, makes light bend in a curved path around a “hole.” The path that the light follows is the same that would be expected if Maxwell’s equations were transformed to a different coordinate system. Anything placed in this hole is inaccessible to electromagnetism and thus is hidden, but if the transformation ultimately maps the coordinate system back to itself at some distance from the hole, then the solutions beyond that distance are the same as if the material were not there—the material (cloak), the hole, and anything inside the hole are invisible.

Mathematically, the coordinate transformation produces a singularity, which in real space shows up as an infinite phase velocity for the light at the boundary of the hole. Phase velocities faster than the speed of light in vacuum are possible, but only in dispersive materials where the optical behavior changes significantly with frequency. In practice, these severe demands mean that the cloak will only operate at a single frequency and in the first experimental realization of this idea, the cloak worked only at a microwave frequency [4]. More recently, theorists have figured out ways to overcome the need for infinite phase velocities [5].

In the last few years, Graeme Milton, Nicolae Nicorovici, and collaborators [6–8] have studied a type of cloaking at a distance where point dipoles outside of the cloak are hidden. In contrast, Lai et al.’s new theory works for objects of arbitrary size and shape [1]. Their approach to cloaking again exploits the equivalence between making a coordinate transformation and introducing a certain type of optical material. In this case, the transformation is a folding of a spatial coordinate back on itself, for example $x \to x^{'} = - x$ . This kind of transformation is equivalent [9] to introducing a medium with a negative refractive index (sometimes called left-handed media) in which an entering light ray is bent (refracted) in the “wrong direction.” The classic example [10] corresponds to the simple transformation above and gives permittivity and permeability $ε^{'} = μ^{'} = - 1$ (in empty space $ε = μ = 1$ ), but a general folding transformation will give negative $ε^{'}$ and $μ^{'}$ that vary in space.

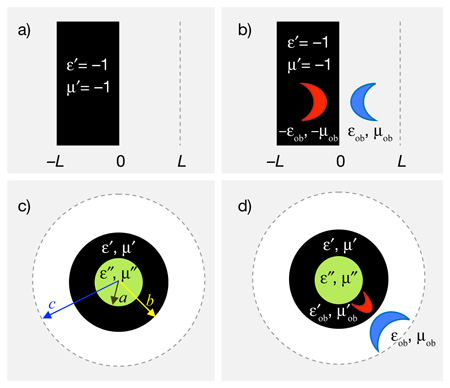
In a medium of refractive index $n$ , light experiences a distance $s$ as an effective distance—called an optical path length—given by $n s$ . Thus a transformation that folds back on itself gives rise to a negative optical path length. To see that the optical path length is negative, consider the transformation $x^{'} = - x$ , applied to the region $0 < x < L$ in Fig. 1(a). This folds $x = L$ back onto $x = - L$ , so these two planes become optically equivalent. The region $- L < x < 0$ of overlap is exactly equivalent to a material with $ε^{'} = μ^{'} = - 1$ , which cancels out a slab of empty space of the same thickness [9]: As light moves from $0$ to $- L$ the negative-index material “undoes” the propagation from $L$ to $0$ so that the light ends up exactly as it was at $L$ .

This optical cancellation property of the folding transformation can also be used to cancel an object. Consider an object, with permittivity $ε_{o b}$ and permeability $μ_{o b}$ , within a distance $L$ from the same slab [Fig. 1(b)]. The transformation $x^{'} = - x$ in the region $0 < x < L$ gives a negative-index slab as before, but the transformation of Maxwell’s equations in the object produces an effective material with permittivity $- ε_{o b}$ and permeability $- μ_{o b}$ , as shown in [Fig. 1(b)]. The cancellation argument holds as before, so we now have a left-handed slab that will optically cancel a slab of empty space containing the object. The part of the slab with permittivity $- ε_{o b}$ and permeability $- μ_{o b}$ functions as an “anti-object”.

In their description of cloaking at a distance, Lai et al. switch to spherical coordinates and perform the folding transformation on the radial coordinate. Figure 1(c) shows how one can design a cloak that optically cancels a spherical shell of empty space. The transformation folds the shell $b < r < c$ onto the shell $a < r < b$ , meaning space is also compressed in the transformation. This results in an inhomogeneous shell with negative $ε^{'}$ and $μ^{'}$ . The region from $r = a$ to $r = c$ now has zero optical length, but for cloaking we require something that behaves optically like empty space, not like the absence of space. This is remedied by filling the central core $r < a$ with a material of permittivity $ε^{''}$ and permeability $μ^{''}$ that has the optical path length of an empty sphere of radius $c$ . The device now behaves optically as empty space and is therefore invisible. Finally, we can imagine placing an object in the empty shell $b < r < c$ and use the folding transformation to obtain an anti-object in the left-handed shell [Fig. 1(d)]. The object and the sphere are now invisible, provided the actual object is placed in the exact location where it is mapped onto the anti-object by the folding transformation.

Lai et al. [1] have confirmed their design by numerical simulations. A more conventional description of this cloaking effect is that the scattered light from the object and the device interfere destructively. But this conventional picture has its own cloaking effect: it completely hides the simple geometry operating behind the scenes.

The cloaking recipe described here only works in a stationary regime, where the light can explore and adjust to the entire region of cloak plus object: there is no spooky action at a distance. Moreover, this effect could only be implemented in a very limited way. Left-handed media can be constructed using modern metamaterials [11], but a given device functions only in a narrow bandwidth and losses are a major problem. Nevertheless, the work described here is another example of how clever thinking about geometry and new materials are inspiring a new approach to optics (see [12] for a review). While the major practical impact of these developments will probably be in rather mundane devices, the full richness of this new terrain needs to be explored. Even in the 21st century, classical optics still has some magic left.

References

Y. Lai, H. Chen, Z-Q. Zhang, and C. T. Chan, Phys. Rev. Lett. 102, 093901 (2009)
U. Leonhardt, Science 312, 1777 (2006)
J. B. Pendry, D. Schurig, and D. R. Smith, Science 312, 1780 (2006)
D. Schurig, J. J. Mock, B. J. Justice, S. A. Cummer, J. B. Pendry, A. F. Starr, and D. R. Smith, Science 314, 977 (2006)
U. Leonhardt and T. Tyc, Science 323, 110 (2009)
G. W. Milton and N. A. P. Nicorovici, Proc. R. Soc. A 462, 3027 (2006)
N. A. P. Nicorovici, G. W. Milton, R. C. McPhedran, and L. C. Botten, Opt. Express 15, 6314 (2007)
G. W. Milton, N. A. P. Nicorovici, R. C. McPhedran, K. Cherednichenko, and Z. Jacob, New. J. Phys. 10, 115021 (2008)
U. Leonhardt and T. G. Philbin, New J. Phys. 8, 247 (2006)
V. G. Veselago, Sov. Phys. Usp. 10, 509 (1968)
A. K. Sarychev and V. M. Shalaev, Electrodynamics of Metamaterials (World Scientific, 2007)[Amazon][WorldCat]
U. Leonhardt and T. G. Philbin, arXiv:0805.4778; Prog. Optics (to be published)

About the Author

Thomas Philbin completed his research degrees at Trinity College Dublin and the National University of Ireland. He later held postdoctoral appointments at the University of St Andrews in Scotland, the Max Planck Institute in Erlangen, Germany, and the National University of Singapore. He currently holds a Royal Society of Edinburgh/Scottish Government Personal Research Fellowship at St Andrews. His current research interests are Casimir forces, artificial black holes, and uses of differential geometry in optics.