Peaceful coexistence of nuclear shapes

Paul Mantica

Viewpoint

Peaceful coexistence of nuclear shapes

National Superconducting Cyclotron Laboratory, Michigan State University, East Lansing, MI 48824, USA

March 2, 2009• Physics 2, 18

Experiments show that spherical and nonspherical states of a light nucleus near neutron number 28 coexist at the same energy, challenging the usefulness of the notion of stable and persistent “magic numbers.”

Figure caption — **Figure 1:** Schematic illustration of the low-energy structure of $^{43} S$ . Energy is increasing along the vertical axis, and the horizontal axis represents the extent of nuclear deformation (represented by a parameter $β$ ). Positive $β$ values correspond to prolate (football) shapes, negative values to oblate (pancake) shapes, and $β = 0$ represents a spherical shape. The deformed band structure is taken from [6]. The linewidths of the transitions from the two $7 / 2 -$ levels to the ground state qualitatively represent the difference in transition rates for these decays. The existence of both a spherical state and a deformed state at low energy indicates the collapse of the shell gap at neutron number 28, as confirmed by the measurements of Gaudefroy *et al.* [1].

Some of the most basic tenets of nuclear science have fallen victim to new experimental findings in nuclei with extreme neutron-to-proton ratios, also referred to as rare isotopes. One of these tenets, the existence and persistence of the so-called “magic numbers” has been put to test by recent measurements of light nuclei with a neutron number in the vicinity of 28, where a spherical shape is expected. Gaudefroy and collaborators [1] have unambiguously determined the spin and magnetic moment of an isomeric state in $^{43} S$ , which has neutron number 27. Their results firmly establish the coexistence in $^{43} S$ of spherical and deformed shapes already known in heavier nuclei and suggest a collapse of neutron number 28 as a magic number for neutron-rich nuclei. The disappearance of the neutron number 28 as a magic number is attributed to a reduction in the energy spacing between adjacent quantum mechanic states of the nucleus, and reiterates the need to broadly examine the robustness of the magic numbers across the nuclear chart. Such an ambitious and important activity will require investments in the next generation of rare isotope beam production facilities.

One of the outstanding questions in nuclear science is the evolution of shell structure from what is known in the region of the stable isotopes. The nuclear shell model was developed based on empirical data within a limited region of the nuclear chart nearest the stable isotopes, where nuclei with certain proton and neutron numbers exhibited properties consistent with extra nuclear binding energy. This added stability at proton and neutron numbers 2, 8, 20, 28, 50, and 82, as well as neutron number 126, was attributed to large energy gaps between successive shell model orbits.

The notion that these magic numbers extend across the entire nuclear chart has been seriously challenged in recent years. As an example, the shell gap at neutron number 20 is well established in stable $^{40} Ca$ , but is eroded in $^{32} Mg$ . The $^{32} Mg$ nucleus is eight protons removed from $^{40} Ca$ and exhibits a low-energy quantum structure, better attributed to a deformed shape defined by the collective motion of many nucleons. Indeed, the nucleus $^{34} Si$ , which has just two protons more than $^{32} Mg$ , has a low-energy structure more consistent with $^{40} Ca$ and a quasispherical shape.

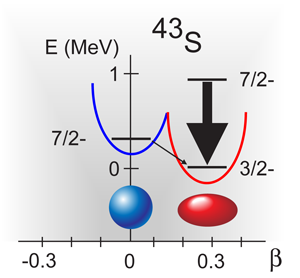
Transitions from spherical to deformed nuclei occur across the nuclear landscape. These transitions are often sudden, as in the case described above for the neutron-rich nuclei having 20 neutrons. However, an intermediate condition of shape coexistence is also possible. Shape coexistence is denoted by a near degeneracy of different shapes. The nucleus is an important and unique laboratory to examine the quantum underpinnings of shape coexistence, since the nucleus can exhibit structures associated with both single-nucleon and collective motion. One sign of shapes coexisting at low energy in atomic nuclei is an increased energy level density, which happens simply from the need to accommodate distinct structures at nearly the same nuclear excitation energy.

Another observable is the presence of nuclear levels with unique parity. The major shells in the energy spectrum derived from the shell model have a clustering of orbits with like parity. The reduction of the shell energy gaps and onset of deformation can bring orbits with opposite parity into close proximity. Nuclear shape coexistence can also lead to nuclear isomerism, where photon emission from a given state is hindered due to decay energy or incompatibility with potential final states. The systematic variation of level structures as a function of the neutron-to-proton ratio can reveal shape coexistence. However, detailed measurements of the properties of the low-energy nuclear states are needed to disentangle and distinguish the coexisting shapes.

The magnetic dipole moment is an important nuclear property that can be used to identify and characterize shape coexisting structures. The magnetic moment is sensitive to the orbital and spin contributions to the nuclear state. Therefore, a measurement of the magnetic moment indicates the shell model character of the state. The sign of the magnetic moment on its own provides critical insight into the composition of a nuclear state, because of the sign difference between the free proton ( $+ 2.79$ nuclear magnetons) and free neutron ( $- 1.91$ nuclear magnetons) magnetic moments. Deviations in magnetic moment values from shell model expectations usually indicate the mixing of many shell model orbits, and the onset of deformation. The magnetic moment is an excellent probe of both collective and single-particle nuclear motion. In practice, magnetic moments are deduced from a direct measurement of the nuclear $g$ factor, which is the ratio of the magnetic moment and the nuclear spin. The measurement of $g$ factors in a nucleus that exhibits shape coexistence is one method to isolate competing shapes.

Erosion of the shell gap at neutron number 20 in neutron-rich $^{32} Mg$ has been well documented, as discussed above. The robustness of the shell gap at neutron number 28 in neutron-rich nuclei, however, is under debate. The low-energy structure of $^{48} Ca$ exhibits features of a shell closure at neutron number 28 and spherical shape for this neutron-rich, stable nuclide. Disparate views abound on the nature of the neutron number 28 shell closure at $^{42} Si$ , which is six protons removed from $^{48} Ca$ . The beta-decay half-life [2] and low-energy-level structure of $^{42} Si$ , [3] suggest that this nuclide has a well-deformed ground state, and therefore that the shell gap at neutron number 28 is dissolved. However, a substantial energy gap between shell model orbits at atomic number 14, which would strongly hinder development of collective features along neutron number 28, has been proposed for $^{42} Si$ , [4]. Examination of nuclei in the transition region between $^{48} Ca$ and $^{42} Si$ , may offer a means to resolve the outstanding questions regarding the evolution of the neutron number 28 shell gap. For example, an isomeric state was identified at energy $\sim 320 keV$ in $^{43} S$ [5], and cited as possible evidence for the coexistence of spherical and deformed structures near neutron number 28.

Gaudefroy et al. [1] have deduced both the sign and magnitude of the $g$ factor for the known isomeric state in $^{43} S$ to be $- 0.317$ $+ / - 0.004$ . The measurement was completed using the Time Dependent Perturbed Angular Distribution (TDPAD) method, where the spin precession of a nuclear state in a static magnetic field is monitored via photon emission. The emitted photon has a fixed angular momentum and orientation, leading to a distinct emission pattern. In a TDPAD measurement, the photon intensity oscillates with time, similar to the observation of the beacon of a lighthouse at a remote, fixed position. The oscillation frequency and phase of the photon intensity are related to the magnitude and sign of the $g$ factor, respectively. Agreement between shell model theory and experiment for the $g$ factor suggests that the isomeric state has quasispherical shape.

An additional outcome of the work by Gaudefroy et al. is a more precise measurement of the half-life of $415 + / - 5 ns$ for the isomeric state in $^{43} S$ . The high precision of the half-life defines the characteristics of the hindered photon transition between the isomer and ground states, restricting the spin and parity of the ground state to $3 / 2 -$ . Neutron excitations across the neutron number 28 energy gap explain the structure of the $^{43} S$ ground state, and are only plausible if this shell gap is reduced and nuclear deformation is present (Fig. 1). The second $7 / 2 -$ level at $\sim 940 keV$ already known in $^{43} S$ depopulates rapidly to the deformed $3 / 2 -$ ground state [6], in contrast to the slow transition rate associated with the decay of the spherical $7 / 2 -$ isomeric state. The new results for the $g$ factor and half-life of the isomeric state at $\sim 320 keV$ in $^{43} S$ provide direct evidence on the presence of coexisting and distinct spherical and deformed structures in $^{43} S$ and the collapse of the shell gap at neutron number 28 for neutron-rich nuclei.

The presence of both a spherical isomeric state and a deformed band structure at low-energy in $^{43} S$ indicates that the neutron number 28 shell gap is significantly reduced in neutron-rich nuclei. Erosion of the shell gaps at both neutron numbers 20 and 28 in neutron-rich nuclei does not support the naive expectation that the proton and neutron magic numbers established in stable nuclei extend to the limits of the nuclear chart. The evolution of the shell gaps far from the stable isotopes is critical to the development of nuclear structure theories, such as the shell model, that rely on empirical data to account for shortcomings in the nuclear Hamiltonian via effective interactions. The disappearance of shell gaps also impacts modeling efforts in nuclear astrophysics. The properties of neutron-rich nuclei are critical input parameters to simulate mass processing along the astrophysical rapid neutron capture pathway, yet are governed by the location of shell gaps at neutron numbers 50 and 126.

Studying the evolution of the shell gaps above neutron number 28, however, will be extremely challenging. First signs for the collapse of the shell gaps at neutron numbers 20 and 28 were seen in nuclei with neutron-to-proton numbers exceeding 1.6:1. Access to nuclei with such extreme ratios was only possible with advances in isotope production and selectivity, along with the development of highly sensitive experimental detection systems. Strategic investments in advanced rare isotope production facilities, like the proposed Facility for Rare Isotope Beams in the United States, will provide the necessary tools to explore shell evolution at the extremes of the nuclear chart and develop a comprehensive and predictive theory of nuclear structure.

References

L. Gaudefroy et al., Phys. Rev. Lett. 102, 092501 (2009)
S. Grévy et al., Phys. Lett. B 594, 252 (2004)
B. Bastin et al., Phys. Rev. Lett. 99, 022503 (2007)
J. Fridmann et al., Nature 435, 922 (2005)
F. Sarazin et al., Phys. Rev. Lett. 84, 5062 (2000)
R. W. Ibbotson et al., Phys. Rev. C 59, 642 (1999)

About the Author

Paul Mantica is a Professor at Michigan State University with appointments in the Department of Chemistry and National Superconducting Cyclotron Laboratory (NSCL). He received his Ph.D. in Nuclear Chemistry in 1990 from the University of Maryland. Mantica has been studying the ground state properties of rare isotopes for more than 20 years, and his present research activities involving measuring beta-decay properties and nuclear moments of short-lived radionuclides. He is presently Department Head of the Experimental Nuclear Science Group at NSCL, and serves as the National Director of the Nuclear and Radiochemistry Summer Schools, which are sponsored by the American Chemical Society and the U.S. Department of Energy.

Shell Erosion and Shape Coexistence in ${}_{16}^{43}S_{27}$

L. Gaudefroy, J. M. Daugas, M. Hass, S. Grévy, Ch. Stodel, J. C. Thomas, L. Perrot, M. Girod, B. Rossé, J. C. Angélique, D. L. Balabanski, E. Fiori, C. Force, G. Georgiev, D. Kameda, V. Kumar, R. L. Lozeva, I. Matea, V. Méot, P. Morel, B. S. Nara Singh, F. Nowacki, and G. Simpson

Phys. Rev. Lett. 102, 092501 (2009)

Published March 2, 2009

Read PDF