An astronomical solution to an old quantum problem
In 1926, shortly after Erwin Schrödinger had proposed his wave equation that launched the era of modern quantum mechanics, he and Hendrik Lorentz were puzzling whether there were wave packet solutions of the equation that described localized particles traveling in elliptical orbits like the particles of classical mechanics and of Bohr’s old quantum mechanics [1]. They concluded that there were no such solutions because the wave equation is dispersive for the atomic Coulomb potential and thus any initially localized wave packet will inevitably spread around the orbit. Indeed there have been a series of experiments by a number of groups since the mid-1980’s demonstrating exactly this spreading of the electron wave packets. These experiments showed in fact that the wave packets spread all the way around the orbits and coherently interfere with themselves, producing elaborate patterns of revivals and fractional revivals of the original wave packet [2].
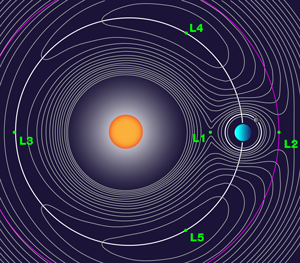
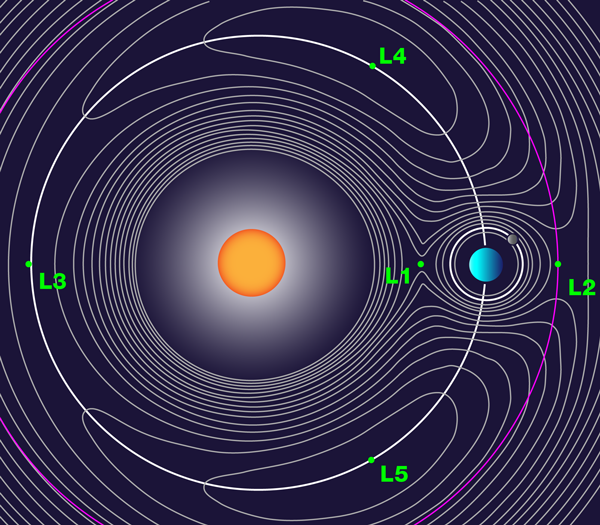
Now, in results reported in Physical Review Letters, H. Maeda (Japan Science and Technology Agency, Tokyo), J. H. Gurian, and T. F. Gallagher (University of Virginia) have beautifully demonstrated in the laboratory a solution to this problem of the spreading atomic electron wave packet using a trick that was discovered in astronomy long before the problem arose in quantum theory [3]. When a small satellite moves in a sun-earth system there are five stable points at which the satellite remains fixed with respect to the rotating sun-earth system (Fig. 1). These are the famous Lagrange L points. In 1994 Bialynicki-Birula et al. showed that stable Lagrange points could be produced in the atomic electron problem by applying a circularly polarized microwave field rotating in synchrony with an electron wave packet in a highly excited state (a so-called Rydberg atom) [4]. The electron wave packet then remains localized near the Lagrange point while circling the nucleus indefinitely. Effectively the atom is made to behave quite classically.
One of the fundamental assumptions in quantum mechanics is the correspondence principle, formulated by Niels Bohr [5]. It states that quantum mechanics must reduce to classical mechanics in the “macroscopic” limit. The definition of macroscopic in the case of wave packets is not so clear. In fact, in the case of ordinary Rydberg wave packets the series of decays and revivals is a signature of the quantized energy structure and persists for arbitrarily highly excited atoms so long as they are not subjected to high-frequency noise. They are immune even to low-frequency noise, which simply adiabatically deforms the orbits without disturbing the orbital periods and thus the decays and revivals. The new nonspreading wave packets would at first seem to escape this problem and provide a true classical limit of a single atom. One should note, however, that the Lagrange points are actually local minima in the frame rotating with the field. The electron can then perform small oscillations (librations) about the stable point. This motion itself would be subject to quantization. One might then expect to see the effects of these quantized levels in a sufficiently well controlled experiment over quite long times. It would be quite interesting to see such effects in later experiments, in effect pushing the elusive “macroscopic” limit even further.
Of course, the astronomical problem does not have an external applied field. One might wonder whether the two-electron atom has states that are analogous to the classical Lagrange L points. The analog is not at all exact because the two electrons are of low equal mass compared to the nucleus. Furthermore, the two electrons repel each other, whereas the gravitational forces are always attractive. In spite of these distinctions there are states that are somewhat analogous. They have not been observed in the laboratory but they have been theoretically analyzed [6]. Initial experiments have been carried out with localized Rydberg wave packets in two-electron atoms, but so far only the unstable autoionizing orbits have been observed [7]. The quest of Lorentz and Schrödinger is finally being realized, if in a somewhat different form than they envisioned.
Note added (9 March 2009): Since the submission of the Maeda et al. paper another paper was submitted by Mestayer et al., and will appear in Physical Review A, reporting the stabilization of a Rydberg wave packet by a series of half-cycle pulses that periodically kick the electron. While the method has no obvious astronomical analog it effectively stabilizes the electronic wave packet over hundreds of orbits.
References
- The calculations and correspondence of Lorentz and Schrödinger concerning this question are reproduced in the bookLetters on Wave Mechanics, edited by K. Przibram (Philosophical Library, New York, 1967)[Amazon][WorldCat]
- A popular-level description of these phenomena may be found in M. Nauenberg, C. R. Stroud, Jr., and J. A. Yeazell, Scientific American 270, 44 (1994)
- H. Maeda, J. H. Gurian, and T. F. Gallagher, Phys. Rev. Lett. 102, 103001 (2009)
- I. Bialynicki-Birula, M. Kalinski, and J. H. Eberly, Phys. Rev. Lett. 73, 1777 (1994)
- N. Bohr, Zeits. f. Physik 2, 423 (1920)
- M. Kalinski, J. H. Eberly, J. A. West, and C. R. Stroud, Jr., Phys. Rev. A 67, 032503 (2003)
- S. N. Pisharody and R. R. Jones, Science 303, 813 (2004)