Classifying multiferroics: Mechanisms and effects

Electricity and magnetism were combined into one common discipline in the 19th century, culminating in the Maxwell equations. But electric and magnetic ordering in solids are most often considered separately—and usually with good reason: the electric charges of electrons and ions are responsible for the charge effects, whereas electron spins govern magnetic properties

There are, however, cases where these degrees of freedom couple strongly. For example, in the new, large field of spintronics, the effects of spins on the transport properties of solids (and vice versa) allow the possibility to control one by the other. The finding of a strong coupling of magnetic and electric degrees of freedom in insulators can be traced back to Pierre Curie, but the real beginning of this field started in 1959 with a short remark by Landau and Lifshitz in a volume of their Course of Theoretical Physics [1]:

“Let us point out two more phenomena, which, in principle, could exist. One is piezomagnetism, which consists of linear coupling between a magnetic field in a solid and a deformation (analogous to piezoelectricity). The other is a linear coupling between magnetic and electric fields in a media, which would cause, for example, a magnetization proportional to an electric field. Both these phenomena could exist for certain classes of magnetocrystalline symmetry. We will not however discuss these phenomena in more detail because it seems that till present, presumably, they have not been observed in any substance.”

The situation changed soon thereafter, when Dzyaloshinskii predicted [2], and Astrov observed [3], this type of coupling, which is now known as the linear magnetoelectric effect. This was rapidly followed by the discovery of many other compounds of this class and by a rather complete classification of possible symmetry groups allowing for the effect.

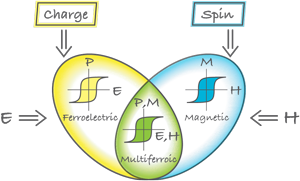
A new twist in this problem was the idea that not only can strong cross-coupling of responses exist in solids (i.e., the appearance of magnetization M in an electric field E, or the inverse effect of electric polarization P generated by the application of magnetic field H), but that there may exist systems in which two types of ordering—(ferro)magnetism, the spontaneous ordering of orbital and spin magnetic moments, and ferroelectricity, the spontaneous ordering of electric dipole moments—can coexist in one material in the absence of external electric and magnetic fields. Following Schmid [4], these materials are now called multiferroics (Fig. 1). (In principle one often includes in this category a third type of ordering, spontaneous deformation, which leads to ferroelasticity. However, nowadays what most people mean by multiferroic predominantly applies to the coexistence of magnetism and ferroelectricity.) Boracites were probably the first known multiferroics [5], and soon several others were either found in nature, or synthesized artificially [6].

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

Essentially, three events majorly revived the study of multiferroics, which had slowed down by the 70s. One was that theory began to treat the general problem of why the coexistence of magnetism and ferroelectricity is so rare [7,8]. The second and third were experimental achievements that identified two distinct classes of multiferroics.

In 2003, Ramesh’s group successfully grew thin films of one of the most popular multiferroics, ${\text{BiFeO}}_3$ [9]. The multiferroic properties of bulk ${\text{BiFeO}}_3$ are fairly weak, but in thin-film form they are greatly enhanced. The second major experimental development, also in 2003, was the discovery of a novel class of multiferroics, in which magnetism and ferroelectricity do not just coexist, but in which magnetism causes ferroelectricity. Tokura and Kimura discovered this phenomenon in ${\text{TbMnO}}_3$ [10] and Cheong found a similar effect in ${\text{TbMn}}_2{\text{O}}_5$ [11]. Since 2003, these three systems have served as test grounds (“drosophiles”) for the main physical ideas in the field.

The realization that these materials have great potential for practical applications has lead to an extremely rapid development of the field of multiferroics. Applications include the ability to address magnetic memory electrically (and without currents!), the creation of new types of 4-state logic (i.e., with both up and down polarization and up and down magnetization) and magnetoelectric sensors. If there is any doubt about the growth of this field, consider that in 2001, Nicola Spaldin organized the first special session on multiferroics at the American Physical Society’s March meeting. By 2007 there were seven of these sessions, more than double the number of sessions on the previous “hot topic”—colossal magnetoresitive manganites. The literature now contains special reviews on multiferroics [12–16], and in particular, a comprehensive discussion of different aspects of this field can be found in the collection of short review articles in Ref. [17].

To understand the basic phenomena in the field of multiferroics, and appreciate the main achievements and remaining problems in this field, it is necessary to classify multiferroics by the microscopic mechanism that determines their properties. The first part of this article is therefore devoted to this classification. In the second part of the article, we explore theoretical and practical ideas that are emerging from the different mechanisms underlying multiferroic behavior.

The microscopic origin of magnetism is basically the same in all magnets: it is the presence of localized electrons, mostly in the partially filled $d$ or $f$ shells of transition-metal or rare-earth ions, which have a corresponding localized spin, or magnetic moment. Exchange interactions between the localized moments lead to magnetic order. The situation with ferroelectrics is quite different. There are several different microscopic sources of ferroelectricity, and accordingly one can have different types of multiferroics. Generally speaking, there are two groups of multiferroics. The first group, which can be called type-I multiferroics, contains those materials in which ferroelectricity and magnetism have different sources and appear largely independently of one another, though there is some coupling between them. In these materials, ferroelectricity typically appears at higher temperatures than magnetism, and the spontaneous polarization P is often rather large (of order $10-100\mu {\text{C/cm}}^2$). Examples are ${\text{BiFeO}}_3$ ( $T_{\text{FE}}\sim 1100\text{K},T_{\text{N}}=643\text{K},\mathbf{\text{P}}\sim 90\mu {\text{C/cm}}^2$) and ${\text{YMnO}}_3$ ( $T_{\text{FE}}\sim 914\text{K},T_{\text{N}}=76\text{K},\mathbf{\text{P}}\sim 6\mu {\text{C/cm}}^2$). The second group, which we can call type-II multiferroics, is the relatively recently discovered materials [10,11], in which magnetism causes ferroelectricity, implying a strong coupling between the two. However, the polarization in these materials is usually much smaller ( $\sim {10}^{-2}\mu {\text{C/cm}}^2$). Many groups are also investigating composite multiferroics that consist of known magnets and ferroelectrics in the form of multilayers and self-organized nanostructures [16].

In this article, I will mainly discuss the microscopic picture that is at the root of the properties of multiferroics, but for many multiferroics the symmetry considerations are indispensable, especially for type-II multiferroics. In this field they were mostly developed and successfully applied by A. B. Harris, A. Aharony, and their coworkers, see, for example, Ref. [17], No. 434202. A detailed classification of possible symmetries allowing for multiferroelectricity and magnetoelectricity is given by H. Schmidt in Ref. [17], No. 434201.

Type-I multiferroics

Type-I multiferroics are “older” and more numerous. These are often good ferroelectrics, and the critical temperatures of the magnetic and ferroelectric transitions can be well above room temperature. Unfortunately, the coupling between magnetism and ferroelectricity in these materials is usually rather weak. The materials challenge for this group of multiferroics is to keep all their positive features, but enhance this coupling. As we will see later, the opposite problem exists for type-II multiferroics.

One can single out several different subclasses of type-I multiferroics, depending on the mechanism of ferroelectricity in them. We will focus on four of the major subclasses, but there are certainly others.

Multiferroic perovskites

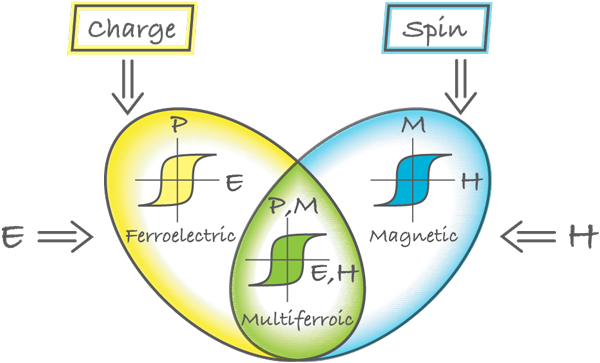
Probably the best-known ferroelectrics are the perovskites like ${\text{BaTiO}}_3$ or ${\text{Pb(ZrTi)O}}_3$ (PZT). There are many magnetic materials among perovskites [18], and also many ferroelectrics [19]. But comparing these extensive compilations, each containing more than 100 pages of tables, demonstrates that there seems to be mutual exclusion of magnetism and ferroelectricity in perovskites: there is practically no overlap of these tables. Why? Whereas for magnetism one needs partially filled $d$ shells of a transition metal, practically all ferroelectric perovskites contain transition metal ions with an empty $d$ shell, such as ${\text{Ti}}^{4+}$, ${\text{Ta}}^{5+}$, ${\text{W}}^{6+}$. Ferroelectricity in these systems is caused by the off-center shifts of the transition metal ion, which forms strong covalent bonds with one (or three) oxygens, using their empty $d$ states. And somehow, the presence of real $d$ electrons in $d^n$ configurations of magnetic transition metals suppresses this process, preventing ferroelectricity in magnetic perovskites. This so called ” $d^0$ vs $d^n$ problem” was one of the first to be studied theoretically at the beginning of the recent revival of multiferroics [7,8], and although there has been some progress, largely from ab initio calculations, still in my opinion there is no full solution of this problem [13]. The answer may well lie in the fact that this mutual exclusion is not a “theorem,” but rather a matter of numbers: in most cases a magnetic $d^n$ ion is stable in the center of its ${\text{O}}_6$ octahedra, but there may still be the cases where it is not. One possible way around this problem may be making ”mixed” perovskites with $d^0$ and $d^n$ ions, see Fig. 2(a). Unfortunately the coupling of magnetic and ferroelectric subsystems in mixed perovskites is rather weak.

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

Ferroelectricity due to lone pairs

In ${\text{BiFeO}}_3$, and probably in ${\text{BiMnO}}_3$ and ${\text{PbVO}}_3$, ${\text{Bi}}^{3+}$ and ${\text{Pb}}^{2+}$ play the major role in the origin of ferroelectricity. In these ions, there are two outer $6s$ electrons that do not participate in chemical bonds. They are called lone pairs, or sometimes dangling bonds. They have a high polarizability—the condition required for ferroelectricity in the classical description. More microscopically one can explain the origin of ferroelectricity in these compounds by ordering of these lone pairs (with certain admixture of $p$ orbitals) in one direction [Fig. 2(b)]. Apparently this is what happens in many $\text{Bi}-$ and $\text{Pb}-$containing ferroelectrics and multiferroics such as ${\text{BiFeO}}_3$, but it also helps to improve the ferroelectric properties of ${\text{Pb(Zr}}_x{\text{Ti}}_{1-x}){\text{O}}_3$.

Ferroelectricity due to charge ordering

One more mechanism that can lead to ferroelectricity and to type-I multiferroicity can be charge ordering, often observed in transition metal compounds, especially those formally containing transition metal ions with different valence. If, after charge ordering, both sites and bonds turn out to be inequivalent, this can lead to ferroelectricity [Fig. 2(c)] [20].

A corresponding mechanism can work in systems like ${\text{Pr}}_{1/2}{\text{Ca}}_{1/2}{\text{MnO}}_3$ [20] or in nickelates $R{\text{NiO}}_3$ (see Refs. [15] and [17], No. 434217) with charge ordering. But more often we meet the situation in which there exist ions with different charge (often because they are different elements), but on top of that there occurs dimerization. ${\text{TbMn}}_2{\text{O}}_5$ belongs to this class [11], as does the newly discovered multiferroic ${\text{Ca}}_3{\text{CoMnO}}_6$ [21], see below. Another similar possibility is when the bonds are inequivalent because of the structure of the material, the site-centered charge order appearing on top of that. This is the case in an organic ferroelectric ${\text{(TMTTF)}}_{2}X$ [22], and also in the multiferroic ${\text{LuFe}}_2{\text{O}}_4$ [23].

“Geometric” ferroelectricity

Lastly, we consider a case realized in, for example, ${\text{YMnO}}_3$ [24]. Ferroelectricity in ${\text{YMnO}}_3$ has nothing to do with the magnetic ${\text{Mn}}^{3+}$, but is caused by the tilting of the practically rigid ${\text{MnO}}_5$ block. This tilting occurs just to provide closer packing, and as a result the oxygen ions move closer to the rather small $Y$ ions [Fig. 2(d)].

Type-II multiferroics: Magnetic multiferroics

The biggest excitement nowadays is caused by the discovery of a novel class of multiferroics in which ferroelectricity exists only in a magnetically ordered state and is caused by a particular type of magnetism [10,11]. For example, in ${\text{TbMnO}}_3$ magnetic ordering appears at $T_{\text{N1}}=41\text{K}$, and at a lower temperature, $T_{\text{N2}}=28\text{K}$, the magnetic structure changes. It is only in the low-temperature phase that a nonzero electric polarization appears. Similar behavior occurs in ${\text{TbMn}}_2{\text{O}}_5$.

The first paper to study ${\text{TbMnO}}_3$ showed that a magnetic field can strongly influence the electric polarization: e.g., in ${\text{TbMnO}}_3$ the polarization rotates (or “flops”) by 90 degrees when a critical magnetic field is applied along a certain direction [10]. In ${\text{TbMn}}_2{\text{O}}_5$ [11] the influence of an external field is even stronger: the polarization changes sign with field, and a field alternating between $+1.5$ and $-1.5$ Tesla leads to corresponding oscillations in the polarization. Since the discovery of these materials, a number of other type-II multiferroics with strong magnetoelectric coupling have been discovered and studied.

From the point of view of the mechanism of multiferroic behavior, one can divide type-II multiferroics into two groups: those in which ferroelectricity is caused by a particular type of magnetic spiral and those in which ferroelectricity appears even for collinear magnetic structures.

Spiral type-II multiferroics

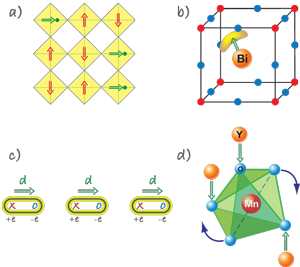
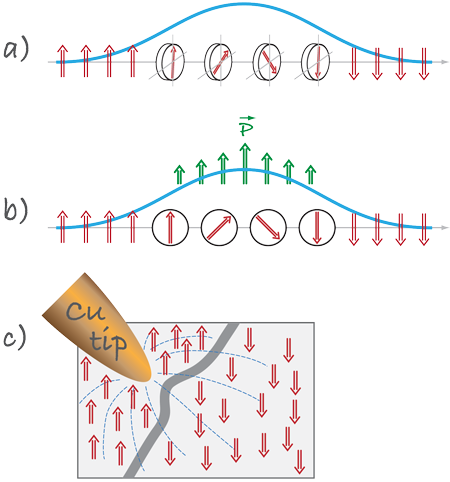
Most of the type-II multiferroics known to date belong to this subgroup. Ferroelectricity appears in conjunction with a spiraling magnetic phase, mostly of the cycloid type. This is the case in ${\text{TbMnO}}_3$, ${\text{Ni}}_3{\text{V}}_2{\text{O}}_6$, and ${\text{MnWO}}_4$. In ${\text{TbMnO}}_3$ below $T_{\text{N1}}=41\text{K}$ the magnetic structure is a sinusoidal spin-density wave, where all spins point in one direction, but the size of the local moment varies periodically in space [Fig. 3(a)]. (Note, this is actually a sort of antiferomagnetic phase because the total moment for the magnet is zero.) Below $T_{\text{N2}}=28\text{K}$, the $\text{Mn}$ spins order so that the tip of the spins sweep out a cycloid [Fig. 3(b)].

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

Katsura, Nagaosa, and Balatsky [25], using a microscopic approach, and Mostovoy [26], using a phenomenological approach, showed that in a cycloidal spiral a polarization, P, appears, that is given by:

$$\mathbf{\text{P}}\sim {\mathbf{\text{r}}}_{ij}\times [{\mathbf{\text{S}}}_i\times {\mathbf{\text{S}}}_j]\sim [\mathbf{\text{Q}}\times \mathbf{\text{e}}]$$

(1)

where ${\mathbf{\text{r}}}_{ij}$ is the vector connecting neighboring spins ${\mathbf{\text{S}}}_i$ and ${\mathbf{\text{S}}}_j$, $\mathbf{\text{Q}}$ is the wave vector describing the spiral, and $\mathbf{\text{e}}\sim [{\mathbf{\text{S}}}_i\times {\mathbf{\text{S}}}_j]$ is the spin rotation axis [Fig. 3(b)]. The microscopic mechanism of this polarization is connected with the spin-orbit interaction (see Refs. [25] and [17], No. 434208).

Magnetic frustration is the source of spiral magnetic ordering in an insulators. Therefore, these type-II multiferroics are usually found in frustrated systems—a good example of how the study of magnetic frustration, itself a hot topic, has lead to new findings with potentially very important applications.

From these ideas and Eq. (1), one can understand the role of a magnetic field. The effect of an external field H on a cycloid is analogous to the well-known spin-flop transition in an antiferromagnet: in a magnetic field, the sublattice moments prefer to lie in a plane perpendicular to the field so they cant in the direction of the field with less cost in exchange energy between neighboring spins. Consequently, when a magnetic field forces the plane of a magnetic cycloid to flop by 90 degrees, the polarization P also flops: according to Eq. (1), P lies in the plane of spins but perpendicular to Q.

One word of caution about Eq. (1): Its derivation assumes a particular crystal symmetry, such as simple cubic or tetragonal. In these cases, Eq. (1) is indeed valid, and, for example, the polarization of a proper screw indicated in Fig. 3(c), in which spins rotate in the plane perpendicular to the wave vector of a spiral Q, would be zero. However, as recently shown by Arima [27], this may not be the case for other symmetries, in which case there may appear a nonzero polarization even for a proper screw spiral. Experimentally, this was observed in $\text{RbFe}({\text{MoO}}_4{)}_3$ [28] and more recently in other layered triangular systems such as ${\text{CuFeO}}_2$ and $A{\text{CrO}}_2$ $(A=\text{Cu, Ag, Li, Na})$ [29].

Type-II multiferroics with collinear magnetic structures

The second group of magnetically driven ferroelectrics are those in which ferroelectricity appears in collinear magnetic structures—that is all magnetic moments aligned along a particular axis—without the necessary involvement of the spin-orbit interaction. Polarization can appear in these materials as a consequence of exchange striction because the magnetic coupling varies with the atomic positions. The simplest example, found in ${\text{Ca}}_3{\text{CoMnO}}_6$ [21], coincides with that shown in Fig. 2(c). ${\text{Ca}}_3{\text{CoMnO}}_6$ consists of one-dimensional chains of alternating ${\text{Co}}^{2+}$ and ${\text{Mn}}^{4+}$ ions. At high temperature the distances between the ions along the chain are the same, the chain has inversion symmetry, and polarization is absent. Magnetic ordering, however, breaks inversion symmetry: the spins form a $\uparrow \uparrow \downarrow \downarrow$ type magnetic structure. Due to an exchange striction the distortion of ferro and antiferro bonds ( $\uparrow \uparrow$ and $\uparrow \downarrow$) is different, and we end up in the situation of Fig. 2(c): the material becomes ferroelectric. Theoretical calculations [30] confirm this picture.

In the case of ${\text{Ca}}_3{\text{CoMnO}}_6$, exchange striction arises from transition metal ions with a different valence ( ${\text{Co}}^{2+}$ and ${\text{Mn}}^{4+}$). One can, however, get the same effect even for identical magnetic ions, when one takes into account that the exchange in transition metal oxides usually occurs via intermediate oxygens and depends on both the distance between the metal ions and the metal-oxygen-metal bond angle. In $R{\text{MnO}}_3$ perovskites where $R$ is a small rare earth, the $\text{Mn}$ magnetic order in the basal plane is of the type $\uparrow \uparrow \downarrow \downarrow$. As proposed by Sergienko, Sen, and Dagotto [31], exchange striction in this case can cause the oxygen ions to shift perpendicular to the $\text{Mn-Mn}$ bonds, which produces a polarization along the direction of the shift. This effect was observed in [32], although its value was much less than estimated theoretically [31,33].

One more mechanism giving ferroelectricity even in a collinear magnet is the “electronic” ferroelectricity in frustrated magnets [34]: the polarization of a triangle of spins is proportional to the spin correlation function ${\mathbf{\text{S}}}_1({\mathbf{\text{S}}}_2+{\mathbf{\text{S}}}_3)-2{\mathbf{\text{S}}}_2{\mathbf{\text{S}}}_3$ (the numbers denote positions on vertices of the triangle), and is nonzero if the latter is nonzero.

The lessons we learned by studying multiferroics, especially those of type-II, are very helpful to predict or explain a number of miscellaneous phenomena, some of which can be very useful for potential applications. Consider for example the usual domain wall in a ferromagnet. There are two types of such walls, schematically shown in Fig. 4. The wall shown in Fig. 4(a) is called a Bloch domain wall; in it the magnetization at the wall rotates in the plane of the wall, perpendicular to the direction Q from one domain to the other. In the other case, Fig. 4(b), which is called a Néel domain wall, spins rotate in the plane containing Q. Comparing Fig. 4 and Fig. 3, one immediately sees that one can consider the Néel domain wall as a part of a cycloidal spiral. According to the expressions in Eq. (1) we then should expect that in such a domain wall the electric polarization will form, localized in the wall and directed as shown in Fig. 4.

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

If now we put a system with such a Néel domain wall in the gradient of an electric field, the wall and the electric dipole associated with it will be either pulled toward the region of stronger field or pushed out of it, depending on the orientation of a dipole. This effect was recently suggested by Dzyaloshinskii [35], but even before his prediction it was actually discovered and studied experimentally by a group in Moscow [36]. They did a conceptually very simple experiment: using films of the well-known insulating ferromagnet with a high transition temperature, iron garnet ${\text{(BiLu)}}_3{\text{(FeGa)}}_5{\text{O}}_{12}$, they brought a sharpened copper wire to the surface and applied a voltage pulse. Under the influence of the resulting inhomogeneous electric field, the domain walls in the film, which they visualized magneto-optically, start to move (or rather bend). They concluded that this happens because of the mechanism described above, and the authors could even estimate the resulting velocity of a domain wall. This observation, besides confirming our general understanding, may be potentially very important, as it could prove to be a means of controlling domain structure, and consequently magnetic memory, by applying a voltage rather than magnetic field or electric current.

Similarly, local electric polarization should appear in magnetic vortices, which are also widely studied nowadays as a possible route to nonvolatile magnetic memory [37]. To the best of my knowledge nobody yet tried to influence such vortices in magnetic insulators by an electric field (without currents).

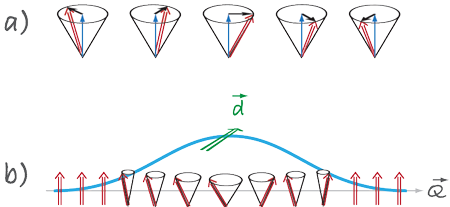
One more effect can be proposed. Consider an insulating ferromagnet that contains a spin wave (a magnon). The real microscopic picture of a spin wave is the one shown in Fig. 5(a): the magnon is a spin deviation from the average magnetization M, with each spin precessing around M in time and with the phase shifts along the propagation direction. But from Fig. 5(a) we see that the instantaneous picture (the snapshot) of a spin wave is a cone with constant M and with the perpendicular component forming a cycloid. According to Eq. (1), there should appear in such a spin wave an electric polarization perpendicular to the magnetization and to the propagation vector. Actually such a polarization was discovered for a static conic magnetic structure in ${\text{CoCr}}_2{\text{O}}_4$ (Ref. [17], No. 434204). Here, if we create a spin wave in the form of a wave packet, this wave packet will carry with it both magnetization $\mathrm{\Delta }\mathbf{\text{M}}$ and an electric dipole moment d that moves with it [Fig. 5(b)].

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

Another spin-off from the physics discussed above concerns the magnetic structure of magnetic films on different substrates. A beautiful experiment, carried out recently in Germany [38], demonstrated that in an atomically thin layer of manganese on tungsten, the $\text{Mn}$ does not form a simple antiferromagnetic structure, as one would expect, but a long-periodic cycloidal spiral. And, most surprisingly, all such spirals have the same sense of spin rotation. Even earlier the observation was made by the same group that the Néel domain walls in the atomically thin layers of iron on tungsten also have a unique sense of spin rotation [39].

At first glance this is a very unexpected phenomenon. However, it becomes immediately clear if we remember the physics described by Eq. (1). According to this relation, a cycloidal magnetization in a type-II multiferroic creates a polarization, but we should also expect an inverse effect: a nonzero polarization would create a cycloidal spiral. This is apparently what happens in thin films of manganese and iron on tungsten studied in [38,39] (and it is also the origin of a magnetic spiral in ${\text{BiFeO}}_3$ ). Close to the surface there exists a drop of the potential (i.e., the work function), and a dipole layer forms at the surface, which produces an electric field perpendicular to the surface. This field creates a local polarization P normal to the surface that turns a collinear magnetic structure into a cycloidal spiral.

Microscopically the mechanism for this effect is antisymmetric, or Dzyaloshinskii-Moriya, exchange of the type $\mathbf{\text{D}}\cdot [{\mathbf{\text{S}}}_1\times {\mathbf{\text{S}}}_2]$. This was indeed proposed in the original publications [38,40] as an explanation of the observed effect. The use of the knowledge acquired in the study of multiferroics makes this effect very simple and transparent. One has an impression that it should be present and should be taken into account in all magnetic thin films, although the strength of it would of course depend on the particular situation.

The field of multiferroics, becides promising important applications, contains rich and interesting physics. It is now a very active and fruitful field. A lot is already known, many basic principles are established. Thus, what is next?

One can think of several promising directions, some of which have already been pursued. First, the search for new multiferroics is still proceeding at a rapid pace, and one should expect that many new examples and even new classes will be discovered. Each new multiferroic is a challenge in itself, every substance has its own material-specific aspects, which one has to explore.

Then, the understanding of the basic physics, together with the progress of ab initio calculations, opens a way to create “multiferroics by design.” Examples of this approach can be found in [41].

From the point of view of the basic physics, we should mention the idea of toroidal moments—the third set of moments of electromagnetic field, besides the well-known electric and magnetic moments. Three basic ferroic properties—ferroelasticity (characterized by the strain ${\epsilon }_{ij}$), ferroelectricity (polarization P) and (ferro)magnetism (magnetic moments M) have different transformation properties with respect to spatial inversion $I$ and time reversal $T$: strain is $I$ and $T$ even, P is $I$ odd and $T$ even, M is $I$ even and $T$ odd. There exists yet the fourth possibility: a quantity which is both $I-$ and $T-$odd. It can of course be simply a coexistence of polarization and magnetism, which we have in all multiferroics. But there exists also a special quantity with such symmetry, which is called a toroidal moment (or sometimes anapole moment). The details one can find in Ref. [17], No. 434203; in the simplest case it can be defined as

The relation between toroidal moments and multiferroicity is not straightforward. Both are $I-$ and $T-$odd, but it does not mean that all multiferroics have $⟨\mathbf{\text{T}}⟩\ne 0$ or, vice versa, all systems with nonzero toroidal moments are multiferroics. What one can show is that toroidal moments are directly related to the antisymmetric magnetoelectric effect. As toroidal moments have now been observed in several systems, we can expect to see more emerge from these ideas [42,43].

One more big direction in the study of multiferroics, which I did not touch upon above, is the investigation of their dynamical properties and elementary excitations. From the intricate coupling between spin and charge degrees of freedom in multiferroics, one can expect quite nontrivial features of such excitations, such as the possibility to excite magnons with an electric field. And indeed, these effects were already discovered experimentally, giving rise to the term “electromagnon” (see Refs. [44] and [17], No. 434210). In general, the investigation of dynamical effects in multiferroics will certainly be expanded in future.

And of course I left out the very big, and from a practical point of view probably the most promising direction: the fabrication and study of “artificial” composite multiferroics. For example, magnetic and ferroelectric materials can be combined in the form of multilayers or self-organized nanostructures. The coupling between magnetic and ferroelectric subsystems in this case usually occurs via strain (although in principle it is not the only coupling channel), i.e., one tries to use magnetic systems with strong magnetostriction and ferroelectrics with large piezoelectric coefficients. The study of these objects is now an extremely active field and has already produced some spectacular achievements (such as the creation of tiny magnetic sensors with the sensitivity exceeding that of even superconducting quantum interference devices (SQUIDs) [45] Some of the results in this field are presented in reviews [14,16,46] and Ref. [17], No. 434220.

Summarizing, I can say that the field of multiferroics and magnetoelectrics as a part of a recent trend to create and use multifunctional materials, is already an extremely active field. And one can be sure that there is still much more to come, and the development of this field will go still very actively both in the direction of basic physics and in applications, where, it seems, these materials have a bright future.

Corrections (10 March 2009): Paragraph 10, sentence 6, “called type-I” changed to “which can be called type-I”. Paragraph 31, sentence 6, “rather than electric current” changed to “rather than magnetic field or electric current.”