Giving light yet another new twist

Martin Wegener; Stefan Linden

Viewpoint

Giving light yet another new twist

Institut für Angewandte Physik, Universität Karlsruhe (TH) and Institut für Nanotechnologie, Forschungszentrum Karlsruhe GmbH, Karlsruhe, Germany

January 12, 2009• Physics 2, 3

Metamaterials can be designed to rotate light as it passes through them. If the effect is strong enough, it can lead to the material having a negative index of refraction and light bouncing around very differently than expected.

Figure caption — **Figure 1:** Different paths toward a chiral metamaterial, which can rotate the polarization of incident light. (a) A planar array of metallic split-ring resonators is chiral when light strikes the surface of the plane at an oblique angle. (b) An elongated split-ring resonator is chiral even at normal-incidence. (c) The bilayered metallic chiral structure has a negative index of refraction at microwave frequencies [1].

To completely control the flow of an electromagnetic wave inside of matter, one needs the ability to manipulate both the electric and magnetic components of light with microscopic electric and magnetic dipoles, respectively. While the atoms in natural solids generally do not provide this level of control, artificial atoms in metamaterials can. In a paper in Physical Review B, Eric Plum and coworkers at the University of Southampton in the UK and collaborators in the US, China, and Greece have fabricated such a structure, in which both the electric and magnetic components of light excite strong electric and magnetic dipoles [1]. At microwave frequencies this structure has an effective negative index of refraction. This means that the phase velocity of the wave is opposite to the electromagnetic energy flow. In a separate paper appearing in Physical Review Letters [2], Shuang Zhang and colleagues at the University of California at Berkeley and Oklahoma State University, both in the US, describe a closely related structure that can operate at $THz$ frequencies. If these structures could be further engineered to work in optical and visible frequency ranges, strong optical activity might enable novel types of optical devices.

In circularly polarized light, the tip of the electric field sweeps out a spiral in real space. The pitch of this spiral is simply the wavelength of light, while the handedness (or chirality) depends on whether the spiral sweeps clockwise or counterclockwise as the light wave moves along its path. It is intuitively clear that the interaction of circularly polarized light with matter that also has a spiral structure—a chiral molecule or an artificial nanostructure—will depend on the relative handedness between the two. This is the basis of the well-known optical activity in milk or sugar solutions, both of which contain chiral molecules that cause the polarization of an incident, linearly polarized wave to gradually rotate as it passes through the medium. It is perhaps less well known that the microscopic origin of this effect is magnetic dipoles that are excited by the electric component of the light and vice versa [3–7]. In a plane wave, the incident electric and magnetic vector components are perpendicular to each other. If, as the wave passes through a medium, the magnetic component induces an electric dipole parallel to the magnetic field vector, the resulting net local electric field vector will be rotated a bit. It can be shown that reciprocity demands that, likewise, magnetic dipoles are excited by the electric vector component. Hence the magnetic field vector rotates as well.

Mathematically, the relations between the relevant components of the electromagnetic fields in the macroscopic Maxwell equations become $D = ϵ_{0} ϵ E + i κ / c_{0} H$ and $B = - i κ / c_{0} E + μ_{0} μ H$ [3,5]. Here, $κ$ is the dimensionless chirality parameter and the other symbols have their usual meaning. The refractive index, $n$ , for right- (+) and left-handed (-) circular polarization becomes $n_{\pm} = (ϵ μ)^{1 / 2} \pm κ$ . For a sugar solution, however, the magnitude of the induced magnetic dipoles is extremely small and both refractive indices, $n_{\pm}$ , are positive, while the difference between them, $(n_{+} - n_{-}) = 2 κ$ , is tiny. To observe a significant polarization rotation effect in sugar water, the light would have to pass through more than several centimeters (tens of thousands of visible wavelengths) of liquid.

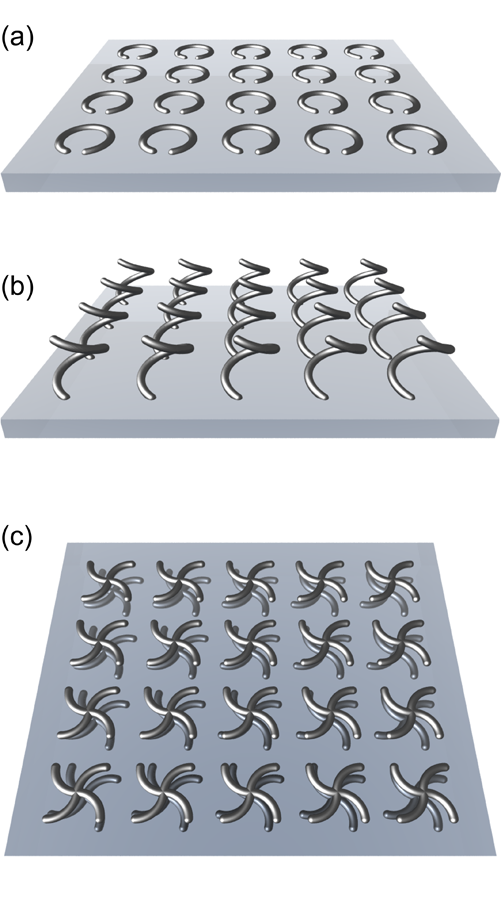
Metamaterials [8,9] can boost this effect by several orders of magnitude. In place of molecules, one can engineer tiny, subwavelength resonant electromagnets that act as magnetic dipoles [10,11]. Figure 1(a) shows an array of split-ring resonators that could make up a metamaterial: by Faraday’s law, a time-varying magnetic field perpendicular to the plane of these rings induces an oscillating electric current in the rings, so that each acts as a miniature magnetic dipole [10]. Alternatively, an electric current, and hence a magnetic moment, can also be induced by applying a voltage drop between the two ends of the split ring. If light comes in perpendicular to a plane of these resonators, the induced magnetic dipoles will point along the propagation direction of the light. Hence, in this geometry, the structure is not chiral. In contrast, for an oblique incidence of light [12], the plane of split-ring resonators does have a chirality [13]. The same effect can work for normal-incidence light by stretching each split-ring resonator out of the substrate plane so that it forms one winding of a three-dimensional spiral [see Fig. 1(b)].

For such three-dimensional chiral metamaterials, the effect of optical activity can be so strong that the refractive index becomes negative for one circular polarization—in principle, even if the electric permittivity $ϵ$ and magnetic permeability $μ$ are both positive. The design challenge lies in optimizing the structure parameters in a way that is compatible with fabrication restrictions. Plum et al. [1] have made a structure like the one schematically shown in Fig. 1(c). Here, chirality is achieved by layering arrays of metal pinwheels so that the pinwheels in one layer are rotated by 15 degrees from those in the next layer. Notably, the authors observe polarization rotation angles as large as about $\pm 45$ degrees for only two such layers of the metal pinwheels, which is both less than one wavelength of a microwave in free-space and a single lattice constant (that is, for a complete winding) of the metamaterial. In the distinct but related structure by Zhang et al. [2], the chiral unit cell is essentially composed of a set of four split-ring resonators normal to the substrate plane and not parallel to each other.

Zhang et al. reach the $THz$ frequency range by employing standard microlithography techniques, while Plum et al. are able to reach $GHz$ frequencies by using circuit-board printing technology at microwave frequencies. Both frequency regimes have important applications. For example, the $GHz$ range is important for mobile-phone antenna technology, while gas-phase molecule sensing or security detection can operate at $THz$ .

The two papers [1,2] go significantly beyond previous experimental work on chiral metamaterials [14–19] in that the authors convincingly demonstrate that one of the refractive indices is indeed negative. They do this by analyzing transmission and reflectance of light at normal incidence to the chiral structure and keeping track of the light’s phase. The work [1,2] is further distinct from previous metamaterials in which the negative index of refraction comes solely from negative permittivity and negative permeability [20,21]. The improved design flexibility for metamaterials brought about by the chirality parameter $κ$ raises further hopes that future metamaterials may become more than just an interesting scientific obscurity. However, tremendous challenges are still ahead. To reach optical frequencies, the elements in the metamaterial have to be miniaturized to the nanometer scale, losses need to be reduced significantly and structures need to become truly three dimensional.

Furthermore, structures that are isotropic rather than the uniaxial structures designed by Plum et al. and Zhang et al. may be desirable for certain applications. For example, one mind-boggling effect that has been predicted theoretically for isotropic and strongly chiral structures is “negative reflection,” which can be used for focusing of light [22]. At the interface between the chiral medium and a perfect metallic conductor, for one circular polarization, the incident wave direction and that of the reflected wave lie on the same side of the normal to the interface—in sharp contrast to usual reflection of light by a mirror. Further surprises in optics can surely be expected from the new “twist” that strongly chiral structures bring to light.

References

E. Plum, J. Zhou, J. Dong, V. A. Fedotov, T. Koschny, C. M. Soukoulis, and N. I. Zheludev, Phys. Rev. B 79, 035407 (2009)
S. Zhang, Y-S. Park, J. Li, X. Lu, W. Zhang, and X. Zhang, Phys. Rev. Lett. 102, 023901 (2009)
S. Tretyakov, I. Nefedov, A. Sihvola, S. Maslovski, and C. Simovski, J. Electromagn. Waves Appl. 17, 695 (2003)
J. B. Pendry, Science 306, 1353 (2004)
S. Tretyakov, A. Sihvola, and L. Jylhä, Photonics Nanostruct. Fundam. Appl. 3, 107 (2005)
V. M. Agranovich and Y. N. Gartstein, Physics-Uspekhi 49, 1029 (2006)
J. Kästel, M. Fleischhauer, S. F. Yelin, and R. L. Walsworth, Phys. Rev. Lett. 99, 073602 (2007)
Electromagnetic Metamaterials: Physics and Engineering Explorations, edited by N. Engheta and R. Ziolkowski (John Wiley and Sons, 2006) [Amazon][WorldCat]
K. Busch, G. von Freymann, S. Linden, S. F. Mingaleev, L. Tkeshelashvili, and M. Wegener, Phys. Rep. 444, 101 (2007)
J. B. Pendry, A. J. Holden, D. J. Robbins, and W. J. Stewart, IEEE Trans. Microwave Theory Tech. 47, 2075 (1999)
S. Linden, C. Enkrich, M. Wegener, J. Zhou, T. Koschny, and C. M. Soukoulis, Science 306, 1351 (2004)
J. Zhou, T. Koschny, and C. M. Soukoulis, Phys. Rev. Lett. 95, 203901 (2005)
E. Plum, V. A. Fedotov, and N. I. Zheludev, Appl. Phys. Lett. 93, 191911 (2008)
Y. Svirko, N. I. Zheludev, and M. Osipov, Appl. Phys. Lett. 78, 498 (2001)
A. S. Schwanecke, A. Krasavin, D. M. Bagnall, A. Potts, A. V. Zayats, and N. I. Zheludev, Phys. Rev. Lett. 91, 247404 (2003)
J. Turunen and Y. Svirko, Phys. Rev. Lett. 95, 227401 (2005)
A. V. Rogacheva, V. A. Fedotov, A. S. Schwanecke, and N. I. Zheludev, Phys. Rev. Lett. 97, 177401 (2006)
F. Miyamarua and M. Hangyob, Appl. Phys. Lett. 89, 211105 (2006)
M. Decker, M. W. Klein, M. Wegener, and S. Linden, Opt. Lett. 32, 856 (2007)
V. M. Shalaev, Nature Photon. 1, 41 (2007)
C. M. Soukoulis, S. Linden, and M. Wegener, Science 315, 47 (2007)
C. Zhang and T. J. Cui, Appl. Phys. Lett. 91, 194101 (2007)

About the Authors

Martin Wegener has a joint appointment as professor of physics at Universität Karlsruhe (TH) and Forschungszentrum Karlsruhe GmbH. He is also coordinator of the DFG-Center for Functional Nanostructures (CFN) at Universität Karlsruhe (TH). His current research interests comprise photonic metamaterials, photonic crystals, and nanophotonics.

Stefan Linden received his Ph.D. in Physics at Universität Marburg in 2002. Thereafter, he was a postdoc at the University of Toronto in 2002–2003 and at Universität Karlsruhe (TH) in 2003–2005. Since 2006 he has been heading an Independent Junior Research Group on “Metamaterials for Photonics” at Institut für Nanotechnologie at Forschungszentrum Karlsruhe GmbH.