Is a room-temperature, solid-state quantum computer mere fantasy?

What is a computer? Standard classical computers use bits for encoding numbers, and the bits are manipulated by the classical gates that can execute AND and OR operations, for example. A classical bit has a value of 0 or 1, according to whether some small subunit is electrically charged or uncharged. Other forms are possible: the bits for a classical spintronic computer might be spins along or opposite to a magnetic field. Even the most modest computers on sale today incorporate complex networks of a few types of gates to control huge numbers of bits. If there are so few bits that you can count them on your fingers, it can’t seriously be considered a computer.

What do we mean by quantum? Being sure a phenomenon is “quantum” isn’t simple. Quantum ideas aren’t intuitive yet. Could you convince your banker that quantum physics could improve her bank’s security? Perhaps three questions identify the issues. First, how do you describe the state of a system? The usual descriptors, wave functions and density matrices, underlie wavelike interference and entanglement. Entanglement describes the correlations between local measurements on two particles, which I call their “quantum dance.” Entanglement is the resource that could make quantum computing worthwhile. The enemy of entanglement is decoherence, just as friction is the enemy of mechanical computers. Second, how does this quantum state change if it is not observed? It evolves deterministically, described by the Schrödinger equation. The probabilistic results of measurements emerge when one asks the third question: how to describe observations and their effects. Measurement modifies entanglement, often destroying it, as it singles out a specific state. This is one way that you can tell if an eavesdropper intercepted your message in a quantum communications system.

Proposed quantum computers have qubits manipulated by a few types of quantum gates, in a complex network. But the parallels are not complete [2]. Each classical bit has a definite value, it can only be 0 or 1, it can be copied without changing its value, it can be read without changing its value and, when left alone, its value will not change significantly. Reading one classical bit does not affect other (unread) bits. You must run the computer to compute the result of a computation. Every one of those statements is false for qubits, even that last statement. There is a further difference. For a classical computer, the process is Load $\to$ Run $\to$ Read, whereas for a quantum computer, the steps are Prepare $\to$ Evolve $\to$ Measure, or, as in one case discussed later, merely Prepare $\to$ Measure.

Why do we need a quantum computer? The major reasons stem from challenges to mainstream silicon technology. Markets demand enhanced power efficiency, miniaturization, and speed. These enhancements have their limits. Future technology scenarios developed for the semiconductor industry’s own roadmap [3] imply that the number of electrons needed to switch a transistor should fall to just 1 (one single electron) before 2020. Should we follow this innovative yet incremental roadmap, and trust to new tricks, or should we seek a radical technology, with wholly novel quantum components operating alongside existing silicon and photonic technologies? Any device with nanoscale features inevitably displays some types of quantum behavior, so why not make a virtue of necessity and exploit quantum ideas? Quantum-based ideas may offer a major opportunity, just as the atom gave the chemical industry in the 19th century, and the electron gave microelectronics in the 20th century. Quantum sciences could transform 21st century technologies.

Why choose the solid state for quantum computing? Quantum devices nearly always mean nanoscale devices, ultimately because useful electronic wave functions are fairly compact [4]. Complex devices with controlled features at this scale need the incredible know-how we have acquired with silicon technology. Moreover, quantum computers will be operated by familiar silicon technology. Operation will be easier if classical controls can be integrated with the quantum device, and easiest if the quantum device is silicon compatible. And scaling up, the linking of many basic and extremely small units is a routine demand for silicon devices. With silicon technologies, there are also good ways to link electronics and photonics. So an ideal quantum device would not just meet quantum performance criteria, but would be based on silicon; it would use off-the-shelf techniques (even sophisticated ones) suitable for a near-future generation fabrication plant. A cloud on the horizon concerns decoherence: can entanglement be sustained long enough in a large enough system for a useful quantum calculation?

It has been done already? Some beautiful work demonstrating critical steps, including initializing a spin system and transfer of quantum information, has been done at room temperature with nitrogen-vacancy ( ${\text{NV}}^{-}$) centers in diamond [5]. Very few qubits were involved, and scaling up to a useful computer seems unlikely without new ideas. But the combination of photons—intrinsically insensitive to temperature—with defects or dopants with long decoherence times leaves hope.

It can’t be done: serious quantum computing simply isn’t possible anyway. Could any quantum computer work at all? Is it credible that we can build a system big enough to be useful, yet one that isn’t defeated by loss of entanglement or degraded quantum coherence? Certainly there are doubters, who note how friction defeated 19th century mechanical computers. Others have given believable arguments that computing based on entanglement is possible [6]. Of course, it may prove that some hybrid, a sort of quantum-assisted classical computing, will prove the crucial step.

It can’t be done: quantum behavior disappears at higher temperatures. Confusion can arise because quantum phenomena show up in two ways. In quantum statistics, the quantal $\mathrm{ħ}$ appears as $\mathrm{ħ}\omega /kT$. When statistics matter most, near equilibrium, high temperatures $T$ oppose the quantum effects of $\mathrm{ħ}$. However, in quantum dynamics, $\mathrm{ħ}$ can appear unassociated with $T$, opening new channels of behavior. Quantum information processing relies on staying away from equilibrium, so the rates of many individual processes compete in complex ways: dynamics dominate. Whatever the practical problems, there is no intrinsic problem with quantum computing at high temperatures.

It can’t be done: the right qubits don’t exist. True, some qubits are not available at room temperature. These include superconducting qubits and those based on Bose-Einstein condensates. In Kane’s seminal approach [7], the high polarizability needed for phosphorus-doped silicon ( $\text{Si:P}$) corresponds to a low ionization donor energy, so the qubits disappear (or decohere) at room temperature. In what follows, I shall look at methods without such problems.

David DiVincenzo at IBM Research Labs devised a checklist [8] that conveniently defines minimal (but seriously challenging) needs for a credible quantum computer. There must be a well-defined set of quantum states, such as electron spin states, to use as qubits. One needs scalability, so that enough qubits (let’s say 20, though 200 would be better) linked by entanglement are available to make a serious quantum computer. Operation demands a means to initialize and prepare suitable pure quantum states, a means to manipulate qubits to carry out a desired quantum evolution, and means to read out the results. Decoherence must be slow enough to allow these operations.

What does this checklist imply for solid-state quantum computing? Are there solid-state systems with decoherence mechanisms, key energies, and qubit control systems that might work at useful temperatures, ideally room temperature? Solid-state technologies have good prospects for scalability. There is a good chance that there are ingenious ways to link the many qubits and quantum gates needed for almost any serious application. However, decoherence might be fast. This may be less of a problem than imagined, for fast operating speeds go hand in hand with fast decoherence. Fast processing needs strong interactions, and such strong interactions will usually cause decoherence [9].

For spin-based solid-state quantum computing, most routes to initialization group into four categories. First, there are optical methods (including microwaves), based on selection rules, such as those used for ${\text{NV}}^{-}$ experiments. Then there are spintronic approaches, using a source (perhaps a ferromagnet) of spin-polarized electrons or excitons. (Note that spins have been transferred over distances of nearly a micron at room temperature [10].) Then there are brute force methods aiming for thermal equilibrium in a very large magnetic field, where the ratio of Zeeman splitting to thermal energy $k_{B}T$ is large. And finally there are tricks involving extra qubits that are not used in calculations. Of these methods, the optical and spintronic concepts seem most promising for room-temperature operation.

For readout, there are two broad strategies. Most ideas for spin-based quantum information processing aim at the sequential readout of individual spins. However, there are other less-developed ideas in which the ensemble of relevant spins is looked at together, as in some neutron scattering studies of antiferromagnetic crystals. What methods are there for probing single spins, if the sequential strategy is chosen? First, there is direct frequency discrimination, including the use of Zeeman splitting, of hyperfine structure, and so on. Ideas from atom trap experiments suggest that one can continue to interrogate a spin with a sequence of photons that do not change the qubit [11]. Such methods might work at room temperature, at least if the relevant spectral lines remain sharp enough. Second, there are many ways to exploit spin-dependent rates of carrier scatter or trapping. One might examine how mobile polarized spins are scattered by a fixed spin that is to be measured. Or the spin of a mobile carrier might be measured by its propensity for capture or scatter by fixed spin, or by some combination of polarized mobile spins and interferometry. At room temperature, the problem is practice rather than principle, and acceptable methods seem possible. A third way is to use relative tunnel rates, where one spin state can be blocked. Tunneling-based methods can become very hard at higher temperatures. There are then various ideas, all of which seem to be both tricky and relatively slow, but I may be being pessimistic. These include the use of circularly polarized light and magneto-optics, the direct detection of spin resonance with a scanning tunneling microscope, the exploitation of large spin-orbit coupling, or the direct measurement of a force with a scanning probe having a magnetic tip.

For the manipulations during operation, probably the most important ways use electromagnetic radiation, whether optical, microwave or radio frequency. Other controls, such as ultrasonics or surface acoustic waves, are less flexible. Electromagnetic methods might well operate at room temperature. Other suggestions invoke nanoscale electrodes. I do not know of any that look both credible and scalable.

In what follows, I shall concentrate on two proposals as examples, with apologies to those whose suggestions I am omitting. Both of the proposals use optical methods to control spins, but do so in wholly different ways. The first is a scheme for optically controlled spintronics that I, Andrew Fisher, and Thornton Greenland proposed [11,12]. The second route exploits entanglement of states of distant atoms by interference [13] in the context of measurement-based quantum computing [14]. A broader discussion of the materials needed is given in Ref. [15].

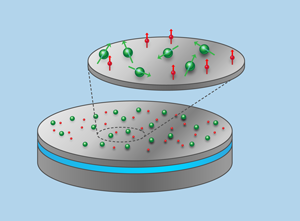
Optically controlled spintronics [11,12]. Think of a thin film of silicon, perhaps $10\text{nm}$ thick, isotopically pure to avoid nuclear spins, on top of an oxide substrate (Fig. 1). The simple architecture described is essentially two dimensional. Now imagine the film randomly doped with two species of deep donor—one species as qubits, the other to control the qubits. In their ground states, these species should have negligible interactions. When a control donor is excited, the electron’s wave function spreads out more, and its overlap with two of the qubit donors will create an entangling interaction between those two qubits (Fig. 2). Shaped pulses of optical excitation of chosen control donors guide the quantum dance (entanglement) of chosen qubit donors [16].

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

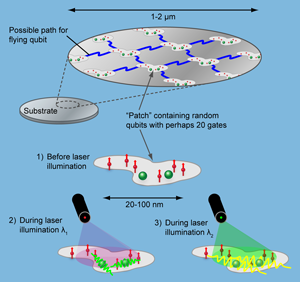
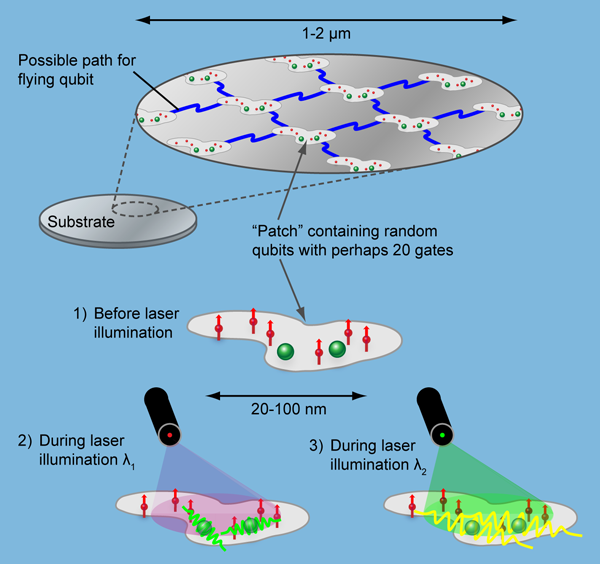
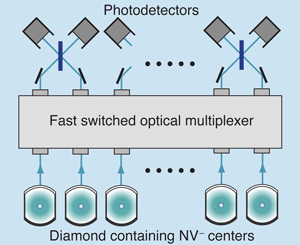
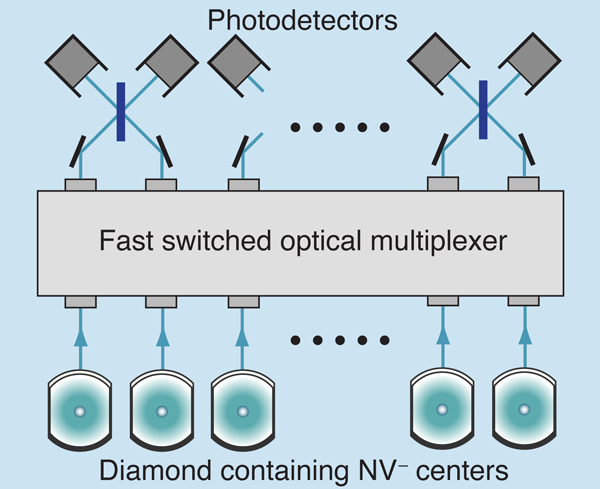
For controlling entanglement in this way, typical donor spacings in silicon must be of the order of tens of nanometers. Optically, one can only address regions of the order of a wavelength across, say $1000\text{nm}$. The limit of optical spatial resolution is a factor 100 larger than donor spacings needed for entanglement. How can one address chosen pairs of qubits? The smallest area on which we can focus light contains many spins. The answer is to exploit the randomness inevitable in standard fabrication and doping. Within a given patch of the film a wavelength across, the optical absorptions will be inhomogeneously broadened from dopant randomness. Even the steps at the silicon interfaces are helpful because the film thickness variations shift transition energies from one dopant site to another. Light of different wavelengths will excite different control donors in this patch, and so manipulate the entanglements of different qubits. Reasonable assumptions suggest one might make use of perhaps 20 gates or so per patch. Controlled links among 20 qubits would be very good by present standards, though further scale up—the linking of patches—would be needed for a serious computer (Fig. 3). The optically controlled spintronics strategy [11,12] separates the two roles: qubit spins store quantum information, and controls manipulate quantum information. These roles require different figures of merit.

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

To operate at room temperature, qubits must stay in their ground states, and their decoherence—loss of quantum information—must be slow enough. Shallow donors like $\text{Si:P}$ or $\text{Si:Bi}$ thermally ionize too readily for room-temperature operations, though one could demonstrate principles at low temperatures with these materials. Double donors like ${\text{Si:Mg}}^{+}$ or ${\text{Si:Se}}^{+}$ have ionization energies of about half the silicon band gap and might be deep enough. Most defects in diamond are stable at room temperature, including substitutional $\text{N}$ in diamond and the ${\text{NV}}^{-}$ center on which so many experiments have been done.

What about decoherence? First, whatever enables entanglement also causes decoherence. This is why fast switching means fast decoherence, and slow decoherence implies slow switching. Optical control involves manipulation of the qubits by stimulated absorption and emission in controlled optical excitation sequences, so spontaneous emission will cause decoherence. For shallow donors, like $\text{Si:P}$, the excitation energy is less than the maximum silicon phonon energy; even at low temperatures, one-phonon emission causes rapid decoherence. Second, spin-lattice relaxation in qubit ground states destroys quantum information. Large spin-orbit coupling is bad news, so avoiding high atomic number species helps. Spin lattice relaxation data at room temperature are not yet available for those Si donors (like ${\text{Si:Se}}^{+}$) where one-phonon processes are eliminated because their first excited state lies more than the maximum phonon energy above the ground state. In diamond at room temperature, the spin-lattice relaxation time for substitutional nitrogen is very good ( $\sim 1\text{ms}$) and a number of other centers have times $\sim 0.1\text{ms}$. Third, excited state processes can be problems, and two-photon ionization puts constraints on wavelengths and optical intensities. Fourth, the qubits could lose quantum information to the control atoms. This can be sorted out by choosing the right form of excitation pulses [16]. Fifth, interactions with other spins, including nuclear spins, set limits, but there are helpful strategies, like using isotopically pure silicon [17].

The control dopants require different criteria. The wave functions of electronically excited controls overlap and interact with two or more qubits to manipulate entanglements between these qubits. The transiently excited state wave function of the control must have the right spatial extent and lifetime. While centers like $\text{Si:As}$ could be used to show the ideas, for room-temperature operation one would choose perhaps a double donor in silicon, or substitutional phosphorus in diamond. The control dopant must have sharp optical absorption lines, since what determines the number of independent gates available in a patch is the ratio of the spread of excitation energies, inhomogeneously broadened, to the (homogeneous) linewidth. The spread of excitation energies—inhomogeneous broadening is beneficial in this optical spintronics approach [11,12]—has several causes, some controllable. Randomness of relative control-qubit positions and orientations is important, and it seems possible to improve the distribution by using self-organization to eliminate unusable close encounters. Steps on the silicon interfaces are also helpful, provided there are no unpaired spins. Overall, various experimental data and theoretical analyses indicate likely inhomogeneous widths are a few percent of the excitation energy.

A checklist of interesting systems as qubits or controls shows some significant gaps in knowledge of defects in solids. Surprisingly little is known about electronic excited states in diamond or silicon, apart from energies and (sometimes) symmetries. Little is known about spin lattice relaxation and excited state kinetics at temperatures above liquid nitrogen, except for the shallow donors that are unlikely to be good choices for a serious quantum computer. There are few studies of stabilities of several species present at one time. Can we be sure to have isolated $\text{P}$ in diamond? Would it lose an electron to substitutional $\text{N}$ to yield the useless species ${\text{P}}^{+}$ and ${\text{N}}^{-}$ ? Will most $\text{P}$ be found as the irrelevant (spin $\text{S}=0$) ${\text{PV}}^{-}$ center?

What limits the number of gates in a patch is the number of control atoms that can be resolved spectroscopically one from another. As the temperature rises, the lines get broader, so this number falls and scaling becomes harder. Note the zero phonon linewidth need not be simply related to the fraction of the intensity in the sidebands. Above liquid nitrogen temperatures, these homogeneous optical widths increase fast. Thus we have two clear limits to room-temperature operation. The first is qubit decoherence, especially from spin lattice relaxation. The second is control linewidths becoming too large, reducing scalability, which may prove a more powerful limit.

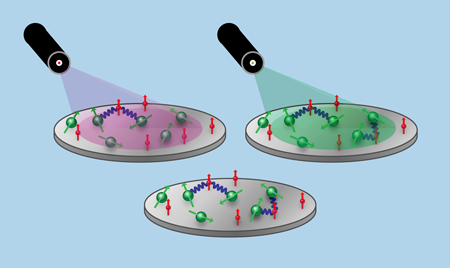
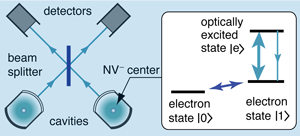
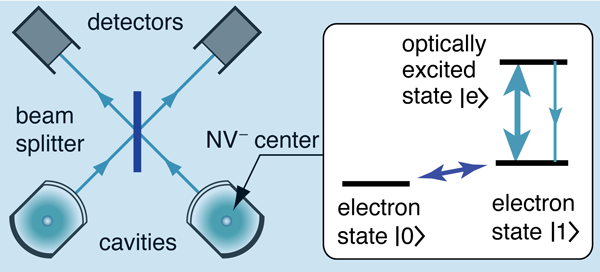
Entangled states of distant atoms or solid-state defects created by interference. A wholly different approach generates quantum entanglement between remote systems by performing measurements on them in a certain way [13]. The systems might be two diamonds, each containing a single ${\text{NV}}^{-}$ center prepared in specific electron spin states, the two centers tuned to have exactly the same optical energies (Fig. 4). The measurement involves “single shot” optical excitation. Both systems are exposed to a weak laser pulse that, on average, will achieve one excitation. The single system excited will emit a photon that, after passing though beam splitters and an interferometer, is detected without giving information as to which system was excited (Fig. 5). “Remote entanglement” is achieved, subject to some strong conditions. The electronic quantum information can be swapped to more robust nuclear states (a so-called brokering process). This brokered information can then be recovered when needed to implement a strategy of measurement-based quantum information processing [14].

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

The materials and equipment needs, while different from those of optically controlled spintronics, have features in common. For remote entanglement, a random distribution of centers is used, with one from each zone chosen because of their match to each other. The excitation energies of the two distant centers must stay equal very accurately, and this equality must be stable over time, but can be monitored. There are some challenges here, since there will be energy shifts when other defect species in any one of the systems change charge or spin state (the difficulty is present but less severe for the optical control approach). As for optically controlled spintronics [11,12], scale-up requires narrow lines, and becomes harder at higher temperatures, though there are ways to reduce the problem. Remote entanglement needs interferometric stability, avoiding problems when there are different temperature fluctuations for the paths from the separate systems. Again, there are credible strategies to reduce the effects.

Spectroscopy is a generic need for both optically controlled spintronics and remote entanglement approaches. Both need qubits (the electron qubit for the measurement-based approach) with slow decoherence, a significant multiple of switching times. Both need sharp optical transitions with weak phonon sidebands to avoid loss of quantum information. A few zero phonon lines do indeed remain sharp at room temperature. The sharp lines should have frequencies stable over extended times. This mix of properties is hard to meet, but by no means impossible.

Perhaps the hardest conditions have yet to be mentioned. A quantum gate is no more a quantum computer than a transistor is a classical computer. Putting all the components of a quantum computer together could prove really hard. System integration may be the ultimate challenge. Quantum information processing (QIP) will need to exploit standard silicon technology to run the quantum system; and QIP must work alongside a feasible laser optics system. The optical systems are seriously complicated, though each feature seems manageable. It may be necessary to go to architectures even more complicated than those I have described. It might even prove useful to combine elements of remote entanglement and optical spin control, whether this is regarded as using remote entanglement to link spin patches, or as having spin patches instead of ${\text{NV}}^{-}$ centers as nodes for remote entanglements. A short article like this has to miss out many features of importance, not least questions of error correction, but a major message is that, even in the most rudimentary approaches, we have to think through all of the system when talking of a possible computer.

And what would you do with a quantum computer if you had one? Proposals that do not demand room temperature range from probable, like decryption or directory searching, to the possible, like modeling quantum systems, and even to the difficult yet perhaps conceivable, like modeling turbulence. More frivolous applications, like the computer games that drive many of today’s developments, make much more sense if they work at ambient temperatures. And available quantum processing at room temperature would surely stimulate inventive new ideas, just as solid-state lasers led to compact disc technology.

Summing up, where do we stand? At liquid nitrogen temperatures, say $77\text{K}$, quantum computing is surely possible, if quantum computing is possible at all. At dry ice temperatures, say $195\text{K}$, quantum computing seems reasonably possible. At temperatures that can be reached by thermoelectric or thermomagnetic cooling, say $260\text{K}$, things are harder, but there is hope. Yet we know that small (say 2–3 qubit) quantum devices operate at room temperature. It seems likely, to me at least, that a quantum computer of say 20 qubits will operate at room temperature. I do not say it will be easy. Will such a QIP device be as portable as a laptop? I won’t rule that out, but the answer is not obvious on present designs.

This work was supported in part by EPSRC through its Basic Technologies program. I am especially grateful for input from Gabriel Aeppli, Polina Bayvell, Simon Benjamin, Ian Boyd, Andrea Del Duce, Andrew Fisher, Tony Harker, Andy Kerridge, Brendon Lovett, Stephen Lynch, Gavin Morley, Seb Savory, and Jason Smith. I am particularly grateful to Simon Benjamin and Stephen Lynch for preparing the initial versions of the figures.