A new twist in a ferromagnet
Generally speaking, one of the most fascinating aspects of physics is the emergence of complex structures out of simple laws, an interesting case of which are structures protected by topological invariants. To illustrate an example of this, consider vortex lines in superconductors. In such systems, the phase of the Cooper-pair wave function rotates by 2πn as one circles a vortex. Continuity then requires the vorticity n to be an integer. For this reason, a vortex with n=±1 cannot decay.
The intermetallic compound MnSi exhibits complex magnetic structures at low temperatures that many have suspected to be topologically nontrivial, that is, containing “knots” in the magnetization. So far, however, direct experimental evidence for this has been lacking. In two Letters appearing in Physical Review Letters, one by Christian Pfleiderer’s group at Technische Universität München and collaborators at Universität zu Köln [1], and Minhyea Lee and co-workers at Princeton, NJ, and collaborators at the University of Chicago and the University of Tokyo [2] report on measurements of the Hall effect in two different parts of the MnSi phase diagram, which provide such evidence.
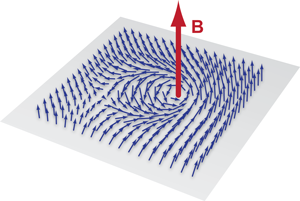
In magnetic systems, the vector character of the magnetization leads to more complex topological states. Figure 1 shows a sketch of the normalized magnetization ˆm=m/|m| for a so-called skyrmion in a two-dimensional magnet. The term skyrmion derives from the analogy with the Skyrme model for nucleons in pion field theory [3]. The magnetization points in the direction of the applied magnetic field far from the skyrmion, but in the opposite direction at its center. The magnetization rotates smoothly about a line through the center. Like a vortex in a superconductor, a skyrmion cannot be unwound without creating discontinuities.
Skyrmions have been discussed extensively in the context of the quantum Hall systems, which are two-dimensional electron gases at low temperatures [4]. It is interesting to observe skyrmions in the more conventional, three-dimensional magnetic system MnSi at higher temperatures.
MnSi shows long-range magnetic order below a critical temperature Tc≈29.5K. Partial spin polarization lowers the Coulomb energy of the electron gas, since the Pauli principle prevents electrons with the same spin from coming too close. This Stoner mechanism stabilizes ferromagnetism at low temperatures.
MnSi is however not quite ferromagnetic. The magnetization feels the crystal structure due to spin-orbit interactions. MnSi has a relatively complicated structure containing screw axes. This imparts a preferred screw sense on the magnetization. At low applied magnetic fields, the magnetization forms a spiral with a period of 190Å, which is aligned with a certain crystallographic axis. In the directions perpendicular to the spiral axis, the magnetization is uniform. The spiral is unpinned from the crystal axes and aligned in parallel to the magnetic field by a field of about 100mT. This allows the system to lower its energy by canting the magnetization towards the field direction. With increasing field, the canting increases, until, above about 550mT, the magnetization becomes completely aligned with the field.
However, this is not the whole story for MnSi. In the early 1980s, a new phase, the so-called A phase, was discovered at intermediate magnetic fields and close to Tc [5,6]. Experiments have suggested a nontrivial magnetic structure in the A phase, but its precise nature has remained controversial. Recent neutron-scattering experiments by Mühlbauer et al. [7], including the authors of Ref. [1], suggest a superposition of three spirals, oriented perpendicularly to the applied field and forming angles of 120∘ with each other. Their observations are consistent with a triangular lattice of skyrmions in the plane perpendicular to the field and with translational invariance along the field direction. Such states had been predicted [8–11], but not observed. However, while neutron scattering experiments [7] exhibit the translational symmetry of the magnetic state, they do not directly probe the topological state. The two Letters highlighted in this Viewpoint present Hall-effect measurements, one paper in the A phase [1] and the other under higher pressure [2], which address this question.
The Hall effect in MnSi contains contributions besides the ordinary Hall effect: the anomalous and topological Hall effects. The anomalous Hall effect is due to the nonvanishing average magnetization in an applied magnetic field. Neubauer et al. [1] observe another contribution to the Hall effect that is sharply restricted to the A phase. They show that a lattice of skyrmion lines would lead to a topological Hall effect, which can be described by an effective magnetic field proportional to the concentration of skyrmions. The observed contribution has the predicted magnitude and sign, strongly supporting the skyrmion picture for the A phase.
This does not close the case, though: Lee et al. [2] observe a much larger additional contribution to the Hall effect under applied pressures between 6 and 12kbar. It is known that increasing the pressure leads to a monotonic decrease of the critical temperature, which reaches zero at a pressure of pc≈14.6kbar. Above pc, neutron scattering indicates that spiral order persists on short length scales, whereas the spiral orientation is fluctuating [12]. Several groups have suggested that this partially ordered state is topologically nontrivial [9–11]. This state also shows unusual electronic transport properties [13,14].
Lee et al. [2] observe the additional contribution in a much larger range of temperature and magnetic field than where low-frequency susceptibility measurements find a stable A phase [15]. This suggests that fluctuating, not static, skyrmions might be present over a broad range of the phase diagram under pressure. However, it is not easy to understand the very large skyrmion density that would be required to explain the large additional Hall effect. Neutron scattering data for this pressure range are clearly required. They should help to determine how the purported fluctuations for p<pc are related to, on the one hand, the anomalous behavior above pc and, on the other, the skyrmion lattice at ambient pressure.
In any case, the large contribution to the Hall effect observed under pressure [2] shows that this contribution is not restricted to the A phase. Therefore, one would like to see independent confirmation of the proposed skyrmion structure of the A phase even at ambient pressure. Local probes, such as dedicated muon spin relaxation experiments, would be valuable, as would direct imaging, e.g., with a spin-polarized scanning tunneling microscope. It is likely that the topological magnetic states of MnSi will present us with more surprises.
References
- A. Neubauer, C. Pfleiderer, B. Binz, A. Rosch, R. Ritz, P. G. Niklowitz, and P. Böni, Phys. Rev. Lett. 102, 186602 (2009)
- M. Lee, W. Kang, Y. Onose, Y. Tokura, and N. P. Ong, Phys. Rev. Lett. 102, 186601 (2009)
- T. H. R. Skyrme, Proc. R. Soc. A 260, 127 (1961)
- Y. Gallais, J. Yan, A. Pinczuk, L. N. Pfeiffer, and K. W. West, Phys. Rev. Lett. 100, 086806 (2008) and references therein
- K. Kadowaki, K. Okuda, and M. Date, J. Phys. Soc. Jpn 51, 2433 (1982)
- Y. Ishikawa and M. Arai, J. Phys. Soc. Jpn. 53, 2726 (1984)
- S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii, and P. Böni, Science 323, 915 (2009)
- A. N. Bogdanov and D. A. Yablonskii, Sov. Phys. JETP 68, 101 (1989); A. Bogdanov and A. Hubert, J. Magn. Magn. Mater 138, 255 (1994)
- U. K. Rößler, A. N. Bogdanov, C. Pfleiderer, Nature 442, 797 (2006)
- B. Binz, A. Vishwanath, and V. Aji, Phys. Rev. Lett 96, 207202 (2006)
- I. Fischer, N. Shah, and A. Rosch, Phys. Rev. B 77, 024415 (2008)
- C. Pfleiderer, D. Reznik, L. Pintschovius, H. v. Löhneysen, M. Garst, and A. Rosch, Nature 427, 227 (2004)
- C. Pfleiderer, S. R. Julian, and G. G. Lonzarich, Nature 414, 427 (2001)
- C. Pfleiderer, P. Böni, T. Keller, U. K. Rößler, and A. Rosch, Science 316, 1871 (2007)
- C. Thessieu, C. Pfleiderer, A. N. Stepanov, and J. Flouquet, J.Phys.: Condens. Matter 9, 6677 (1997)