Too entangled to quantum compute one-way
Computers that exploit quantum effects appear capable of outperforming their classical brethren. For example, a quantum computer can efficiently factor a whole number, while there is no known algorithm for our modern classical computers to efficiently perform this task [1]. Given this extra computational punch, a natural question to ask is “What gives quantum computers their added computational power?” This question is intrinsically hard—try asking yourself where the power of a traditional classical computer comes from and you will find yourself pondering questions at the heart of the vast and challenging field known as computational complexity. In spite of this, considerable success has been made in answering the question of when a quantum system is not capable of offering a computational speedup. A particularly compelling story has emerged from the study of entanglement—a peculiar quantum mechanical quality describing the interdependence of measurements made between parts of a quantum system. This work has shown that a quantum system without enough entanglement existing at some point in the process of a computation cannot be used to build a quantum computer that outperforms a classical computer [2]. Since entangled quantum systems cannot be replicated by local classical theories, the idea that entanglement is required for speedup seems very natural. But now two groups [3,4] have published papers in Physical Review Letters that put forth a surprising result: sometimes too much entanglement can destroy the power of quantum computers!
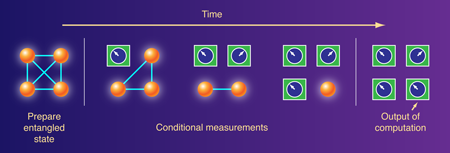
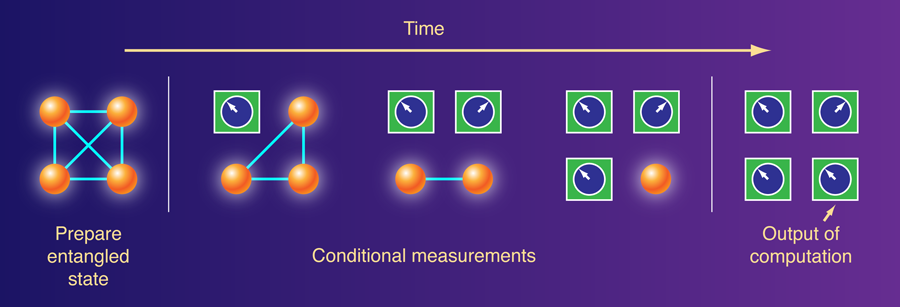
Both papers focus on a model called the “one-way quantum computer,” which was invented by Hans Briegel and Robert Raussendorf in 2001 [5]. A one-way quantum computation begins with a special quantum state entangled across many quantum subsystems, and the computation proceeds as a measurement is made on each subsystem. The actual form of each of the measurements in the sequence of measurements is determined by the outcome of previous measurements (Fig. 1), and one can think of the measurements as an adaptive program executed on the substrate of the entangled quantum state. A particularly nice property of the one-way quantum computing model is that it separates quantum computing into two processes—the preparation of a special initial quantum state and a series of adaptive measurements. In this way we may view the initial quantum state as a resource that can boost localized measurements and classical computation up into quantum realms. Investigations have revealed numerous quantum states that can be used as the special initial state to build a fully functioning quantum computer. But how special is this initial quantum state? Will any entangled quantum state do?
The two papers approach this problem from slightly different perspectives, but both arrive at convincing answers to these questions. David Gross at Technische Universität Braunschweig in Germany, Steven Flammia at the Perimeter Institute for Theoretical Physics in Waterloo, Canada, and Jen Eisert at the University of Potsdam, Germany, pursue this question directly in terms of entanglement [3]. They first show that if a certain quantification of entanglement—known as the geometric measure of entanglement—is too large, then any scheme that mimics the one-way quantum computation model cannot outperform classical computers. In fact, they show that the measurements in this case could be replaced by randomly flipping a coin, without significantly changing the effect of the computation. Thus while these states have a large amount of entanglement, they cannot be used to build a one-way quantum computer. Gross, Flammia, and Eisert also show that if one picks a random quantum state, it will, with near certainty, be a state that has a high value of geometric entanglement. The random states they consider are drawn via a probability distribution known as the Haar measure, which is the probability distribution that arises naturally when one insists that the probability of drawing a particular state not depend in any way on the basis of states one uses to describe a quantum system. Gross et al.’s findings show that not only do states that are too entangled to allow one-way quantum computation exist, they are actually generic among all quantum states.
Michael J. Bremner and Andreas Winter of the University of Bristol in the UK and Caterina Mora at the University of Waterloo in Canada take a slightly different route to finding states that are not useful for one-way quantum computation [4]. They begin by showing that a random quantum state (again drawn from the Haar measure) is not useful for one-way quantum computation with high probability, confirming the result of Gross et al. But they also show it is possible to choose a random quantum state from an even smaller class of states than the completely random quantum states and still end up with a state not useful for one-way quantum computation. This more limited class of states has even less entanglement (though still quite a lot) than those considered by Gross et al., but they can still be useless for one-way quantum computation.
The bottom line is that entanglement, like most good things in life, must be consumed in moderation. For the one-way quantum computation model, a randomly chosen initial state followed by adaptive measurements is not going to give you a quantum computer. Part of the reason for this, as revealed by Gross et al., is that a randomly chosen initial state has too much geometric entanglement. But even states with less entanglement may be useless for one-way quantum computation. All is according to the color of the crystal through which you look, however, one may naturally ask: What do all of these statements about the power of initial random quantum states have to do with the real world? It is thought, for example, that perfectly random quantum states (drawn from the Haar measure) cannot be produced efficiently on a quantum computer. So, while it may be that a perfectly random quantum state isn’t useful for one-way quantum computation, maybe the states that exist in nature, which can be constructed efficiently, actually are useful. It is known, for example, that the ground states of certain chains of interacting spins can be used for one-way quantum computation. A recent preprint by Richard Low [6] hints, however, that even states that exist in nature might also be in the class of useless states considered by Gross et al. and Bremner et al. In particular, Low has shown that there is a way to efficiently construct a class of entangled random quantum states that are not useful for one-way quantum computation. Thus the kinds of generic situations that both groups consider should not be ruled out because there is no physical model that efficiently prepares these states: quantum states that are impotent for one-way quantum computation may be the norm and not the exception. The implications for this on the viability of one-way quantum computation are probably not dire, but it does point out how special the states that can be useful for this model need to be—as well as the clever thinking needed to think this model up in the first place.
Finally, one can take a step back and ask “What are the implications of these results for understanding the source of the power of quantum computation?” Entanglement, in quite a real sense, is not the full answer to this question. The results of these two papers drill a deeper hole into the view of those who believe that the largeness of entanglement, and of entanglement alone, should be the useful discriminating factor between quantum and classical computation. From the perspective of theoretical computer science, this is not too surprising. One of the big open questions in this field is whether what is efficiently computable on a classical computer is the same as what is efficiently computable on a computer that operates according to different laws of the universe—a universe where a computer can nondeterministically branch (in computer science, this is known as the P versus NP question). This latter nondeterminism isn’t the kind a physicist normally thinks about. Instead it is a nondeterminism in which one can select out which of the nondeterministic branches of a universe one wishes to live in. This nondeterminism is not the way in which our universe appears to work, but it is one way the world could work (i.e., a possible set of laws of physics).
Trying to understand why our classical computers cannot efficiently compute what could be efficiently computed in these nondeterministic worlds is the holy grail of computer science research. The failure to solve this problem is similar to saying there is no known way to write down a quantity that succinctly quantifies why modern computers are different from computers that exist in the nondeterministic world. We should not be surprised, then, if there is no way to write down a quantity that quantifies why a quantum computer is powerful. After all, quantum physics is just another set of laws that operate differently than classical laws. While it is easy to view this through a negative lens, in actuality it should provide the wind behind research into quantum algorithms: there is still much to be discovered about where quantum computers might offer computational advantages over classical computers. Just be aware that creating too much entanglement followed by a series of measurements may not be the best way to get the answer.
References
- P. W. Shor, in Proceedings of the 35th IEEE Annual Symposium on the Foundations of Computer Science, Santa Fe, New Mexico, 1994, edited by S. Goldwasser (IEEE Press, Los Alamitos, 1994), p. 124
- R. Jozsa and N. Linden, Proc. R. Soc. London A 459, 2011 (2003)
- D. Gross, S. T. Flammia, and J. Eisert, Phys. Rev. Lett. 102, 190501 (2009)
- M. J. Bremner, C. Mora, and A. Winter, Phys. Rev. Lett. 102, 190502 (2009)
- R. Raussendorf and H. J. Briegel, Phys. Rev. Lett. 86, 5188 (2001)
- R. Low, arXiv:0903.5236 (2009)