Optomechanics

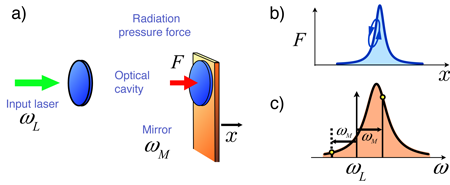
The typical experimental setup in optomechanics consists of an optical cavity where one of the end-mirrors can move (Fig. 1). For example, experimentalists have attached micromirrors to atomic force microscope cantilevers or doubly clamped beams [8–10]. When the cavity is illuminated by a laser, the circulating light gives rise to a radiation pressure force that deflects the mirror. Any displacement of the mirror will, in turn, change the cavity’s length, shifting the optical cavity mode frequency with respect to the fixed laser frequency, and thereby alter the circulating intensity. It is this coupled dynamics that produces a wealth of interesting effects in such systems.

×

The role of the cavity is twofold: It resonantly enhances the circulating intensity, and it makes the intensity depend very sensitively on the position. Although the setup described here may seem rather special at first, it is in fact just one incarnation of a very generic nonlinear nonequilibrium situation: On the most general level, we are dealing with a resonance (the optical cavity mode) that is driven (by a laser), and whose resonance frequency is pulled by the displacement of some mechanical degree of freedom (the movable mirror). Having the resonance frequency depend in this manner on the position immediately implies that there will be a mechanical force. Given this general description, it is no wonder the same physics has by now been realized in a diverse variety of physical systems, including superconducting microwave circuits [12] and ultracold atoms [24,25]. However, in the following we will employ the terms appropriate for a simple optical setup, keeping in mind that the concepts can readily be translated to other situations.

Intrinsically, the movable mirror is a harmonic oscillator. However, as the radiation force depends on the mirror’s position, it modifies the mechanical properties of the mirror. The force gradient will change the mirror’s spring constant, creating an “optical spring” effect, which has been used to increase the frequency of a mirror by a factor of more than $20$, essentially trapping it using light [6]. The potential in which the mirror moves can be changed drastically by the radiation forces, eventually giving rise to multiple stable positions if the circulating intensity is large enough [26].

There is yet another crucial feature about the radiation forces: they respond with a time lag. In the setup discussed here, this is due to the finite ring-down time of the cavity, i.e., the time needed for photons to leak out (proportional to the cavity’s “finesse” or quality factor). The radiation force as a function of mirror position is a simple Lorentzian (known as the Fabry-Pérot resonance). Let us imagine that the mirror is placed on the slope of the resonance (see panel b of Fig. 1). As the mirror oscillates, e.g., due to thermal fluctuations or because it is driven by a laser, it moves back and forth along the slope. On approaching the resonance, the force will be smaller than expected, due to the time lag, and it remains larger when the mirror retracts. Overall, the radiation force extracts work from the mirror: $\oint Fdx<0$. This amounts to an extra damping, which will cool down the mirror by reducing thermal fluctuations. As discussed below, positioning the mirror on the opposite side of the resonance leads to a negative effective damping constant and hence to parametric amplification of the response to applied forces (and thermal fluctuations). These effects are sometimes labeled “dynamical backaction,” since they involve the light field acting back on the mechanical motion after having been perturbed by the mirror. Alternative optomechanical cooling schemes include Doppler-cooling in Bragg mirrors [27] and “active feedback cooling” [10,23,28].

The optomechanical damping rate ${\mathrm{\Gamma }}_{\text{opt}}$ scales linearly with laser intensity and depends sensitively on the position of the mirror. In the naive classical picture described here, it reduces the effective temperature according to $T_{\text{eff}}=T\mathrm{\Gamma }/(\mathrm{\Gamma }+{\mathrm{\Gamma }}_{\text{opt}})$, where $T$ is the bulk equilibrium temperature and $\mathrm{\Gamma }$ is the intrinsic mechanical damping rate. Note that we are talking about the effective temperature of a single mechanical mode of the structure that carries the mirror: Optomechanical cooling will not reduce the bulk temperature of the setup. This, however, is fully sufficient, if in the end the experiment is only sensitive to this particular degree of freedom. An analogous situation arises in matter wave interferometers using molecules, where the center-of-mass motion may be quantum, even though the internal motion of atoms in the molecule remains hot.

The classical time delay description given above shows how the viscous damping force is produced. As we move to the full quantum picture, it is convenient to switch from the time domain to the frequency domain. Periodic motion of the mechanical system at frequency ${\omega }_M$ leads to amplitude and phase modulation of the optical amplitude inside the cavity. This modulation leads to sidebands displaced from the optical carrier frequency by $\pm {\omega }_M$. This is precisely analogous to Raman scattering from a solid whose index of refraction is periodically modulated in time (and space) by sound waves. Hence, just as in Raman spectroscopy, these lower and upper sidebands are referred to as Stokes and anti-Stokes signals respectively. If both phase and amplitude modulation are present, they interfere causing one sideband to be stronger than the other. This can be achieved by detuning the optical carrier frequency from the cavity resonance.

Quantum mechanically, the lower sideband comes from a process in which a carrier photon loses energy $\mathrm{ħ}{\omega }_M$ by creating a phonon inside the mechanical oscillator. Correspondingly the anti-Stokes upper sideband comes from a process that removes energy $\mathrm{ħ}{\omega }_M$ from the mechanical oscillator. This is the process needed for cooling. Because the sideband photons differ in energy by $2\mathrm{ħ}{\omega }_M$, a difference in intensity of the two sidebands implies a net energy transfer by the optical field from or to the mechanical system. The required asymmetry is achieved by putting the optical carrier frequency below the nominal cavity Fabry-Pérot resonance. As shown in panel c of Fig. 1, this puts the anti-Stokes line closer to the cavity resonance and the Stokes line further away. This yields an asymmetry in the density of states seen by the Stokes and anti-Stokes photons and hence an asymmetry in the rate of their production, as can be analyzed nicely in the “quantum noise” approach [19,29].

Although this scheme produces cooling, we cannot approach the quantum ground state unless the Stokes intensity is close to zero. This is reasonable since the Stokes process excites the mechanical system to higher energy levels. As shown in Fig. 1 (panel c), the huge Stokes/anti-Stokes asymmetry can be achieved only in the “good cavity” limit where the cavity resonance linewidth is smaller than the sideband spacing $2\mathrm{ħ}{\omega }_M$. Another condition is that the optical intensity be high enough that the resulting optical damping almost instantly removes any thermal phonons that enter the mechanical oscillator from the surroundings. Then, the full quantum expression for the minimum achievable mean phonon number of the oscillator is [29,30]

where $\kappa$ is the optical ring-down rate of the cavity. While not technically easy, one can in principle detect the approach to the mechanical ground state by the disappearance of the anti-Stokes sideband. Mechanical and optical resonances hybridize [29,31] in the strong-coupling regime when ${\mathrm{\Gamma }}_{\text{opt}}$ exceeds the cavity decay rate $\kappa$.

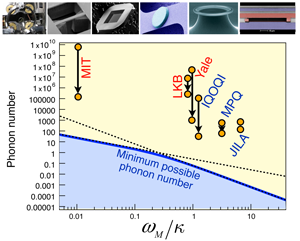
At present, experiments have not yet reached the ground state, though phonon numbers as low as $30$ have been obtained very recently using optomechanical cooling [32,33]. Current challenges include starting from a low bulk temperature (requiring cryogenic operation), ensuring a large mechanical quality factor (which limits the achievable cooling ratio), and fighting spurious heating from light absorption. Figure 2 illustrates the current status for intrinsic cooling (without feedback).

×

Detecting the mirror’s motion is in principle straightforward, since the optical phase shift is directly proportional to the mirror’s displacement $x$. Typically, the Lorentzian frequency spectrum of the mirror’s position fluctuations is obtained in this way. The peak width yields the total damping rate, including the effective optomechanical damping. The area under the spectrum reveals the variance of $x$, which is a measure of the effective temperature, according to the classical equipartition theorem.

It is well known that quantum mechanics puts a fundamental constraint on the sensitivity of any such “weak” displacement measurement [18,19]. Indeed, being able to follow the motion over time with arbitrary precision would reveal the mirror’s trajectory, which is forbidden by Heisenberg’s uncertainty relation. The photon shot noise limits the precision for estimating the phase shift. In principle, this can be overcome by increasing the light intensity. However, then another effect kicks in: The shot noise of photons being reflected from the mirror imprints an unavoidable “jitter,” masking the mirror’s “intrinsic” motion. This effect is called measurement backaction. The standard quantum limit is reached when both effects are equally strong. It corresponds to resolving the mirror’s position to within its ground state uncertainty, after averaging the signal over a damping time. The quantum limit has been approached up to a factor of $5$ recently [33], with an imprecision of ${10}^{-18}m/\sqrt{\text{Hz}}$. Detecting the measurement backaction effects is still an outstanding challenge (but see Ref. [35]). Backaction free measurements of one of the two quadratures (cosine or sine oscillatory components) of the mechanical motion [36] are another option.

However, in order to see genuine “quantum jumps,” it is necessary to carry out a quantum nondemolition measurement with respect to an observable that, unlike position, is conserved by the Hamiltonian. The most important example in this context would be the phonon number. Recently, a modified optomechanical setup was introduced [15,37], with a movable membrane in between two fixed end-mirrors. In such a situation, the optical frequency shift can be made to depend quadratically on the displacement. This would enable phonon number (Fock state) detection, once the parameters are optimized further and the system can be cooled into the quantum regime.

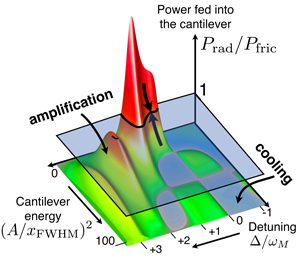
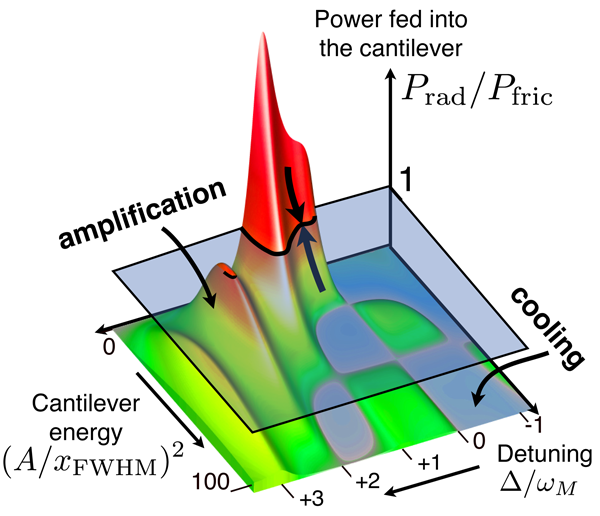
Beyond the linearized dynamics discussed up to now, such systems can display much richer, nonlinear effects as well. Recall that on the decreasing slope of the force vs position curve, work is performed on the mirror, effectively reducing the overall damping as ${\mathrm{\Gamma }}_{\text{opt}}$ now becomes negative. Once the laser intensity is strong enough to make the total “damping rate” negative, any tiny amplitude oscillation will grow exponentially [38–40]. This growth finally saturates due to nonlinear effects, and the mirror settles into periodic, self-sustained oscillations, as observed in experiments [13,16,17]. Their amplitude is determined by the laser intensity, the detuning, and the strength of the intrinsic mechanical friction, as well as other parameters. Note that the parametric instability we have just described is conceptually identical to what happens in a laser above the lasing threshold. Here, the mechanical vibration plays the role of the laser’s light mode, and the pump is provided by the radiation that drives the cavity.

To obtain the attractors (i.e., steady-state solutions) for the motion, one may pose a simple question: How does the work per cycle performed by the radiation field depend on the mirror’s oscillation amplitude? The power fed into the system has to match the power dissipated by friction. When one draws a map of the possible amplitudes of oscillation that are consistent with this condition, an intricate structure emerges [40,41] (see Fig. 3). In particular, at fixed parameters a large number of possible amplitudes may exist simultaneously. This multistability has begun to be explored in experiments [17] and it might even be useful for sensitive measurements [40]. At even higher optical drive powers, the mirror may enter a state of chaotic motion [42], which still remains mostly unexplored. In addition, one may ask about possible quantum effects in the nonlinear dynamics [41].

×

The question arises how to use the optomechanical interaction to produce genuinely nonclassical states of the light field and/or the mechanical motion. As we have seen, the cavity length changes in response to the circulating intensity. In this regard, the setup is equivalent to a nonlinear optical medium, with an intensity-dependent index of refraction. Such a nonlinear medium may be used to produce squeezing in the light field, e.g., by suppressing the intensity fluctuations (amplitude squeezing), and this can be translated directly to the optomechanical response [43]. With regard to the mirror, squeezed states might be produced by varying the optical spring constant in time. As indicated above, mechanical Fock states could be produced via measurements.

Entanglement between the light field and the mirror can be generated easily, in principle. Suppose for a moment that the cavity is closed and the field is in a superposition of different photon numbers, e.g., in a coherent state. Each of these Fock states of the radiation field will exert a different radiation pressure force, thereby displacing the mirror by a different amount. This creates an entangled state, which may be called a “Schrödinger cat” state, as the mirror involves many billions of atoms (see, e.g., [44–47] and others). Remarkably, after a full period of the mirror oscillation, the entanglement would be undone, as in a quantum eraser experiment. It has been suggested that producing entanglement in this way and checking for its decay over time could eventually be a means to test for potentially unknown sources of decoherence, probably even including hypothetical gravitationally induced collapse of the wave function of the massive mirror [46]. When several movable mirrors or membranes are included, the radiation field can be exploited as a medium that couples these mechanical elements to each other [48–50], leading to entanglement if thermal fluctuations are sufficiently suppressed. Experimental proof of entanglement then requires correlation measurements via optical probe beams.

Among the setups that have been realized during the past five years, most involve cantilevers [7,10] or nanobeams [8,9] as mechanical elements. Masses typically range from ${10}^{-15}$ to ${10}^{-10}\text{kg}$ (and even $1\text{g}$ [6]), while frequencies are often in the MHz regime ( ${\omega }_M/2\pi$ = $1\text{kHz}$ to $100\text{MHz}$). Light is typically reflected from Bragg mirrors made from multi-layered dielectric materials. A rather different approach is based on microtoroid optical cavities made from silica on a chip [13,14,51]. The light circulating inside an optical whispering gallery mode inside the toroid exerts a radiation pressure that couples to a mechanical breathing mode. The biggest challenge in all of these devices is to obtain both a high optical finesse (currently in the range from ${10}^3$ to ${10}^5$), and a high mechanical quality factor ( ${10}^3$ to ${10}^5$ for beams and cantilevers). As explained above, an alternative approach [15,37] involving a membrane with a thickness of $50\text{nm}$ inside a fixed optical cavity can circumvent this problem to some degree, and has reached a finesse of ${10}^4$ and a mechanical quality factor of ${10}^6$.

Optomechanical ideas have recently been realized in a number of other systems as well. For example, it is possible to replace the optical cavity by driven radio-frequency [52] or microwave [12,34] circuits, whose resonance frequency depends on the motion of a capacitively coupled nanobeam. The setup involving superconducting microwave resonators is especially promising as it can be coupled to Josephson junctions, qubits, and amplifiers on the same chip. Incidentally, the essence of optomechanical cooling has also been demonstrated using a current-driven superconducting single electron transistor in place of the optical cavity [53].

Another recent development exploits a gradient optical force between dielectric structures, where the coupling is through the evanescent light field. The devices have scaled from glass fiber [54] down to integrated silicon nanobeams of picogram mass [55], and large forces can be generated without the need for a high finesse cavity. One may thus envisage integrating mechanical devices with photonic crystals, waveguides, and other optical elements on a chip, serving as the basis for optically controlled mechanical information processing and sensing.

For a long time, radiation forces had already been used to cool, trap, and manipulate atoms, before being applied to mechanical structures. It is therefore amusing to note that the concepts of optomechanics are being transferred back to the domain of cold atoms. Several experiments [24,25] have now demonstrated how the mechanical motion of clouds of ultracold atoms inside an optical cavity can couple to the light field and display the effects we have been discussing. Given the small mass of the atom cloud, the mechanical effects of a single photon can be significant. This allows us to study optomechanics in a new domain, perhaps even leading to observation of entanglement between an atomic ensemble and a nanomechanical system (e.g., Ref. [56]).

In the short term, experiments are racing towards the ground state of mechanical motion, to enable manipulation in the quantum regime. Achieving this goal would open the door towards possible applications, for example, in the area of quantum information processing. It would also permit us to answer fundamental questions, such as whether we understand decoherence processes in massive objects. Sensitive measurements (of displacement, mass, etc.) are another area where optomechanical systems will find applications, and while they do not urgently require going into the quantum regime, they could benefit from the improved sensitivity.

In the longer term, optomechanics may also be viewed as a light-mechanics interface to realize hybrid structures for (classical or quantum) information processing, switching or storage, in integrated photonic circuits on a semiconductor chip.

We acknowledge support by NSF through grants DMR-0653377 and DMR-0603369 (to S. M. G), as well as Emmy-Noether program grants NIM and SFB 631 (to F. M.).