Optical switching with cold atoms

Andrew  M. C. Dawes

Viewpoint

Optical switching with cold atoms

Andrew M. C. Dawes

Department of Physics, Pacific University, Forest Grove, OR 97116, USA

May 18, 2009• Physics 2, 41

Loading cold atoms into a hollow-core optical fiber enables all-optical switching with just several hundred photons.

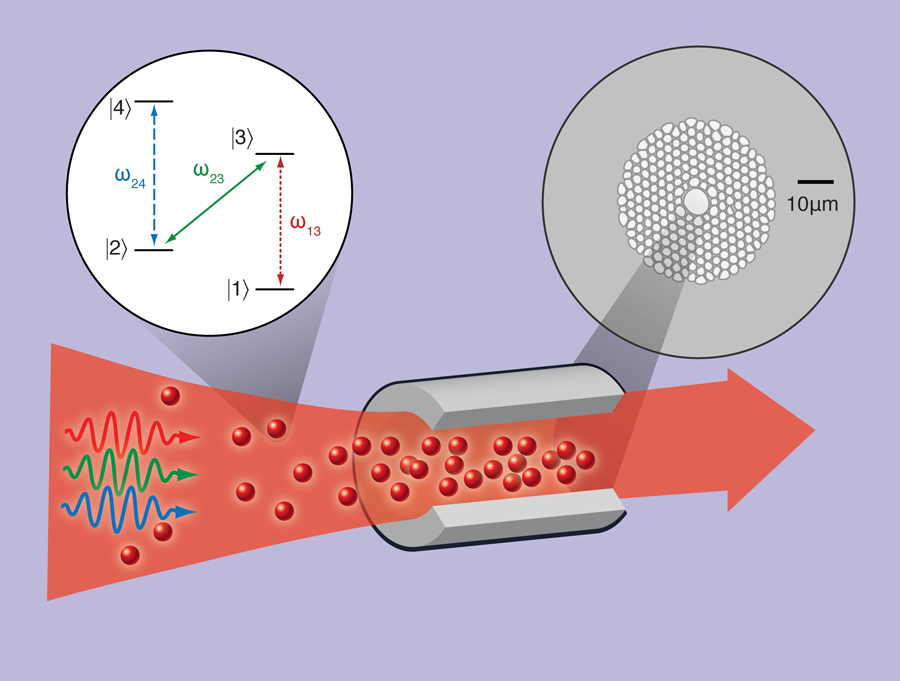
Figure caption — **Figure 1:** Rubidium atoms are loaded into and trapped within a hollow-core photonic crystal fiber. A cross section of the hollow fiber is shown in the upper right. A dipole trapping beam (large red arrow) serves to localize the atoms (red, not drawn to scale) within the hollow core of the fiber. Additional probe, coupling, and switch fields (red, green, and blue wave packets, respectively) can then control the atomic state and implement all-optical switching and electromagnetically induced transparency. The relevant atomic levels are indicated as states $| 1 〉$ , $| 2 〉$ , $| 3 〉$ , and $| 4 〉$ in the upper left. Note: the actual experimental orientation of the fiber is vertical to enable loading from a magneto-optical trap (not shown).

At room temperature and atmospheric pressure, atoms travel hundreds of meters per second and collide frequently with one another and their surroundings. Although this unceasing thermal motion keeps us warm, it causes serious problems for anyone trying to probe the internal state of an atom. To reduce the deleterious effects of atomic motion, experimentalists often rely on optical fields to trap and cool atoms [1]. In a paper appearing in Physical Review Letters [2], Michal Bajscy and colleagues at the Harvard-MIT Center for Ultracold Atoms demonstrate a system that is capable of trapping and cooling atoms and shuffling them into the tiny core of a hollow optical fiber (Fig. 1) The confined atoms are then in prime position to interact with beams of light guided by the fiber. This simultaneous confinement of light and atoms leads to increased optical nonlinearities with which the Harvard group can create an all-optical switch: a few hundred photons are capable of controlling the transmission of a weak ( $\sim 1 pW$ ) probe beam.

In a prototypical quantum information system, single photons transmit information. The control of one photon by another is typically mediated by a nonlinear interaction with atoms [3,4] and for this light-matter coupling to be strong requires a long interaction length and a high optical intensity. An optical beam in free space can only remain focused for a distance on the order of the Rayleigh range, given by $z_{R} = π w_{0}^{2} / λ$ , where $λ$ is the wavelength of light and $w_{0}$ is the narrowest radial size of the beam. This relationship shows that a large interaction length (large $z_{R}$ ) and a high intensity (small $w_{0}$ ) are not simultaneously possible with focused beams in free space. Waveguides, such as optical fibers, offer a straightforward way to increase both the interaction length and the optical intensity. The challenge for designing a quantum information system is therefore to combine a microscopic waveguide with a medium that exhibits large optical nonlinearities.

Photonic crystal fibers are a type of optical fiber where the core and cladding are a geometric arrangement of hollow voids that extend down the length of the fiber [5]. The voids are designed to satisfy the conditions for total internal reflection of light within the core. Hollow-core photonic crystal fibers, such as the one illustrated in the upper right inset of Fig. 1, are interesting because it is possible fill the few-micron-wide light-guiding core with a nonlinear optical material (see Ref. [6] for a recent review). Atomic vapors are particularly useful fiber mediums because optical nonlinearities can be enhanced near atomic resonances. The drawback is that resonant light experiences significant absorption. Electromagnetically induced transparency (EIT) is an improved technique based on quantum interference that renders the atomic medium transparent to resonant light while retaining the large and desirable nonlinear properties associated with the resonant response [7]. EIT has become a workhorse for quantum optics research, allowing slow- and fast-light [8], low-light all-optical switching [9,10], controlled storage and retrieval of single optical beams [11] and transverse images [12], among many other notable results.

In 2006, a group at Cornell showed that the optical intensity required to observe EIT decreases dramatically when warm rubidium atoms are confined within a fiber waveguide [6]. Of course, the thermal motion of warm atoms leads to Doppler broadening. Bajcsy et al. extend this prior work by loading cold rubidium atoms into an optical fiber. The loading process begins with a cloud of atoms confined by a magneto-optical trap, which is located above one end of a vertically aligned hollow-core fiber. An atom funnel, consisting of four current-carrying wires that create a magnetic field, guides the atoms, aided by gravity, from the initial cloud into the fiber.

Guiding atoms into the fiber is only part of the story. If the fiber were empty, the atoms would quickly adsorb to the fiber walls [13]. In order to prevent atomic adsorption, and to keep the atoms localized within the waveguide, Bajcsy et al. implement a dipole trap along the fiber axis (Fig. 1). This trap exists throughout the length of the fiber and extends upward toward the initial atom cloud. Dipole traps operate by applying an intensity-dependent force on each atom, which is attractive when the optical frequency is tuned below an atomic resonance (red-detuned). Within the waveguide, the region of large optical intensity is along the axis of the fiber, attracting the atoms away from the walls.

There are two drawbacks to using a dipole trap: the intense off-resonance field broadens the atomic resonance line shape and shifts the resonant frequency. Fortunately, both effects can be avoided by pulsing the dipole trapping field with a pulse period that is shorter than the time a typical atom will spend in the trap: the trap is rapidly turned off and on before the atoms have a chance to leave. The probe beams are then modulated in a similar way, but out of phase, so as to only sample the atoms when the dipole-trapping field is off.

With atoms loaded into the waveguide, Bajcsy et al. demonstrate several nonlinear optical effects. First, they show that light resonant with one atomic transition increases the absorption on a separate transition. The effect is simply due to the movement of atoms between the accessible energy levels. Atoms initially in the ground state $| 1 〉$ (left inset of Fig. 1) are excited to the state $| 3 〉$ . Once excited, the atoms can decay to a lower energy state $| 2 〉$ that is not the original ground state, increasing the population of state $| 2 〉$ and the absorption of light resonant with the $| 2 〉 \to | 4 〉$ transition (we will refer to such resonant light as having frequency $ω_{24}$ ). The transmission of a signal—specifically a beam of light with frequency $ω_{24}$ —can be reduced by $50 %$ by injecting 300 photons of frequency $ω_{13}$

In addition to demonstrating an all-optical switch based on incoherent population transfer, Bajcsy et al. observe EIT with similarly low light levels. EIT utilizes a strong field with frequency $ω_{23}$ to create a quantum interference between states $| 2 〉$ and $| 3 〉$ that prevents single-photon absorption between levels $| 1 〉$ and $| 3 〉$ . This quantum interference opens a transparency window for optical frequencies near $ω_{13}$ . With a coupling field pulse containing $\sim 6000$ photons, $60 %$ transmission can be achieved in the EIT window.

EIT can also be the basis for creating an all-optical switch. Initially proposed in 1998 by Harris and Yamamoto [14], the EIT-switching scheme has been successfully implemented in several systems [15,16,9,10]. By adding a fourth energy level $| 4 〉$ to the EIT scheme described above, light incident on the atoms with frequency $ω_{24}$ will destroy the quantum interference between states $| 2 〉$ and $| 3 〉$ , and thus allow absorption of light with frequency $ω_{13}$ . Injecting “switch” photons with frequency $ω_{24}$ can therefore control the absorption of an optical signal with frequency $ω_{13}$ . With 700 switch photons, Bajcsy et al. demonstrate a $50 %$ reduction of the initial transmission. Previous work on EIT switching in cold atoms has achieved this level of control using $\sim 20$ photons per pulse, but at the cost of significantly more powerful coupling fields [10]. The most notable difference between these results is that with an atom-filled fiber the coupling fields can be very weak—on the order of several thousand photons.

There are a number of other different approaches to all-optical switching, such as those based on controlling the orientation of patterns generated in nonlinear optical systems. A recent review of this approach shows that a pattern-based device implemented in rubidium vapor may not be able to operate below $\sim 400$ switch photons, and requires $\sim 2000$ switch photons to achieve $50 %$ signal reduction [17]. The fact that this result is similar to that obtained by Bajcsy et al. with such a different system may indicate a fundamental limit to all optical switching, but it is reasonable to expect that a modest improvement in the atom loading process will improve the sensitivity of an atom-filled fiber system in the near future.

The possibility of tightly confining atoms and photons to a small region of space will allow a wide range of nonlinear optical experiments. One particularly exciting possibility is the opportunity to observe novel many-body effects where individual photons interact with one another via nonlinear interactions in atomic media. Even though photons are bosons, one recent proposal suggests that they may undergo “fermionization” if they are confined to a one-dimensional waveguide such as the one discussed here. This transition corresponds to a novel state where photons behave as impenetrable particles and optical pulses separate into a crystal of nonoverlapping photons [18]. There is much new physics to be explored as atoms and photons are forced to interact strongly, and we may soon see single photons interacting with one another in nonlinear optical systems.

References

V. Letokhov, Laser Control of Atoms and Molecules (Oxford University Press, New York, 2007)[Amazon][WorldCat]
M. Bajcsy, S. Hofferberth, V. Balic, T. Peyronel, M. Hafezi, A. S. Zibrov, V. Vuletic, and M. D. Lukin, Phys. Rev. Lett. 102, 203902 (2009)
D. Bouwmeester, A. K. Ekert, and A. Zeilinger, The Physics of Quantum Information: Quantum Cryptography, Quantum Teleportation, Quantum Computation (Springer, New York, 2000)[Amazon][WorldCat]
L. M. Duan, M. D. Lukin, J. I. Cirac, and P. Zoller, Nature 414, 413 (2001)
R. F. Cregan, B. J. Mangan, J. C. Knight, T. A. Birks, P. St. J. Russell, P. J. Roberts, and D. C. Allan, Science 285, 1537 (1999)
S. Ghosh, A. R. Bhagwat, C. K. Renshaw, S. Goh, A. L. Gaeta, and B. J. Kirby, Phys. Rev. Lett. 97, 023603 (2006)
S. E. Harris, Phys. Today 50, 36 (1997)
R. W. Boyd and D. J. Gauthier, in Progress in Optics 43, edited by E. Wolf (Elsevier, Amsterdam, 2002), Ch. 6, p. 497[Amazon][WorldCat]
D. A. Braje, V. Balić, G. Y. Yin, and S. E. Harris, Phys. Rev. A 68, 041801 (2003)
J. Zhang, G. Hernandez, and Y. Zhu, Opt. Lett. 32, 1317 (2007)
D. F. Phillips, A. Fleischhauer, A. Mair, R. L. Walsworth, and M. D. Lukin, Phys. Rev. Lett. 86, 783 (2001)
P. K. Vudyasetu, R. M. Camacho, and J. C. Howell, Phys. Rev. Lett. 100, 123903 (2008)
E. B. Alexandrov, M. V. Balabas, D. Budker, D. English, D. F. Kimball, C. H. Li, and V. V. Yashchuk, Phys. Rev. A 66, 042903 (2002)
S. E. Harris and Y. Yamamoto, Phys. Rev. Lett. 81, 3611 (1998)
M. Yan, E. G. Rickey, and Y. Zhu, Phys. Rev. A 64, 041801 (2001)
Y. Chen, Z. Tsai, Y. Liu, and I. A. Yu, Opt. Lett. 30, 3207 (2005)
A. M. C. Dawes, D. J. Gauthier, S. Schumacher, N. H. Kwong, R. Binder, and A. L. Smirl, Laser & Photon. Rev. 3, (2009)
D. Chang, V. Gritsev, G. Morigi, V. Vuletić, V. M. Lukin, and E. Demler, Nature Phys. 4, 884 (2008)

About the Author

Andrew Dawes is an Assistant Professor of Physics at Pacific University in Forest Grove, Oregon. He received his Ph.D. from Duke University in 2008. His general research interests are in nonlinear and quantum optics. His recent projects include exploring novel geometries for cooling and trapping rubidium, pattern-forming nonlinear optics, and developing nanoplasmonic materials for use as biological sensors. In addition to his research efforts, he is involved with the development and implementation of innovative methods for teaching undergraduate physics.