Viewpoint: Fluctuations in open systems

Fluctuation theorems (FTs) establish fundamental identities about energy exchanges between a nonequilibrium system and its environment. Interest in such relations has been boosted by the possibility of applying perturbations to mesoscopic systems undergoing irreversible processes. While most recent research focused on classical systems, in a paper in Physical Review Letters, Michele Campisi, Peter Talkner, and Peter Hänggi, at the University of Augsburg in Germany, have now [1] extended FTs to open quantum systems, paving the way for further progress in scenarios ranging from Bose-Einstein condensates to metallic nanowires.

When in contact with a thermal bath, a system in thermodynamic equilibrium can be pushed off equilibrium by time-dependent external forces. For slow enough perturbations this process is quasistatic or reversible, i.e., the system evolves through a succession of equilibrium states and the total amount of work done by external forces equals the equilibrium free-energy difference between the initial and final states.

In 1997, Chris Jarzynski, then at the Los Alamos National laboratory, found a remarkable result for nonequilibrium scenarios [2]. According to the second law of thermodynamics, the total work is more than the reversible work: the difference between actual work and reversible work is equal to the net heat produced by dissipative forces and transferred from a system to the bath. Let W be the mechanical work due to external agents and let $\mathrm{\Delta }G$ denote the reversible work or free-energy difference. Jarzynski found that, for arbitrary irreversible processes,

where <…> is an average over an infinite number of trajectories (i.e., realizations of the irreversible process), $k_B$ is the Boltzmann constant, and $T$ is the temperature of the environment. The reversible process is a particular case of this relation where $W=\mathrm{\Delta }G$. With the Jarzynski equality we can obtain free-energy differences from measurements of the irreversible work, a possibility overlooked by most thermodynamics textbooks!

Hummer and Szabo subsequently emphasized the possibility of using the Jarzynski equality to extract the molecular potential of the mean force from nonequilibrium pulling experiments in biomolecules [3]. The first experimental test of the Jarzynski equality came about a year later from Bustamante and colleagues at UC Berkeley, who measured work exerted on a small RNA hairpin by repeatedly unzipping the molecule with optical tweezers [4]. Gavin Crooks, also at UC Berkeley, went further and found a relation between work distribution measured along a given (forward) protocol and its time-reversed counterpart, thus generalizing the Jarzynski equality [5],

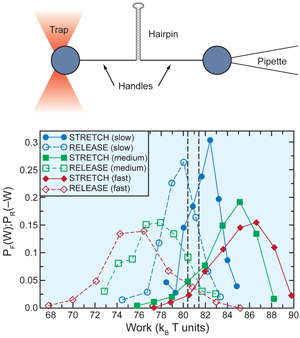
where $P_F(W)$ stands for the probability distribution of work along the forward process, $P_R(-W)$ is the distribution along the reverse process (the minus sign accounts for the change in sign of the displacement measured along the reverse process), and $\mathrm{\Delta }G$ equals the free-energy difference between the initial and final states along the forward process. In 2005 the Crooks relation was experimentally tested in mechanical unzipping/rezipping experiments with short RNA hairpins [6]. These and other results have recently stimulated a wealth of theoretical, experimental, and numerical research. To date several experimental tests of Crooks and related FTs have been carried out in beads captured in optical traps [7], mechanical and electrical oscillators [8], athermal systems [9], or in the recovery of full free-energy branches in DNA hairpins [10] (Fig. 1).

Fluctuation theorems are expected to be relevant for small systems where energy fluctuations are of the order of a few $kT$ [11] and for the Crooks FT, in particular, where ($W-\mathrm{\Delta }G)/k_{B}T$ is not too large and work fluctuations are measurable. In living systems nonequilibrium “machines” operate with a formidable efficiency in thermal environments despite intereference from Brownian motion of water molecules. By describing the spectrum of energy fluctuations of small objects along nonequilibrium processes, FTs offer insight into constraints biological machines must overcome to operate in a thermal environment. Such knowledge might be useful to design nanomachines that could operate in noisy environments with an efficiency comparable to that found in nature.

All these results belong to the domain of classical systems. Extending FTs to quantum systems would allow us to explore energy fluctuations in the arguably more interesting quantum domain. In 2000, Hal Tasaki [12] derived a Crooks-like relation for closed quantum systems (i.e., systems where the total energy is conserved). Subsequent attempts to extend the quantum FT to open systems were restricted to the weak-coupling (between the system and an external bath) case. Meanwhile, Jarzynski also showed how the equality he had previously derived for closed systems retained its validity for arbitrarily open classical systems [13]. In their recent paper, Campisi et al. [1] have closed the gap by extending the Tasaki-Crooks relation to arbitrarily open quantum systems. Using a natural decomposition of the joint partition function of the system in a bath, the authors recover Eq. (2) in terms of the quantum free energy of the system.

Is it possible to experimentally test the quantum FT? Testing a quantum FT is tantamount to measuring the mechanical work and the free-energy difference of the system between the initial and final states. Campisi et al. [1] define the free energy of a system as the difference between the total free energy of the system plus the bath and the bath-only free energy. Similarly to what is done in differential scanning calorimetry, one could devise a method in which the sample includes the system plus the bath, while the reference is the bath alone. A differential scan of both the sample and the reference should provide a measure of the free energy of the system alone. An a priori determination of the free-energy difference is not essential to test Eq. (2). To test the validity of the quantum version of Eq. (2) we should measure the quantum mechanical work distribution over many realizations of the quantum irreversible process.

And herein lies the greatest difficulty. How do we measure the work $W$ along a single trajectory? In contrast to classical systems, the measurement process of the work along a single trajectory interferes with the quantum dynamics itself. Crooks recently offered a clue about how this issue might be resolved [14]. Because the energy difference along a trajectory $\mathrm{\Delta }E$ is the sum of work $W$ and heat $Q$, we could infer the work by first measuring $\mathrm{\Delta }E$ and then $Q$ without interfering with the trajectory.

Is this possible? Measuring the energy difference between the initial and final states along a trajectory should not interfere with the dynamics. As the system starts out in equilibrium (i.e., in a mixture of pure states), the collapse of the wave function induced by the initial observation will preserve the initial Boltzmann-Gibbs measure. Moreover, we could measure the heat transferred to the bath. For a large enough bath, this should not interefere with the system dynamics. However, the whole issue remains unclear as we face a subtle problem of quantum measurement in interacting systems.

One can think of many possible scenarios to test quantum FTs: a Bose-Einstein condensate; a molecular magnet with macroscopic quantum tunneling; Josephson junctions; a metallic nanowire; shot-noise measurements in electronic devices. Unfortunately we don’t know which kind of experiment would yield the most reliable results. The advantage of quantum FTs as compared to classical FTs is that quantum systems need not be small or microscopic for quantum fluctuations to be measurable. The condensed matter experimentalist would likely start with quantum systems where current instrumentation allows for accurate measurement of quantum noise and thermodynamic free-energy differences. The next step would likely be the experimental measurement of work distributions in irreversible quantum systems . To paraphrase Lord Kelvin: Until you can measure something and express it in numbers, you have only the beginning of understanding. This seems to be more true than ever for quantum FTs.

References

1. M. Campisi, P. Talkner, and P. Hänggi, Phys. Rev. Lett. 102, 210401 (2009).
2. C. Jarzynski, Phys. Rev. Lett. 78, 2690 (1997).
3. G. Hummer and A. Szabo, Proc. Nat. Acad. Sci. 98, 3658 (2001).
4. J. Liphardt, S. Dummont, S. B. Smith, I. Tinoco, and C. Bustamante, Science 296, 1833 (2002).
5. G. E. Crooks, Phys. Rev. E 60, 2721 (1999).
6. D. Collin, F. Ritort, C. Jarzynski, S. B. Smith, I. Tinoco, and C. Bustamante, Nature 437, 231 (2005).
7. G. M. Wang, E. M. Sevick, E. Mittag, D. J. Searles, and D. J. Evans, Phys. Rev. Lett 89050601 (2002).
8. E. Garnier and S. Ciliberto, Phys. Rev. E 71, 060101 (2005); F. Douarche, S. Ciliberto, and A. Petrosyan, J. Stat. Mech.: Theor. Exp. P09011 (2005).
9. S. Schuler, T. Speck, C. Tierz, J. Wrachtrup, and U. Seifert, Phys. Rev. Lett. 94, 180602 (2005).
10. I. Junier, A. Mossa, M. Manosas, and F. Ritort, Phys. Rev. Lett. 102  070602 (2009).
11. C. Bustamante, J. Liphardt, and F. Ritort, Phys. Today 58, 43 (2005).
12. H. Tasaki arXiv:cond-mat/0009244 (2000).
13. C. Jarzynski, J. Stat. Mech.: Theor. Exp. P09005 (2004).
14. G. E. Crooks, J. Stat. Mech.: Theor. Exp. P10023 (2008).
15. A. Mossa, M. Manosas, N. Forns, J. M. Huguet, and F. Ritort, J. Stat. Mech.: Theor. Exp. P02060 (2009).