Observing unification on a grand scale

Aaron Pierce

Viewpoint

Observing unification on a grand scale

Michigan Center for Theoretical Physics (MCTP),Department of Physics, University of Michigan, Ann Arbor, MI 48109, USA

May 26, 2009• Physics 2, 44

New connections have been made between experimental astrophysical signatures and theories that unify the electromagnetic, weak, and strong forces, called grand unified theories.

Figure caption — **Figure 1:** Future data from three disparate sources— $TeV$ cosmic rays, big bang nucleosynthesis, and high-energy colliders—might also converge to give indications of GUT-scale physics.

Maurice Goldhaber placed an early limit on proton decay, noting that if protons had a lifetime shorter than $10^{17}$ years, you would “feel it in your bones.” That is, the radiation from these decays in your body would provide a fatal radiation exposure. The limits on proton decay have greatly improved since then. For some decay modes, the limits from the Super-Kamiokande experiment now exceed $10^{33}$ years [1], a limit only made possible by observing a tank of water with approximately $10^{34}$ protons in it. Why look so hard for such a rare process? Decay rates are suppressed by the masses of the particles responsible for mediating the decay. So, long lifetimes probe large energy scales.

For example, in the case of the proton, the symmetry that is responsible for its stability—conservation of baryon number—may only be approximate. Just such a violation of baryon number occurs at scales near $10^{16} GeV$ in “grand unified theories” (GUTs), theories that seek to unify electromagnetism, the weak and strong forces, but not gravity. This enormous energy scale translates into proton lifetimes close to the current bounds. So, if a very rare proton decay is observed, we will be probing high energy scales, indeed.

Work by Asimina Arvanitaki of the University of California, Berkeley, and colleagues at Stanford University in the US, appearing in the current issue of Physical Review D [2], points out that in a broad class of grand unified theories, there are additional ways to probe this large energy scale. Their starting point is supersymmetric theories. These theories posit a doubling of those particles that comprise the standard model, with far reaching consequences: these theories contain an excellent candidate for dark matter [3] and can stabilize the weak scale ( $M_{w} \sim 100 GeV$ ) against quantum corrections that might drag it up to the Planck scale ( $M_{pl} \sim 10^{18} GeV$ ). Perhaps most significantly, these theories quantitatively modify how the strength of the forces change with energy. If the strength of the known forces (excluding gravity) are extrapolated to high energies using calculations within the standard model, nothing particularly surprising occurs. With supersymmetry, this changes. In the simplest supersymmetric extension of the standard model, the “minimal supersymmetric standard model,” the lines parameterizing the strength of the three known forces meet at a single point, corresponding to an energy of $2 \times 10^{16} GeV$ [4]. At this energy, the known forces might unify. Thus supersymmetric theories provide a natural home for grand unification.

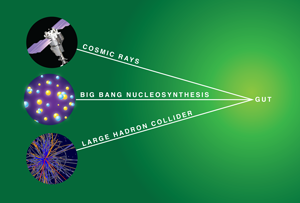
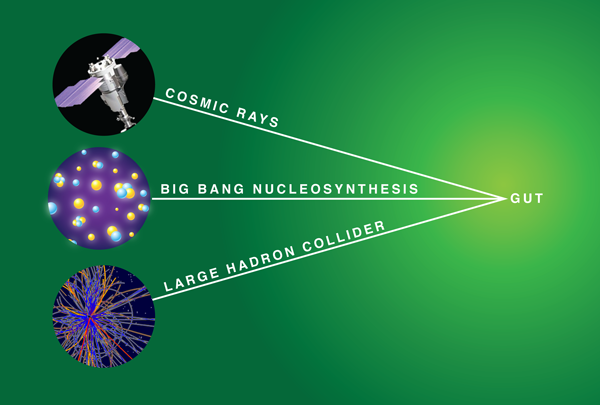
There is no guarantee that nature has chosen the simplest of supersymmetric theories, and minor modifications in the theory can make a big difference in its observable consequences. Arvanitaki et al. demonstrate that certain supersymmetric GUTs have exciting predictions in three a priori unrelated realms: the Large Hadron Collider (LHC), big bang nucleosynthesis (BBN), and cosmic rays. Combining the measurements from these sources may help to establish physics that operates at very high energies indeed (see Fig. 1).

It is the unique nature of dark matter in these theories that makes cosmic rays an important way to probe them. In these theories the dark matter can decay. This is in contrast to the simplest supersymmetric GUT, where the dark matter is comprised of the lightest supersymmetric particle, which is taken to be absolutely stable. Its infinite lifetime is ensured by a symmetry called R parity. However, as Arvanitaki et al. point out, minor modifications to the GUT could make the symmetry that ensures the longevity of the dark matter an approximate one. Then, just as violation of baryon number might induce proton decay with a lifetime of $10^{33}$ years, the dark matter might naturally decay with a lifetime of roughly $10^{19}$ years. Clearly, most of the dark matter will not have decayed—the universe is only $10^{10}$ years old—but the tiny fraction that does decay does so spectacularly, with decay products possessing hundreds of $GeV$ in energy. So, $10^{19}$ years turns out to be an important number, for as the authors emphasize, there are a variety of existing and upcoming cosmic-ray experiments that are capable of observing energetic decay products of dark matter, should it possess this lifetime. Depending on the precise route that dark matter takes to decay, experiments might observe an excess of gamma rays, neutrinos, positrons, or antiprotons. While the interpretation of these experiments can be complicated by astrophysical backgrounds, there is hope that features in the spectra of these decay products might be enough to conclude that it is truly the decay of dark matter that is being observed. Recent data from the PAMELA and Fermi experiments [5], e.g., have already caused quite a buzz, even if their interpretation remains unclear. If multiple dark matter decay channels are observed, the relative rates might be a window onto the details of the grand unified physics responsible for their decay.

Big bang nucleosynthesis also turns out to be an important probe of this class of grand unified theories. The understanding of how light elements were synthesized in the furnace of the early universe is one of the great successes of the big bang theory. While most heavy elements are synthesized chiefly in stars, significant production of light elements (e.g., deuterium, helium, lithium) occurred within the first three minutes following the big bang, when temperatures were $T_{BBN} \sim MeV$ . And even though the production (or destruction) of these elements has continued since then, it is possible to look in regions of space where minimal stellar processing takes place. One can compare the observed abundances of elements to the predictions made by theory, which depend sensitively on only one parameter, the ratio of the number of baryons to the number of photons in the universe. The predictions for multiple elemental abundances all agree for a single input—strong evidence for the big bang theory. (The experimental value for this ratio also agrees with a separate determination that comes from detailed measurements of the cosmic microwave background radiation).

However, the agreement for one of the light elements, lithium, is not perfect. As a recent review by Cyburt, Field, and Olive has emphasized [6] observations of both lithium-6 and lithium-7 in low-metallicity stars [7] are somewhat discrepant from the BBN prediction. It is possible that there is misunderstood astrophysics at work—perhaps the measured abundance of lithium is not primordial after all? The other possibility is novel cosmology. For example, if a particle were produced in the big bang with a lifetime of $100$ – $1000 s$ , its decays would be occurring during the crucial epoch of nucleosynthesis. This could shift the predictions for the lithium abundance into accordance with observations [8]. While there are many multiple examples in the literature of such long-lived relic particles with the proper properties to solve the lithium problem, the authors note a lifetime of several minutes—an eternity on particle scales—is particularly elegantly explained if these decays only occur suppressed by powers of the GUT scale.

The lifetime of the relics that modify nucleosynthesis (minutes) and the lifetime of the dark matter ( $10^{19}$ years) could even be explained by the same physics in these theories. Decays during the BBN epoch would result from processes suppressed by the square of the GUT energy, while the decay of the dark matter would correspond to processes suppressed by four powers of the GUT energy.

It will not be easy to determine that GUT-scale physics is the reason for the long lifetime of these relics. The case could be sharpened, however, if the relevant particles are produced at the Large Hadron Collider. If the LHC produces these particles, they could slow down and stop in the detectors there. Their decays could be seen minutes later, a striking signal. The best hope for establishing that one of the GUTs that Arvanitaki et al. discuss is in play is to use a mixture of data from three sources: cosmic rays, colliders, and BBN.

It should be noted that the presence of particles with such long lifetimes is not automatic in just any supersymmetric grand unified theory. Depending on the structure of the theory, the relevant particles could either be absolutely stable, or could have far too short a lifetime to explain either modifications of BBN or cosmic-ray signals. So, Arvanitaki et al. point out structures that ensure that a theory will have particles with lifetimes in the cosmic “sweet spots.” The fact that not all grand unified theories give rise to the relevant decays shows the predictive power of this exploration. So, should the type of signals that Arvanitaki et al. predict be confirmed with upcoming cosmic-ray data (e.g., from the Fermi Gamma Ray Space Telescope), and should the lithium problem sharpen, it will point to a particular class of theories—those with long lived relics, and we may have a chance to learn something about grand unified theories. Hopes of probing GUT-scale physics would no longer solely rest on proton decay.

References

H. Nishino et al., Phys. Rev. Lett. 102, 141801 (2009)
A. Arvanitaki, S. Dimopoulos, S. Dubovsky, P. W. Graham, R. Harnik, and S. Rajendran, Phys. Rev. D 79, 105022 (2009)
H. Goldberg, Phys. Rev. Lett. 50, 1419 (1983)
S. Dimopoulos, S. Raby, and F. Wilczek, Phys. Rev. D 24, 1681 (1981)
O. Adriani et al., Nature 458, 607 (2009); A. A. Abdo et al., Phys. Rev. Lett. 102, 181101 (2009); See also the Viewpoint commentary by B. Winstein and K. Zurek, Physics 2, 37 (2009)
R. H. Cyburt, B. D. Fields, and K. A. Olive, arXiv:0808.2818
F. Spite and M. Spite, Astron. Astrophys. 115, 357 (1982)
S. Bailly, K. Jedamzik, and G. Moultaka, arXiv:0812.0788 (2008)

About the Author

Aaron Pierce is an Assistant Professor of physics at the University of Michigan and member of the Michigan Center for Theoretical Physics. He is a particle theorist and his work focuses on the phenomenology of physics beyond the standard model.