Shining light on iron pnictides with Raman scattering

Miles V. Klein

Viewpoint

Shining light on iron pnictides with Raman scattering

University of Illinois at Urbana-Champaign, 1110 W. Green St., Urbana, IL 61801, USA

June 1, 2009• Physics 2, 46

Calculations of the Raman response for iron pnictide superconductors reveal a collective mode that may be crucial to unravel the pairing symmetry.

Figure caption — **Figure 1:** Simplified Fermi surfaces of Fe-pnictide superconductors (adapted from Fig. 1 of Ref. [13]) showing a pair of pockets at the center of the Brillouin zone with positive superconducting gap and 1/4 of a pocket pair at each of the four symmetry-equivalent zone corners with a negative gap of the same magnitude.

Our theoretical understanding of “classic” one-band superconductors such as simple metals is based on the BCS theory [1], which says that at low temperatures the minimum excitation energy of a single electron (or the energy required to break a Cooper pair) is twice $Δ$ , the superconducting gap. As first shown by Abrikosov and collaborators [2] this is seen in the electronic Raman scattering spectrum, an inelastic light scattering probe, as a continuum that sharply rises from zero at energy shift $2 Δ$ , followed by a fall off at higher energy [3]. The situation is different when a superconductor has multiple conduction bands with different energy gaps, as is the case in the recently discovered $Fe$ -pnictide superconductors. One of the most significant unresolved issues for these materials is the symmetry of the superconducting gap, which in turn is crucially tied to the pairing mechanism. In a recent article published in Physical Review B, Andrey Chubukov of the University of Wisconsin-Madison and Ilya Eremin and Maxim Korshunov from the Max Planck institute for complex systems in Dresden, (hereafter referred to as CEK) have predicted the occurrence of a Raman peak at an energy below $2 Δ$ in the multigap $Fe$ -pnictide compounds where superconductivity is proposed to result from a novel magnetic mechanism [4]. In the absence of disorder, the existence of the Raman peak in the energy gap would signify a collective mode having an infinite lifetime. Since the collective mode occurs only for a particular pairing symmetry, Raman scattering may provide a way to unambiguously distinguish between various superconducting gap symmetries proposed for these materials.

In the past, theorists have predicted collective modes in superconductors in the form of “excitons” in classic superconductors [5] and others have shown how they could be seen using electronic Raman scattering [6,7]. In an extension of BCS theory, Leggett pointed out that a two-band superconductor could have a different type of collective mode. On the superconducting condensate in each band would be superimposed a density wave with a small wave vector $q$ . Such a density wave, a particle-particle (p-p) excitation, would have amplitudes of opposite signs in the two bands so that there would be no net density wave in the sample. For Leggett’s mode to exist, the interband pairing potential must be nonzero and negative but not too negative to keep the mode energy below the single-electron continuum of both bands. In other words, the mode energy must be less than either of the two 2 $Δ$ ’s.

By manipulating the directions of the polarization vectors of the incident and scattered photons in a Raman experiment, it is possible to determine the symmetry of an excitation [3]. In the $q = 0$ limit, Leggett’s collective mode would have the full symmetry, $A_{1 g}$ , of the point group of the sample [8]. The same is true of the mode predicted by CEK. However, the mechanisms responsible for the modes are different.

Raman scattering is a photon in/photon out process that in a metal produces a virtual interband absorption of the incoming photon followed by emission of the outgoing photon. This process excites an electron from an occupied state below the Fermi energy to an empty state above and is therefore a particle-hole (p-h) excitation. In a clean system, the differences in wave vectors $q$ and energy $ħ$ $ω$ of these two states are equal to those of the two photons. The electron spin remains the same. The net effect of these individual excitations occurring throughout the band is a perturbation $H^{'}$ in the form of an electron density wave with wave vector $q$ and energy $ħ$ $ω$ .

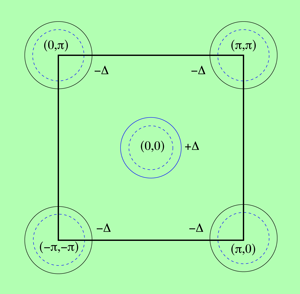
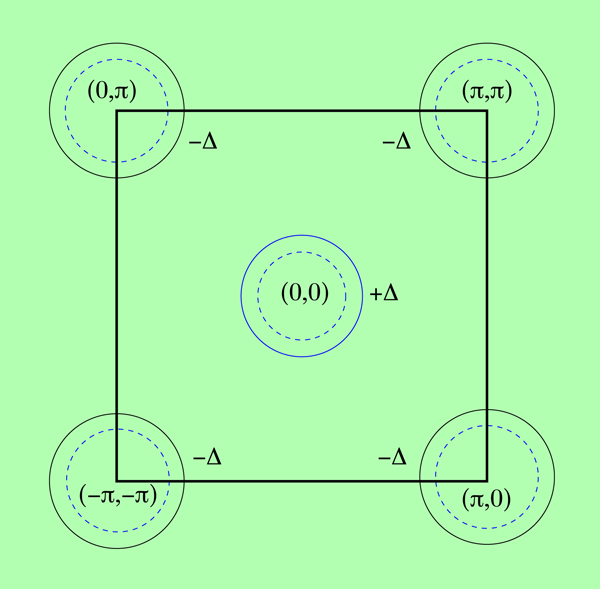
For sufficiently low energy of the photons (below optically allowed interband transitions), the strength of this density wave in a band is proportional to its inverse effective mass $(1 / m^{*})$ . The simplified model of electronic band structure for the $Fe$ -pnictides used by CEK consists of a pair of pockets at the center of the Brillouin zone with positive $m^{*}$ and 1/4 of a pocket pair at each of the four symmetry-equivalent zone corners with negative $m^{*}$ (see Fig. 1). As a simplification, it is assumed that each pocket in a pair shares the same $m^{*}$ and gap values and the combined average is zero [9]. Thus Raman experiments in $A_{1 g}$ symmetry would excite p-h density waves of opposite signs in the two bands. Moreover, the layered nature of the $Fe$ -pnictides allows one to go to the $q = 0$ limit as long as $q$ is perpendicular to the layers, the usual case experimentally [10].

It is a property of the BCS theory that in the superconducting state each p-h density wave automatically turns into a superposition of p-h and p-p density waves. If this were the end of the story, the overall response function would be the sum of the diagonal elements of a $2 \times 2$ matrix on the band indices and no collective mode could result. However, there is more to the story. Roughly speaking, the perturbation $H^{'}$ responsible for Raman scattering “breaks a pair” but the resulting particles continue to interact. CEK consider three types of residual interaction: $V^{(p)},$ $V^{(v)}$ , and $V^{(b)}$ . The first interaction $V^{(p)}$ is of the p-p type and is responsible for the two-band superconducting state (negative for phonon-mediated superconductivity [11]), while $V^{(v)}$ describes a p-h vertex correction. Ordinarily, these two would be identical [12]. The third interaction $V^{(b)}$ is a bubble correction that links the response function “bubble diagrams” forming an infinite series that can be summed.

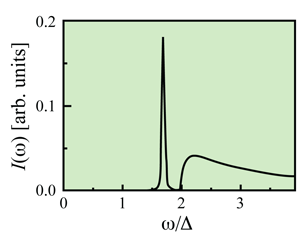
The $Fe$ -pnictides are far from being ordinary metals. They undergo a commensurate antiferromagnetic transition at a temperature well above the superconducting transition temperature. There is theoretical and experimental evidence that the superconductivity in these materials is caused by magnetic fluctuations rather than lattice vibrations. There is also theoretical evidence that the superconducting gap $Δ$ has $A_{1 g}$ symmetry under the point group with a nearly constant value in the electron pockets at the center of the Brillouin zone ( $Δ (k = 0) = Δ$ ) and a nearly constant, but opposite, value in the four pairs of hole pockets—equivalent by symmetry—at the zone corner ( $Δ (π, π) = - Δ$ ) (see Fig. 1). In an earlier paper, the authors of the CEK paper analyzed the antiferromagnetism and superconductivity on an even footing and studied the renormalization flow of the effective interactions represented by the $V^{(p)}$ , $V^{(v)}$ , and $V^{(b)}$ as a function of energy, $ħ$ $ω$ [13]. In Ref. [4], CEK find that the most dominant contribution emerges from the effective interband interaction to produce a resonance below 2 $Δ$ in the $A_{1 g}$ Raman response (see Fig. 2), even if the intraband Coulomb repulsion is the largest term in the Hamiltonian. An $A_{1 g}$ (or equivalently an extended $s$ -wave symmetry $Δ (k) = cos (k_{x}) + cos (k_{y})$ ) pairing gap changes sign between hole and electron pockets but has no nodes along the Fermi surface, as shown in Fig. 1. No collective mode develops for a pure $s$ -wave gap, a $d$ -wave gap, and an extended $s$ -wave gap with $Δ (k) = Δ cos ((k x) / 2) cos ((k y) / 2)$ .

This is figuratively orthogonal to the model employed by Leggett [11], which includes only residual pairing interactions within the “bubble diagrams,” or the modified Leggett model used to explain Raman data in ${MgB}_{2}$ by G. Blumberg and collaborators [14], which includes both residual pairing and vertex interactions, but no “bubble diagram” corrections. It would be exciting if a sub- $2 Δ$ peak could be found in $A_{1 g}$ symmetry Raman experiments on the $Fe$ -pnictides, and it certainly would lend credibility to the scenarios set out by Chubukov, Eremin, and Korshunov.

References

J. Bardeen, L. N. Cooper, and J. R. Schrieffer, Phys. Rev. 108, 1175 (1957)
A. A. Abrikosov and L. A. Fal’kovskii, Zh. Eksp. Teor. Fiz. 40, 262 (1961); [Sov. Phys. - JETP 12, 179 (1961)]; A. A. Abrikosov and V. M. Genkin, Zh. Eksp. Teor. Fiz. 65, 842 (1973); [Sov. Phys. - JETP 38, 417 (1974)]
For a review see: T. P. Devereaux and R. Hackl, Rev. Mod. Phys. 79, 175 (2007)
A. V. Chubukov, I. Eremin, and M. M. Korshunov, Phys. Rev. B 79, 220501 (2009)
A. Bardasis and J. R. Schrieffer, Phys. Rev. 121, 1050 (1961)
M. V. Klein and S. D. Dierker, Phys. Rev. B 29, 4976 (1984)
H. Monien and A. Zawadowski, Phys. Rev. B 41, 8798 (1990)
In the multiband (de facto two band) superconductor ${MgB}_{2}$ this mode has been seen in $A_{1 g}$ symmetry using electronic Raman scattering [14]. In this case, however, the interband pairing potential is too strong, and the mode appears as a resonance about halfway between the two different values of $2 Δ$
A nonzero average can be shown not to couple to CEK’s or Leggett’s collective mode
In ${MgB}_{2}$ the two bands also have opposite signs for $1 / m^{*}$ , and the experiments using near-infrared laser light were in the effective mass limit [14]
A. J. Leggett, Prog. Theor. Phys. 36, 901 (1966)
$V^{(p)}$ and $V^{(v)}$ were both considered in the paper on ${MgB}_{2}$ , and they were assumed to be the same. See Ref. [14]
Andrey V. Chubukov, Maxim M. Korshunov, and Ilya Eremin, Phys. Rev. B 78, 134512 (2008)
G. Blumberg, A. Mialitsin, B. S. Dennis, M. V. Klein, N. D. Zhigadlo, and J. Karpinski, Phys. Rev. Lett. 99, 227002 (2007)

About the Author

Miles V. Klein received his Ph.D. in Physics from Cornell University in 1961. He spent 1961 as a NSF Postdoctoral Fellow at the Max Planck Institute for Metal Research in Stuttgart, Germany and has been on the faculty of the University of Illinois at Urbana-Champaign since 1962. He is best known for his experimental and theoretical work on Raman (inelastic light) scattering from impurity modes in insulators, from semiconductors and from metals, including superconductors. He won the American Physical Society’s Frank Isakson Prize for Optical Effects in Solids in 1990 and is a Fellow of the APS, the American Association for the Advancement of Science, and the American Academy of Arts and Sciences. He is a member of the National Academy of Sciences and was named an Outstanding Referee by the American Physical Society.