Swimming in the Fermi sea

Frédéric Chevy

Viewpoint

Swimming in the Fermi sea

Laboratoire Kastler Brossel, École Normale Supérieure, Paris, France

June 8, 2009• Physics 2, 48

The fermionic analog of a solid-state polaron (an electron surrounded by a cloud of phonons) has been created by dropping a spin-down atom into a Fermi sea of spin-up ultracold atoms.

Figure caption — **Figure 1:** (Top) Experimental scheme of the measurement of the energy of the Fermi polaron. For a free minority atom (left), the resonance condition for a transition between states $| g 〉$ and $| e 〉$ is obtained at a frequency $ν$ . When the atom is immersed in a Fermi sea of majority atoms (right), the energy of $| g 〉$ is modified and the resonance frequency is shifted to a new value $ν'$ . The energy $E$ of the polaron is then simply obtained from $E = h (ν - ν')$ , where $h$ is Planck’s constant. (Bottom) Structure of an imbalanced Fermi cloud. The cloud is organized in concentric shells. The core (pink) is a superfluid with equal spin populations, while the rim (orange) is an ideal gas of majority atoms. The MIT group observes in addition an intermediate normal phase composed of a normal mixture of both spin species (blue).

When one “immerses” a particle in a quantum many-body system, for instance an electron in a solid, the particle “swims” shrouded by a cloud of excitations of its new environment. This composite object is called a quasiparticle and possesses the same features as the initial particle, but with modified physical properties (mass, charge, etc.). As with other many-body phenomena, the ab initio calculation of quasiparticle properties is highly challenging, and in most cases it can only be treated approximately. To overcome this challenge, use of the versatility of laser-cooled gases to simulate many-body condensed matter systems has recently been proposed. Writing in Physical Review Letters [1], André Schirotzek, Cheng-Hsun Wu, Ariel Sommer, and Martin Zwierlein from MIT in the US present a dramatic demonstration of this scheme by studying experimentally the behavior of an atomic impurity immersed in a Fermi sea of ultracold atoms—a very simple system that constitutes the epitome of quasiparticle physics.

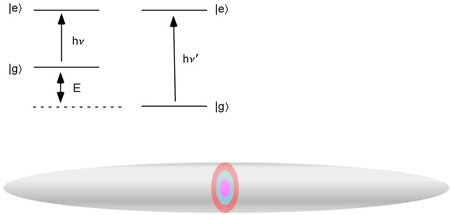
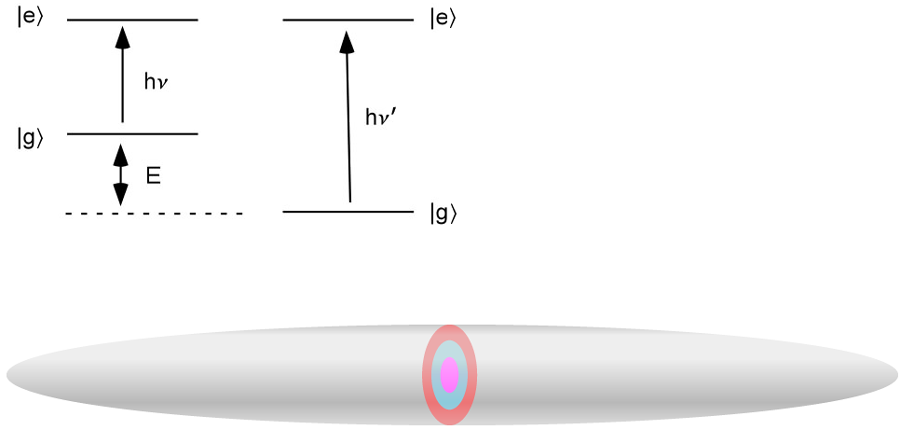
Quasiparticles are very generic features of quantum many-body theories. They are encountered in a wide range of physical systems, from particle physics where the Higgs mechanism suggests that within the Standard Model fundamental particles get a mass by wrapping themselves with excitations of the so-called Higgs field, to solid-state physics where, according to Landau’s Fermi liquid theory, electrons surrounded by particle-hole pairs behave like free electrons with a modified effective mass. The experiment presented in Ref. [1] constitutes a fermionic version of the solid-state physics polaron, an electron coupled to the sea of noninteracting phonons. Indeed, using spin-1/2 lithium atoms, they immerse a spin-down “impurity” atom into a Fermi sea of spin-up atoms, forming a quasiparticle known as a Fermi polaron [2]. The extreme simplicity of their scheme stems from the fact that in cold atom gases, interactions can be safely considered as short ranged, along with the contraint that Pauli’s principle forbids interactions between particles with the same spin. In this system, interactions only take place between spin-up and spin-down atoms, and the Fermi sea can be described as an ideal Fermi gas. By using radiofrequency spectroscopy, the group can readily measure the influence of the Fermi sea on the energy of the impurity. It is obtained very simply by transferring the minority atom from its internal ground state $| g 〉$ to some excited state $| e 〉$ using radiofrequency photons (see Fig. 1). When a spin-down atom is immersed in a Fermi sea of majority atoms, the energy of the ground state is modified, which induces a shift of the absorption lines. Measurement of this shift shows that in the regime of strong interactions, the presence of the Fermi sea decreases the energy of the impurity by $0.6$ $E_{F}$ , where $E_{F}$ is the Fermi energy of the majority Fermi sea, a value in agreement with a simple model, assuming that, despite the strong interactions, the impurity creates only a single particle-hole pair in the Fermi sea [3,4].

More generally, the study presented in Ref. [1] sheds new light on a more general problem, the one related to the fate of a superconductor when the spins of its electrons are all polarized in the same direction, using, for instance, an external magnetic field. It is indeed known that conventional superconductivity arises from pairing electrons of opposite spins. If all particles are polarized in the same spin state, pairing is impossible and no superfluid is expected. Chandrasekhar and Clogston suggested in the1960s that this competition between polarization and pairing leads to an abrupt transition: Below some critical magnetic field, it is energetically too costly to break pairs and the populations of the two spin states remain equal. Above this critical field, Cooper pairs break up and the system begins to polarize, turning the superconductor into a normal metal. Despite its simplicity, this scenario could not be tested with electrons, simply because magnetic fields are expelled from superconductors as a consequence of the Meissner effect. This explains why the Clogston-Chandrasekhar theory was experimentally tested only very recently on ultracold atomic fermions cooled down to superfluidity, done independently at Rice University [5] and MIT, in the group of W. Ketterle [6]. Using laser trapping and cooling techniques, the two groups managed to bring a cloud of strongly interacting lithium atoms with imbalanced spin populations to a temperature lower than one-tenth of the Fermi energy, where superfluidity is expected to occur. Both groups observed that the trapped gas possesses a multishell spin texture, with a rim composed only of atoms of the majority spin (say, spin-up), and a superfluid core with balanced spin-up and spin-down populations (see Fig. 1). The peristence of the superfluid region up to large total spin imbalances proves the robustness of the superfluid state, in agreement with the Clogston-Chandrasekhar scenario. However, while the group at Rice observed only the two phases just described, the MIT team’s results reveal the existence of a third phase, located between the superfluid and pure phases, made up of a nearly ideal gas of Fermi polarons embedded in spin-up atoms [7].

Although the controversy is not yet settled, further theoretical work has demonstrated the strong connection between the Fermi polaron’s energy and the stability of an intermediate partially spin-polarized phase, such as the one observed at MIT [7]. Indeed, a thermodynamical analysis shows that if the presence of the Fermi sea shifts the energy of the impurity downwards by more than $\sim 0.1$ $E_{F}$ then the intermediate normal phase observed at MIT is thermodynamically stable [8]—a value confirmed by the results of Zwierlein’s group.

This study constitutes a textbook demonstration of the concept of analog simulations of condensed matter, where one uses cold atoms to emulate theoretical models developed to describe the behavior of electrons in solids [9]. Indeed, the experiments of Ref. [1] give quantitative measurements of the physical properties of the Fermi polaron and confirm the quasiparticle hypothesis on the nature of the MIT intermediate phase. Another intriguing issue is the dynamics of the polaron: when swimming along the Fermi sea, the impurity pulls behind it a cloud of particle-hole excitations that increases its mass. Theoretical calculations predict a rather mild increase of the mass, which should be confirmed in future experiments. Finally, the MIT-Rice controversy is not yet settled and further work will be necessary to fully understand the discrepancy between the two experiments.

References

A. Schirotzek, C-H. Wu, A. Sommer, and M. W. Zwierlein, Phys. Rev. Lett. 102, 230402 (2009)
N. Prokof’ev and B. Svistunov, Phys. Rev. B 77, 020408 (2008)
R. Combescot, A. Recati, C. Lobo, and F. Chevy, Phys. Rev. Lett. 98, 180402 (2007)
R. Combescot and S. Giraud, Phys. Rev. Lett. 101, 050404 (2008)
G. B. Partridge, W. Li, R. I. Kamar, Y. Liao, and R. G. Hulet, Science 311, 503 (2006)
M. W. Zwierlein, A. Schirotzek, C. H. Schunck, and W. Ketterle, Science 311, 492 (2006)
C. Lobo, A. Recati, S. Giorgini, and S. Stringari, Phys. Rev. Lett. 97, 200403 (2006)
A. Bulgac and M. McNeil Forbes, Phys. Rev. A 75, 031605 (2007)
I. Bloch, J. Dalibard, and W. Zwerger, Rev. Mod. Phys. 80, 885 (2008)

About the Author

Frédéric Chevy is professor at the École Normale Supérieure in Paris. He studies the dynamics of quantum as well as classical fluids, and his latest research involves the study of strongly interacting Bose gases and of mixtures of bosonic and fermionic superfluids.